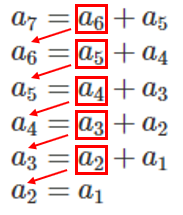ナップサック問題の解法 for Python

ナップサック問題

ナップサック問題をPythonで解いてみた。

問題は下記リンクから参照してください。
https://atcoder.jp/contests/abc032/tasks/abc032_d

ナップサック問題はよくある問題で以下の通り。

$N$個の荷物があり、荷物$i$は重さ$w[i]$、価値$v[i]$とする。許容重量が$W$で、許容重量を超えず、かつ価値が最大になるような荷物の選択をする。

DPのメリット(フィボナッチ数列)

このナップサック問題の解法のポイントは、全てのパターンを計算せず前回の計算結果を使いまわそうということだ。これは、ナップサック問題だけの話ではなく、動的計画法（DP）で共通しており前回までの結果を使いまわして計算をしている。前回の計算結果を使い回し？当たり前じゃんと思うがこれが案外難しい。フィボナッチ数列を例に見ていく。

まずフィボナッチ数列は以下のようになっている。

1, 1, 2, 3, 5, 8, 13, 21 …

a_1 = a_2 = 1

a_{n+2} = a_{n+1} + a_n (a \geqq 1)

フィボナッチ数列の$a_8$を計算する場合、DPを使わなかった場合だとこんな感じ。

$a_8 = a_7 + a_6$

$a_7$を求める

$a_6$を求める

これをもとの式に代入する。
$a_8 = a_7 + a_6$

この$a_7$を求めるときに$a_6$以下を再度計算しているが、この処理は重複しているので無駄。$a_6$の計算結果を$a_7$の$a_6$に代入したら、計算式はだいぶ楽になりますよね？ただ、$a_6$を使い回すのは簡単そうに見えるが、$a_5$、$a_4$、、、と使い回しをしないといけない。
DPを使用すると、この$a_7$を計算するときに$a_6$の結果を再利用できるので、その分計算処理が省け、レスポンスだったりメモリ消費を抑えることができるみたいなメリットがある。（他にも漸化式に近い形でプログラムが組めるので分かりやすい）

話をナップサック問題に戻して、とりあえず漸化式を見てみよう。

漸化式

$$
dp[i+1][j] = max(dp[i][j],dp[i][j-w[i]]+v[i])
$$

$dp[i+1][j]$では先行して$i$+1に記録している。そのため、$dp[i][j]$は$w_i$で前回記録された結果が参照される。dp[i][j-w[i]]+v[i]は今回の荷物の価値とそれ以外に入っている荷物の価値の合計である。

実装

N = 3  # 荷物の数
W = 10  # ナップサックの許容量
w = [9, 6, 4] # 荷物それぞれの重さの配列
v = [15, 10, 6] # 荷物それぞれの価値の配列

# 次使用する配列に今回の結果を残すので+1している
dp = [[0]*(W+1) for i in range(N+1)] # DPの配列作成

for i in range(N):
    for j in range(W+1):
        if j < w[i]: # この時点では許容量を超えていないので選択しない
            dp[i+1][j] = dp[i][j] # ただ選択はしていないが、今回の情報をそのままi+1の方へ移す
        else:
            dp[i+1][j] = max(dp[i][j], dp[i][j-w[i]]+v[i])

print(dp[N][W])

出力結果として16が出力されたら成功。
つまり、重さが6+4=10になり、価値が10+6=16となる。