RankNetを実装してランキング学習

はじめに

ニューラルネットワークでランキング学習するRankNet¹の論文を読み、実装しました。
古い論文ですがアイデアがシンプルでわかりやすく、実装も比較的簡単です。
コードはGitHubにあります。

RankNet

ランキング学習は、データ同士の相対的な順序関係を学習するための方法です。
身近な例だと検索結果の順位付けなどに使われています。

ランキング学習をしたい状況では多くの場合、すべてのデータの絶対的なランキングに関する情報はありません。
そのため、RankNetではランダムに2つのデータをサンプリングし、それらの間の相対的な順序関係を学習します。（任意の2つのデータの順序関係は分かるものとします）
これを繰り返すことで最終的には全体的にも整合の取れた順序関係が獲得されます。

RankNetでは、データを入力すると1つの実数を出力する構造のネットワークを使います。
つまり、データの集合を $\mathcal{X}={ \mathbf{x}_1, \ldots, \mathbf{x}_N }$ 、ニューラルネットワークの入出力関係を $f$ で表現すると、

f: \mathcal{X}\to \mathbb{R}

ということになります。
この出力値（スコア）がランクの高いデータに対しては大きく、低いデータに対しては小さくなるように学習するのがRankNetの基本的な考え方です。

つまり、2つのデータ $\mathbf{x}_i, \mathbf{x}_j$ が与えられた時、「$\mathbf{x}_i$ の方が $\mathbf{x}_j$ よりランクが高い」とは $f(\mathbf{x}_i) > f(\mathbf{x}_j)$ となることです。
これを $\mathbf{x}_i \triangleright \mathbf{x}_j$ と表記します。

具体的には、一方が他方よりもランクが高くなる確率を考え、分類タスクのように学習します。

2つのデータのスコア差を

o_{ij}=f(\mathbf{x}_i)-f(\mathbf{x}_j)

とし、 $\mathbf{x}_i \triangleright \mathbf{x}_j$ となる確率をシグモイド関数を用いて

P_{ij} = P(\mathbf{x}_i \triangleright \mathbf{x}_j) = \frac{1}{1+\exp (-o_{ij})} ~~\cdots(\star)

と表現します。
真の確率を$\bar{P}_{ij}$とすると、2つのデータのスコアリングに関する損失はクロスエントロピーを用いて

C_{ij} = -\bar{P}_{ij} \log P_{ij} -(1-\bar{P}_{ij}) \log (1-P_{ij})

となります。
ここで、$P_{ij}$ が $(\star)$ のようにシグモイド関数で表現されていることを利用すると、

\begin{align*}
C_{ij} &= -\bar{P}_{ij}\log \frac{1}{1+\exp(-o_{ij})} -(1-\bar{P}_{ij})\log \frac{\exp(-o_{ij})}{1+\exp(-o_ij)} \\
&= -\bar{P}_{ij}\log \frac{\exp(o)}{1+\exp(o)}-(1-\bar{P}_{ij})\log \frac{1}{1+\exp(o)} \\
&= -\bar{P}_{ij}\left\{ o_{ij}-\log(1+\exp(o_{ij})) \right\} + (1-\bar{P}_{ij})\log (1+\exp (o_{ij})) \\
&= -\bar{P}_{ij}o_{ij}+\log(1+\exp(o_{ij})) \\
&= -\bar{P}_{ij}o_{ij}+{\rm softplus}(o_{ij})
\end{align*}

と変形できます。
ここで、真の確率 $\bar{P}_{ij}$ は、

\bar{P}_{ij}=
\begin{cases}
1 & \text{if $\mathbf{x}_i \triangleright \mathbf{x}_j$} \\
0 & \text{if $\mathbf{x}_j \triangleright \mathbf{x}_i$} \\
1/2 & \text{otherwise}
\end{cases}

です。

上記の損失関数を通常の分類タスクのように勾配降下法で最適化します。

実験

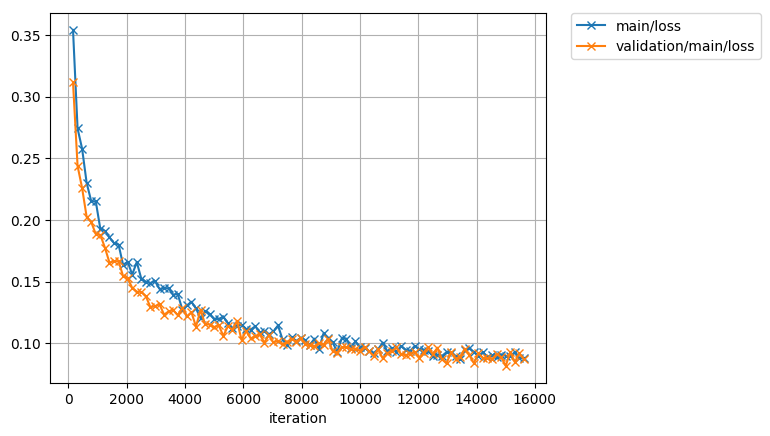
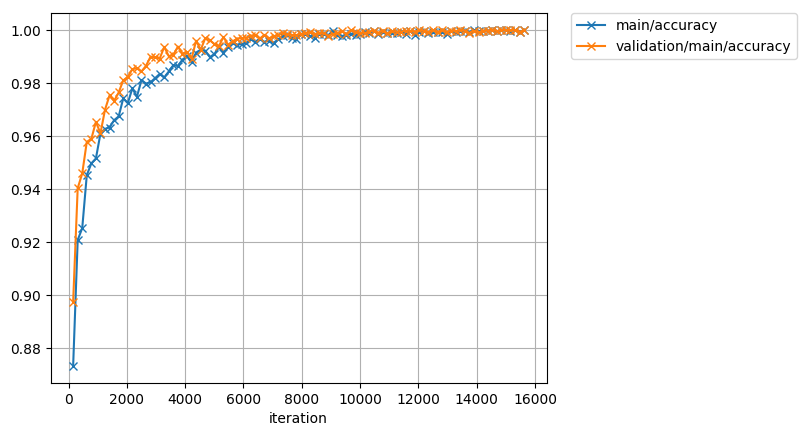
MNISTの手書き数字画像から、順序関係のラベルのみで数字の通りの順序関係を学習してみました。
実装はChainerで行いました。コードはGitHubにあります。

結果

損失と正解率の推移は以下のようになりました。

最終的にはテストデータに対しても100%に近い正解率が出ています。
（ランダムにピックアップした2枚のペアに対して正しく数字の大小を判定できたかどうかで算出しました）

また、各テストデータに対してスコアを算出し、数字ごとに色分けしてヒストグラムにしてみました。

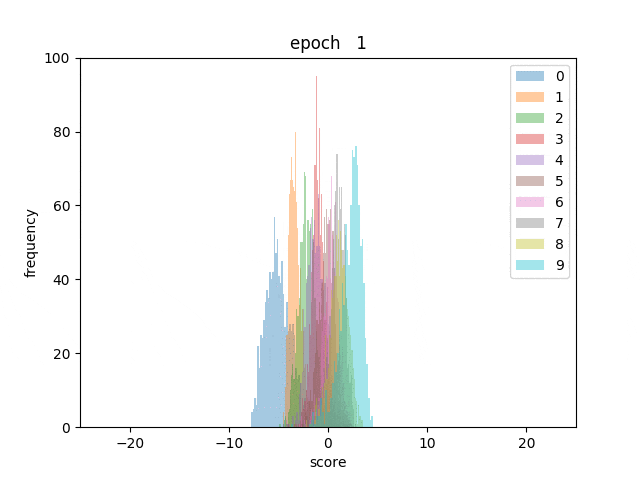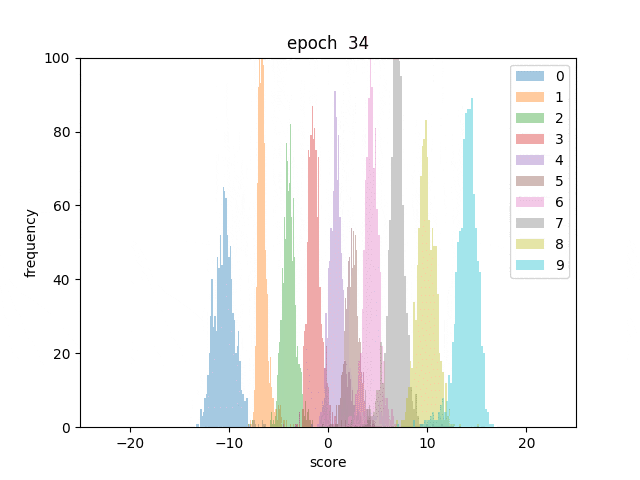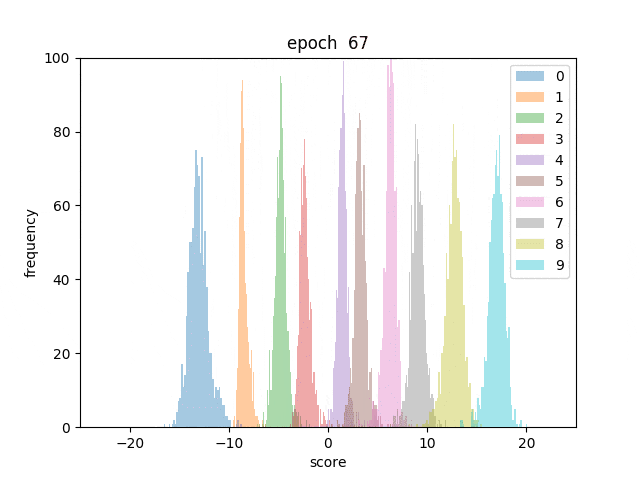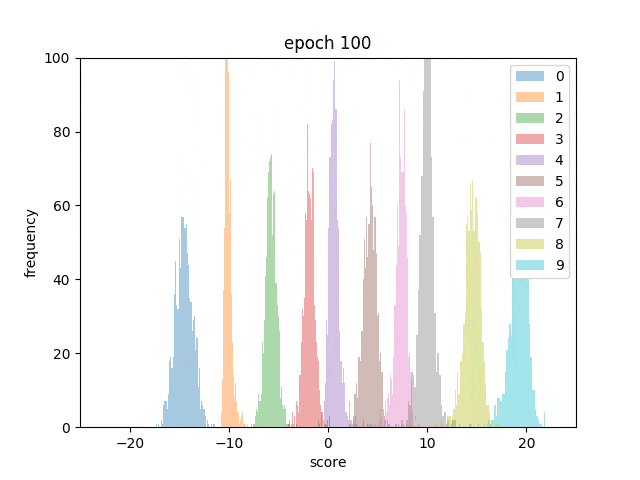
最初は数字が混ざっていますが、学習が進むとはっきりと順序通りに分かれていく様子が分かります。

おわりに

ニューラルネットワークでランキング学習する基本となる手法を紹介しました。
今回紹介した手法はペア同士の順序関係を学習していくものですが、並びのわかっている3つ以上のリストの順序を直接学習できるListNet²などの発展手法もあるので勉強したいと思います。

1. Burges, Christopher, et al. "Learning to rank using gradient descent." Proceedings of the 22nd International Conference on Machine learning (ICML-05). 2005. ↩

2. Cao, Zhe, et al. "Learning to rank: from pairwise approach to listwise approach." Proceedings of the 24th international conference on Machine learning. ACM, 2007. ↩