Zcashのzk-SNARKsの説明を読んだメモ。
その後、これはピノキオと呼ばれるものだと分かった。
Part I: Homomorphic Hiding (HH)
HH $E(x)$ とは以下を満たすもの:
- $E(x)$ から $x$ を見つけるのが困難
- $x \ne y$ であれば、 $E(x) \ne E(y)$
- $E(x)$ と $E(y)$ から、$E(x+y)$などの、$x$ と $y$ を使った数式のHHが作成可能
Part II: Blind Evaluation of Polynomials
使用する体
加算と乗算が可能な、位数 $p$ の体 $F_p$ を使う。
体の加算の記法の追加
ここから、$g^{\alpha}$を、$\alpha \cdot g$と書いてもいいこととする。
多項式
$F_p$ 上の $d$ 次の多項式は、$a_0, a_1, \cdots, a_d \in F_p$ として、
$P(X) = a_0 + a_1\cdot X + a_2 \cdot X^2 + \cdots + a_d \cdot X^d$ for
多項式の評価
$s \in F_p$ を使って $P$ を評価する
$P(s) = a_0 + a_1\cdot s + a_2 \cdot s^2 + \cdots + a_d \cdot s^d$
使用する HH
$E(x)=g^x$
$g$は加算が可能な巡回群のジェネレーター。
以下のように線型結合も可能。
$E(ax+by) = g^{ax+by} = g^{ax} \cdot g^{by} = (g^{x})^a \cdot (g^{y})^b = E(x)^a \cdot E(y)^b$
多項式の秘匿評価
- Alice が $d$ 次の多項式 $P$ を持っている
- Bobがランダムに選んだ $s \in F-P$ 持っている
- Bobは $E(P(s))$ を知りたい。
条件
- Bob が $P$ を知ることがない
- Alice が $s$ を知ることがない
秘匿評価は、以下の形で実現できる
- Bob が Alice に $E(1),E(s), \cdots, E(s^d)$ を送る
- Alice は Bob が送ったデーターを使って $E(P(s))$ を計算して、Bobに送る
2でのAliceの計算の詳細
$E(P(s)) = g^{a_0 + a_1\cdot s + a_2 \cdot s^2 + \cdots + a_d \cdot s^d}$
$= g^{a_0} \cdot g^{a_1 \cdot s} \cdot g^{a_2 \cdot s^2} \cdot \cdots \cdot g^{a_d \cdot s^d}$
$= g^{1 \cdot a_0} \cdot g^{s \cdot a_1} \cdot g^{s^2 \cdot a_2} \cdot \cdots \cdot g^{s^d \cdot a_d}$
$= E(1)^{a_0} \cdot E(s)^{a_1} \cdot E(s^2)^{a_2} \cdot \cdots \cdot E(s^d)^{a_d}$
ここで、Bob が送ったデーターで $E(1), \cdots, E(s_d)$ を置き換える。
Part III: The Knowledge of Coefficient and Assumption
秘匿評価では、Alice が $E(P(s))$ を返す保証がないので、正しい値を返すことを強制するための手段が必要になる。
Knowledge of Coefficient Test
$\alpha \in F_p^$, $b=\alpha \cdot a$ を満たす$(a,b) \in G$ を $\alpha$ペアと呼ぶことにして、以下を行うのが KC Test。($G$ は、$g$がジェネレーターの群。$F_p^$ は、$F_p$からゼロを除いたもの)
- Bob は、$\alpha \in F_p^*$ と $a \in G$ を選択して、 $b=\alpha \cdot a$ を計算する
- Bob が Alice に $\alpha$ペア $(a,b)$ を送る。
- Alice は Bobに、別の $\alpha$ペア $(a',b')$ を送る。
- Bob は、 $(a',b')$ が $\alpha$ペア $(a',b')$ であれば受け入れる。(Bob は $\alpha$ を知っているので、$b'=\alpha \cdot 'a$ で簡単に検証できる)
Knowledge of Coefficient Assumption
Alice の $\alpha$ についての知識は $\alpha \cdot a$ のみで、$G$ 上でここから $\alpha$ を逆算することは、離散対数問題を解くことになるのでできないが、$\gamma \in F_p^*$ をランダムに選んで、$(\gamma \cdot a', \gamma \cdot b')$ とすることで、 $\alpha$ペアになる $(a',b')$ を作ることができる。
理由は、
$b'=\gamma \cdot b = \gamma \cdot \alpha \cdot a = \alpha(\gamma \cdot a) = \alpha \cdot a'$
Alice はこの形でしか正しい $(a',b')$ を返すことができないので、正しい$(a',b')$を返せた場合には、$\gamma$ を知っていることになる。これを、Knowledge of Coefficient Assumption (KCA) と呼ぶ、
Part IV: How to make Blind Evaluation of Polynomials Verifiable
検証可能な多項式の秘匿評価
秘匿評価では、Alice が Bob に $E(P(s))$ を返す保証がなかったが、Knowledge of Coefficient Assumption を拡張したものを使って、その保証をつけていく。
拡張 Knowledge of Coefficient Assumption
- Bob は、$\alpha \in F_p^*$ と $a \in G$ を選択して、 $b=\alpha \cdot a$ を計算する
- Bob が Alice に $\alpha$ペア $(a,b)$ を「複数」送る。
- Alice は Bobに、別の $\alpha$ペア $(a',b')$ を、「複数の$\alpha$ペア $(a,b)$」 から作って、送る。
- Bob は、 $(a',b')$ が $\alpha$ペア $(a',b')$ であれば受け入れる。
複数のαペアから、一つの新しいαペアを作る方法
たとえば、2つの $\alpha$ペア、$(a_1,b_1), (a_2,b_2)$ から作る場合は、$c_1,c_2 \in F_p$ をランダムに選んで、
$(a',b')=(c_1 \cdot a_1 + c_2 \cdot a_2, c_1 \cdot b_1 + c_2 \cdot b_2)$ のようにする。
これが $\alpha$ ペアになる理由は、
$b'= c_1 \cdot b_1 + c_2 \cdot b_2 = c_1 \cdot \alpha \cdot a_1 + c_2 \cdot \alpha \cdot a_2 = \alpha (c_1 \cdot a_1 + c_2 \cdot a_2) = \alpha \cdot a'$
より一般的には、
$(a',b') = (\sum_{i=1}^{d}{c_ia_i}, \sum_{i=1}^{d}{c_ib_i}) $
拡張KCAが言っていること
Alice が正しい $(a',b')$ を返した場合には、Alice はa` $a'$ と $a_1, \cdots, a_d$ の線形関係を知っている。言い方を変えると、$a' = c_1 \cdot a_1 + \cdots + c_d \cdot a_d$ となるような、$c_1, \cdots, c_d$ を知っている。
d-power Knowledge of Coefficient Assumption (d-KCA)
Bob が $\alpha \in F_p^*$ と $s \in F_p$ をランダムに選んで、Alice に $(g, \alpha \cdot g),(s \cdot g, \alpha s \cdot g), \cdots, (s^d \cdot g, \alpha s^d \cdot g)$ 送ると仮定する。
また、Alice が別の $\alpha$ペアをBobに送り返すと仮定すると、無視できる確率を除いて、Alice は $\sum_{i=0}^d{c_is^i \cdot g} = a'$ となるような $c_0, \cdots, c_d \in F_p$ を知っている。
検証可能な秘匿評価プロトコル
前提となるHH
$E(x)=g^x=x \cdot g$
- Bob が $\alpha \in F_p^*$ と $s \in F_p$ をランダムに選んで、Alice に $1,s,s^2,\cdots,s^d$ の HHと、 $\alpha,\alpha \cdot s,\alpha \cdot s^2,\cdots,\alpha \cdot s^d$ の HH を送る。
- Alice は、$a=P(s) \cdot g$ とは、$b= \alpha P(s) \cdot g$ を、Bob から送られたデーターを使って計算して、Bob に返す。
- Bob は $b = \alpha \cdot a$ が成立していれば、受け入れる。
Alice が 2 を計算可能な理由
$P(s)\cdot g = g^{P(s)} = g^{c_0 + c_1 \cdot s + \cdots + c_1 \cdot s^d} = g^{c_0} \cdot g^{c_1 \cdot s} \cdot \cdots \cdot g^{c_1 \cdot s^d} = g^{1 \cdot c_0} \cdot g^{s \cdot c_1} \cdot \cdots \cdot g^{s^d \cdot c_1} = E(1)^{c_0} \cdot E(s)^{c_1} \cdot \cdots \cdot E(s^d)^{c_1} $
$\alpha \cdot P(s)\cdot g$ についても同様。
##### d-KCAの適用
多項式 $P$ の各項の係数を $c_0, \cdots, c_d \in F_p$、Bob の送る2種類の HH を 次数でグループ分けしたものを $\alpha$ペアの集合と考えると、d-KCA を適用することができる。d-KCA で Alice が知っているとわかるものは、Pなので、Alice が正しい $a,b$ を Bob に返した場合、無視できる確率を除いて、Alice が多項式 P を知っているということができる。
Part V: From Computations to Polynomials
Alice が証明したいこと
Alice が $(c_1 \cdot c+2) \cdot (c_1 + c_3) = 7$ であるような $c_1, c_2, c_3 \in F_p$ を知っていることを Bob に証明したいとする。
算術回路
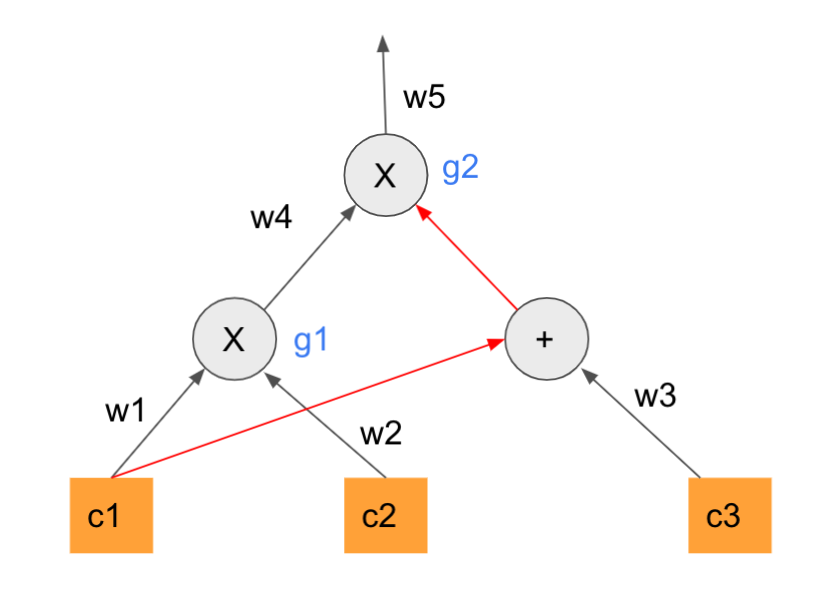
加算ゲートと、乗算ゲート。ゲート間をつなぐワイヤーで構成されている。Alice の証明したいことに対応する算術回路は以下のようになる。
$w1, w2, w3$が入力、$w5$が出力を表している。
作り方のルール
- 2つの以上のゲートに向かうワイヤーは、1つのワイヤーとして考える。例えば、$w1$ は $g1$ と $+$のゲートに向かう1つのワイヤーとして考える。
- 乗算ゲートには、常に2つの入力が存在して、左の入力を、左ワイヤー、右の入力を右ワイヤーと呼ぶ。
- 加算ゲートにはラベルをつけない。
- 加算ゲートから乗算ゲートに向かうワイヤーにはラベルをつけず、加算ゲートの入力が直接乗算ゲートに接続していると考える。上の例では、$g2$の入力は、$w1, w3$になる。
Legal Assignment
乗算ゲートの入力を掛けたものが出力と一致するような、ラベルのついたワイヤーへの値の割り当て。
上の例では、$c_4=c_1 \cdot c_2$、$c_5=c_4 \cdot (c_1 + c_3)$ で、$c_5=7$ となるような $(c_1,c_2,c_3,c_4,c_5)$。
Legal Assignment を使うと、Alice は $c_5=7$ となるような $(c_1,c_2,c_3,c_4,c_5)$ を知っていることを証明したいということになる。
Quadratic Arithmetic Program (QAP)
算術回路をQAPに変換する。
Target Points
まず、それぞれの乗算ゲートに、$1,2,\cdots \in F_p$ を割り当てる。
上の例の場合は、$g1 = 1, g2 = 2$のようになる。
この割り当てられた数値を Target Point と呼ぶ
Li, Ri, Oi 式
次に、Legal Assignmentの数値の数を $m$ として、$L_{1 \cdots m}, R_{1 \cdots m}. O_{1 \cdots m}$ を関連する Target Point で評価した場合に 1 に、その他の値では 0 になるように定義する。
たとえば、上の例の場合は、Target Point が 1 の場合、対応するゲートは $g1$ で、左入力が $w1$、右入力が $w2$ 、$w4$ が出力になっているので、$L_1 = R_2 = O_4 = 2 - X$ とすると、$X=1$ の時には、$L1,R2,O4=1$になり、その他の場合(この例では2のみ)に $0$ になる。
同様に、Target Point が 2 の場合は、対応するゲートは $g2$ で、左入力が $w4$、右入力が $w1,w3$ 、$w5$ が出力になっているので、$L_4 = R_1 = R_3 = O_5 = X - 1$ となる。
その他については 0 を設定する。
${L_i, R_i, O_i} 式は、関連する項を、評価対象にするかを示すフラグとして、この後で使われる。
#### ワイヤーへの割当値と Li, Ri, Oi 式の結合 P
次に、Li, Ri, Oi 式に、関連するワイヤーへの割当値をかけ合わせて、足し上げた値を、$L, R, O$ それぞれに対して、以下のように作る。ワイヤーへの割当値の数を $m$ として、
$L := \sum_{i=1}^{m}{c_i \cdot L_i}$
$R := \sum_{i=1}^{m}{c_i \cdot R_i}$
$O := \sum_{i=1}^{m}{c_i \cdot O_i}$
として、
$P := L \cdot R - O$
P が 0 になる場合
Legal Assignment とは、乗算ゲートの入力を掛けたものが出力と一致するような、 $(c_1, \cdots, c_m)$ への値の割り当てなので、$(c_1, \cdots, c_m)$ が Legal Assignment であれば、 P は 0 になる。
Target Polynomial
多項式 $P(a)$ が $a \in F_p$ で、0 になる場合には、$P(X)$ の因数に $(X-a)$が含まれている ($(a-a)=0$なので)。
なので、全ての Target Point で $P$ が 0 になるためには、全ての Target Point をゼロにする項が全て $P$ に含まれている必要がある。これらの項を集めたものを Target Polynomial と呼ぶ。
上の例の Target Polynomial は、$T(x)=(X-1) \cdot (X-2)$。
QAPの定義
Li, Ri, Oi 式 と、 Target Polynomial が QAP を構成する。
また、値割り当ての結果、TがPを割り切る場合に、その割り当ては QAP を満たすという。
QAPの言い方では、Alice は $c_5=7$ である QAP を満たす値割り当て $(c_1,c_2,c_3,c_4,c_5)$ を知っていることを証明したいということになる。
Part VI: The Pinocchio Protocol
Pinocchio Protocolを使うことで、Alice は、Alice が QAP を満たす割り当てを知っていることを、Bob に対して簡潔に証明することができる。
プロトコルの基礎的な部分
Alice が QAP を満たす割り当てを使って、$L, R, O$ を作り、そこから $P$ を作った場合には、 $P=H \cdot T$ が満たす $H$ が存在する。
逆に、Alice が QAP を満さない割り当てを使って、$L, R, O$ を作った場合には、$T$ は $P$ を割り切らないので、作られた $L,R,O,P$と、$P$ を割ることでできる $H$ は、満たす場合に作られるものとは異なるものになる。
次数
次数を見てみると、$P$の次数は高々 $2(d-1)$。$L,R,O$ の次数は高々$d-1$、$H$ の次数は高々$d-2$ だとわかる。
シュワルツ・ジッペルの補題
シュワルツ・ジッペルの補題によれば、高々次数が $2d$ の2つの異なる多項式間で、共通する点は高々 $2d$ なので、$F_p$ の位数 $p$ を $2d$ と比べて大きくすればするほど、2つの異なる多項式のカーブ上の点は一致しなくなる。
そして、その場合、Alice が QAP を満さない割り当てを使った場合に $P(s)=H(s) \cdot T(s)$ が成り立つ可能性はとても小さくなる。
#### プロトコルのスケッチ
- Alice が、次数が高々 $d$ の多項式 $L,R,O,H$ を選択する
- Bob が、ランダムに $s \in F_p$ を選んで、$E(T(s))$ を計算する
- Alice が、$s$ で $L,R,O,H$ を評価したものの HH を Bob に送る
- Bob が、$s$ で $E(L(s) \cdot R(s) - O(s)) = E(T(s) \cdot H(s))$ が成り立つかを確認する
- Alice が QAP を満さない割り当てを使った場合には、ほとんどの $s$ で等式が成り立たない。
- Alice は $s$ を知ることなく、多項式を選択するためには、検証可能な秘匿評価プロトコルを使うことができる。
このスケッチを、zk-SNARK にするために、4つ言及すべきポイントがある。そのうち2つを、Part VI で扱う。
言及すべきポイント
1. Alice は知っていると主張している値の割り当てをベースに作られた多項式を選択する必要がある
割り当てが QAP を満さないケースの中に、$L \cdot R-O=T \cdot H$ は満たしていても、$L,R,O,H$ を、Alice が知っていると主張している $(c_1, \cdots, c_m)$ を使って、
$L := \sum_{i=1}^{m}{c_i \cdot L_i}$
$R := \sum_{i=1}^{m}{c_i \cdot R_i}$
$O := \sum_{i=1}^{m}{c_i \cdot O_i}$
の形で作っていないというケースがありうる。
Part IV で出て来たプロトコルで作られた $L,R,O,H$ は、$L \cdot R-O=T \cdot H$ を満たすものの、$(c_1, \cdots, c_m)$ から作られることは保証していない。
ここで、係数がぶつからないように、次数を $d$ ずつずらしながら $L, R, O$ 足し上げた $F$ を作る。
$F = L + X^{d+1} \cdot R + X^{2(d-1)} \cdot O$
同様に QAP の $L_i, R_i, O_i$ を結合すると、
$F_i = L_i + X^{d+1} \cdot R_i + X^{2(d-1)} \cdot O_i$
となる。全ての Target Point について $F_i$ を足しあげた場合は、
$F_1 + \cdots + F_m = (L_1 + \cdots + L_m) + X^{d+1} \cdot (R_1 + \cdots + R_m) + X^{2(d-1)} \cdot (O_1 + \cdots + O_m)$
のようになって、$L,R,O$ がそれぞれ別の項に割り振られていくことがわかる。
さらに、$(c_1, \cdots, c_m)$ と $F_i$ を線形結合して $\sum_{i=1}^{m}{c_i \cdot F_i}$ とすると、
$c_i \cdot F_i = c_i \cdot L_i + c_i \cdot X^{d+1} \cdot R_i + c_i \cdot X^{2(d-1)} \cdot O_i$
で、
$F = c_1 \cdot F_1 + \cdots + c_1 \cdot F_m = (c_1 \cdot L_1 + \cdots + c_1 \cdot L_m) + (c_1 \cdot c_2 \cdots \cdot c_m) \cdot X^{d+1} \cdot (c_1 \cdot R_1 + \cdots + c_1 \cdot R_m) + (c_1 \cdot c_2 \cdots \cdot c_m) \cdot X^{2(d-1)} \cdot (c_1 \cdot O_1 + \cdots + c_1 \cdot O_m)$
となって、
$F = L + X^{d+1} \cdot R + X^{2(d-1)} \cdot O$
になることがわかるので、$F$ が $(c_1, \cdots, c_m)$ と $F_i$ の線形結合である場合には、$L,R,O$ が $(c_1, \cdots, c_m)$ から作られたものだと言える。
なので、上で指摘した Part IV で出て来たプロトコルの問題点を補完するには、Bob は Alice に$ F$ が $(c_1, \cdots, c_m)$ と $F_i$ の線形結合かどうかを聞けばよい。これは、検証可能な秘匿評価を使うことで実現できる。
- Bob は $\beta \in F_p^*$ を選択して、Alice に $E(\beta \cdot F_1(s)), \cdots, E(\beta \cdot F_m(s))$ を送る
- Alice は Bob が送ったデーターと、知っていると主張している $(c_1, \cdots, c_m)$ を使って $E(\beta \cdot F(s))$ を計算してBob に送る
- Bob は $E(\beta \cdot F(s)) = E(\beta \cdot F_1(s)), \cdots, E(\beta \cdot F_m(s))$ が成立していれば、受け入れる
このテストが通った場合、拡張 KCA により Alice は $F$ を $F_i, \cdots, F_m$ の線形結合から作る方法を知っていると言える。
2.ゼロ知識部分の追加。値の割り当てを隠す。
zk-SNARKでは、Alice は全ての値の割り当てについての情報を隠したいが、$E(L(s)),E(R(s)),E(O(s)),E(H(s))$は、若干の値の割り当てについての情報を与えてしまう。
例えば、$(c_1', \cdots, c_m')$ の QAP を満たさない値の割り当てを使って、$L',R',O',H'$ と、その HH を計算することができるので、$(c_1', \cdots, c_m')$ が正しい割り当てでないことがわかってしまう。
Alice は T をランダムにシフトすることによって、この情報漏れを防ぐことができる。具体的には、
$\delta_1, \delta_2, \delta_3 \in F_p^*$ をランダムに選んで、
$L_z:=L \cdot \delta_1$
$R_z:=R \cdot \delta_2$
$O_z:=L \cdot \delta_3$
を作り、$L \cdot R - O = T \cdot H$ の $L,R,O$ を $L_z,R_z,O_z$ で置き換えると、
置き換えた式も $T$ で割り切れるので、Bob は受け入れるが、$\delta_1, \delta_2, \delta_3 \in F_p^*$ は $L$ に関係なくランダムに選ばれた値のため、置き換えた式は$L$ とそのもとになっている値の割り当てについて、何も情報を与えない。
Part VII: Parings of Elliptic Curves
楕円曲線とそのペアリング
$p$を3以上の素数として、$4u^3 + 27v^2 \neq 0$ となるような $u,v \in F_p$ を選ぶ。楕円曲線 $C$ は、
$Y^2 = X^3 + u \cdot x + v$
を満たす点の集合になる。
また、$C$ の中で、$(x,y) \in F_p^2$ を満たす点の集合に、無限遠点 $O$ を加えたものを群 $C(F_p)$ として考える。
群の上での加算の定義
Divisor Class Groupから加算を導出する。
Divisor Class Groupの課す制限
直線上の点の合計はゼロ
2点を通る $y$ 軸に対して並行な直線の加算
ある $x$ 座標 $c$ について $X=c$ で、$P=(x_1,y_x)$ とする。曲線の式は $Y^2=f(X)$ なので、$(x_1,y_x)$ が曲線上にある場合は、$(x_1,-y_1)$ も曲線上にあることになり、曲線の$Y$の次数が 2 なので、他の点と直線は交わらない。そして、Divisor Class Group の制約から $P+Q=O$ となる。また、ここから $P=-Q$ が導き出せる。
2点を通る $y$ 軸に対して並行でない直線の加算
次に、曲線上の $x$ 座標の異なる $2$ つの点 $P,Q$ を通る直線を引くと、曲線の$X$の次数は 3 なので、もう一つの点 $R=(x,y)$ でのみ、その直線が曲線と交わる。そして、Divisor Class Group の制約から $P+Q+R=O$ となる。また、ここから $P+Q=-R$ が導き出せる。
加算から乗算
ここから、加算の定義された群 $C(F_p)$ を $G_1$ と呼ぶことにする。また、$G_1$ の位数を $r$ 、またそのジェネレーターを $g$ とする。
Embedding Degree
$p^k-1 \equiv 0 \bmod r$ が成り立つ最小の $k$
曲線の Embedding Degree が小さすぎない場合(例えば $6$)は、離散対数問題を解くことが難しくなる。
G_T
ここで、乗算のできる群 $F_p^k$ は、位数が $r$ の部分群を含んでいて、これを $G_T$ と呼ぶ。$F_p$ で定義した加算と同じ加算を、$F_p^k$ 上で、無限遠点 $O$ と共に定義してできる群を $C(F_p^k)$ と呼ぶ。ここで、$C(F_p^k)$ は $G_1$ を含むことに注意する。また、$C(F_p^k)$ は、また別の、位数 $r$ の部分群 $G_2$ も含んでいる。(実際 $r-1$ のそのような群を含んでいる)。
Tate Reduced Pairing
$G1,G2$のジェネレーターを、$g \in G_1, h \in G_2$ に固定すると、Tate Reduced Pairing を使って、$G1,G2$ の要素を、以下の形で $G_T$に紐付けることができる。
- $G_T$ のジェネレーター $G$ について、$Tate(g,h) = G$
- $a,b \in F_r$ について、$Tate(a \cdot g, b \cdot h) = G^{ab}$
乗算をサポートしたHH
Tate Reduced Pairing を使うことで、
$E_1(x) = x \cdot g$
$E_2(x) = x \cdot h$
$\mathbb{E}(x) = x \cdot G$
と定義して、$E_1(x)$ と $E_2(y)$ から、$\mathbb{E}(xy)$ を計算できる。
CRS を使った非対話的な証明
わかりやすい、最も強力な非対話的な証明は、全く下準備なしに、証明者が1つのメッセージを、全参加者に対してブロードキャストすると、全参加者が証明者の主張が正しいことに付いて納得するというものだが、ほとんどの場合には不可能。
このやり方を若干緩めた方法に、CRS (Common Reference String) がある。CRS では、証明が作られる前に、事前にセットアップ段階を設けて、そこで CRS と呼ばれる文字列を、作られる過程での乱数性がどの参加者にも伝わらないように作り、全ての参加者にブロードキャストする。そしてブロードキャストされた CRS が証明の作成と検証に使われる。
非対話秘匿評価プロトコル
Bobの1つ目のメッセージを CRS で置き換えることで、検証可能な秘匿評価プロトコルを非対話で行うことができる。具体的には以下の通り:
下準備
ランダムに $\alpha \in F_r^*, s \in F_r$ を選択して 以下の CRS をブロードキャストする。
$(E_1(1),E_1(s), \cdots, E_1(s^d),(E_2(\alpha),E_1(\alpha s), \cdots, E_1(\alpha s^d))$
証明
Alice が $a=E_1(P(s))$ と $b=\alpha P(s)$ を CRS と $E_1,E_2$ は線型結合ができることを利用して計算する。
検証
Bob は $a=E_1(x), b=E_2(y)$ となる $x, y \in F_r$ について、$\mathbb{E}(\alpha x)=Tate(E_1(x), E_2(\alpha))$ と $\mathbb{E}(y)=Tate(E_1(1), E_2(y))$ を計算して、$\mathbb{E}(\alpha x)$ と $\mathbb{E}(y)$ が等しいこと確認する。等しければ、$\alpha x = y$ が成り立つことになる。
補足
- $x,y$ を対応する証明での値に置き換えると、$\mathbb{E}(\alpha P(s))=Tate(E_1(P(s)), E_2(\alpha))$ と $\mathbb{E}(\alpha P(s))=Tate(E_1(1), E_2(\alpha P(s)))$ になる。
- $\mathbb{E}(y)$ と $E_2(y)$ は違う体上の値なので、$\mathbb{E}(y)=Tate(E_1(1), E_2(y))$ のように比較する体にマップする必要がある。
検証可能な秘匿評価プロトコルとその秘匿版との比較
| ステップ | 対話版 | 秘匿版 |
|---|---|---|
| 1 | $\alpha \in F_r^*, s \in F_r$をランダムに選ぶ | 同じ |
| 2 | $1,s,\cdots,s^d$ と $\alpha,\alpha s,\cdots,\alpha s^d$ のHHを$E$で作る | $1,s,\cdots,s^d$ の HH を $E_1$で、$\alpha,\alpha s,\cdots,\alpha s^d$ のHHを$E_2$で作る |
| 3 | $a=E(P(s))$ と $b=E(\alpha P(s))$ を計算 | $a=E_1(P(s))$ と $b=E_2(\alpha P(s))$ を計算 |
| 4 | $b=\alpha \cdot a$ を確認 | $a=E_1(x), b=E_2(y)$ となる $x, y \in F_r$ について、$\mathbb{E}(\alpha x)=Tate(E_1(x), E_2(\alpha))$ と $\mathbb{E}(y)=Tate(E_1(1), E_2(y))$ を計算して、$\mathbb{E}(\alpha x)=\mathbb{E}(y)$を確認 |