この記事は古川研究室 Advent Calendar 17日目の記事です．
本記事は古川研究室の学生が学習の一環として書いたものです．内容が曖昧であったり表現が多少異なったりする場合があります．
はじめに
機械学習の手法を勉強していると，いたるところで距離や誤差を測るという手続きに出くわします．大抵の場合，二乗距離という測り方で誤差を測っています．私も最初は「そういうものなのね」と軽く流していたのですが，「学習の”良さ”をどのように定義するか」について考えたり，ノルムや距離の測り方について勉強していく中で，「なんで二乗誤差で測るの？」という疑問が浮かびました．この記事は「なんで二乗誤差で測るの？」という疑問を解決するべく勉強したまとめとなっています．
そもそも二乗誤差とは？
ここでいう二乗誤差とは，データ間の距離を二乗距離によって算出したものを指しています．この二乗距離の値を誤差と定義することが多いため，二乗誤差と呼ばれています．このとき，二乗距離の値と二乗誤差の値は等しいです．
一般に，D次元のベクトルデータ$\mathbf{x}=(x_1,x_2, \cdots ,x_D)^\mathsf{T}$と$\mathbf{y}=(y_1,y_2, \cdots ,y_D)^\mathsf{T}$の二乗距離は次のように計算されます．
$$||\mathbf{x}-\mathbf{y}||^2 = (x_1-y_1)^2 + (x_2-y_2)^2 + \cdots + (x_D-y_D)^2$$
具体例として，$D=2$すなわち2次元ベクトルデータ$\mathbf{x}$，$\mathbf{y}$と二乗距離$||\mathbf{x}-\mathbf{y}||^2$の関係を以下に図示してみました．
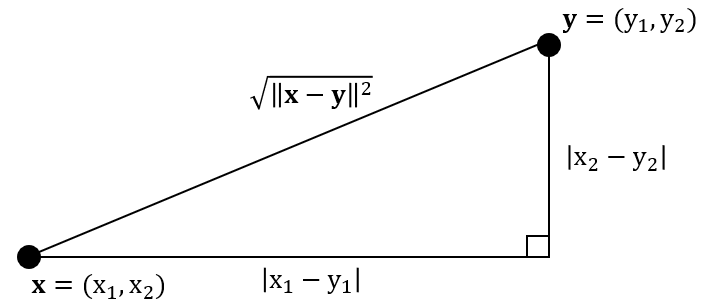
この直角三角形の底辺の長さと高さは，それぞれ$\mathbf{x}$と$\mathbf{y}$における同じ軸の成分の差の絶対値で計算されます．ここで$|x_1-y_1|=\sqrt{(x_1-y_1)^2}$となります．このとき$\mathbf{x}$と$\mathbf{y}$の二乗距離は斜辺の二乗と等しくなります．言い換えると，斜辺は$\mathbf{x}$と$\mathbf{y}$の二乗距離のルートで計算されます（ちなみにこれがユークリッド距離，L2ノルムです）．
二乗誤差で測られている手法
二乗誤差は，機械学習の様々な手法で使われています．ざっと例を挙げてみますと，次のようなものがあります．
- 教師あり回帰より，線形単回帰分析
- 教師あり分類より，2クラス分類（二値関数の近似問題として定式化されたもの）
- 教師なし次元削減より，主成分分析（Principal Component Analysis: PCA）
- クラスタリングより，K-means法（ご存知かと思いますが教師なし学習です）
- 教師なし多様体学習より，自己組織化マップ（Self-Organizing Map: SOM），UKR（Unspervised Kernel Regression）
ここでは各手法については詳しく触れませんが，いずれも学習の過程で二乗距離が用いられています．
私は上の4つは主に[1]で学びました．最後のSOMとUKRについてはそれぞれ[2]，[3]が分かりやすいかと思います．
二乗誤差以外の測り方
誤差や距離の測り方は，二乗距離を用いた測り方だけではありません．
-
ミンコフスキー距離
- L1ノルムはマンハッタン距離や市街地距離などとも呼ばれます．
- L2ノルムはユークリッド距離とも呼ばれます．中学校の数学で距離といえばコレです．
- L∞ノルムはチェビシェフ距離やチェス盤距離などとも呼ばれます．
- データの分散や標準偏差を用いた誤差の定義
他にも，確率分布間の距離を考えようとすると，KL-Divergenceや相互情報量など，エントロピーを導入したものを用いたほうが適切な場合があります．同様に，カテゴリデータ（0/1のベクトルデータ）の場合はハミング距離などを考えたほうが適切かもしれません．
ミンコフスキー距離の具体例，ノルムについては，[4] のページが非常にわかりやすく，参考になりました．
ところで，距離の測り方がいろいろあることは分かりましたが，注意点は測り方だけではありません．実際に「どこの距離を測っているのか」に注意を向けることも大切です．同様に，「何の距離を測っているのか」にも注意を向けるとよいです．
抽象的ですが，以下に例を示します．
- 観測空間における観測データと予測データの距離
- 潜在空間における潜在変数間の距離
- 観測データを写像した非線形空間におけるデータ間の距離
実際に，どのようなデータセットの場合にどのような距離を用いるのが適切かについて考えるときは，[5]のページが参考になるかもしれません．
実際に試してみた
古川研究室の基盤技術であるSOMも二乗距離を用いて学習を行っています．SOMは「観測データは，ある本質的な構造から生成されたものであり，その構造は多様体のかたちをとっているはずだ」という多様体仮説のもと，本質的な構造すなわち潜在変数と潜在空間から観測空間への写像を推定します．
詳細な説明は[2]古川研究室のSOMドキュメントに譲ります．
今回は，もともとSOMで使われている二乗距離の部分をユークリッド距離に置き換えて学習した結果と，二乗距離のままのSOMの学習結果を比較してみます．以下に示しているgifは，一枚目が二乗距離のまま学習したSOM，二枚目がユークリッド距離に置き換えて学習したSOMです．
各gifの左側が3次元の観測空間，右側が2次元の潜在空間です．観測空間上の観測データに対して，潜在空間上の潜在変数と潜在空間から観測空間への位相保存写像を学習します．観測空間に描画される網目構造は学習した多様体を表しています．
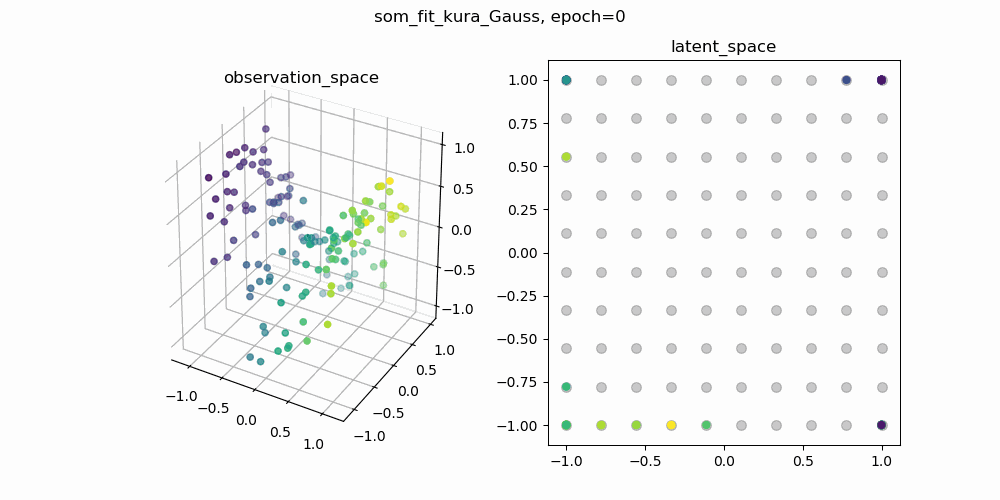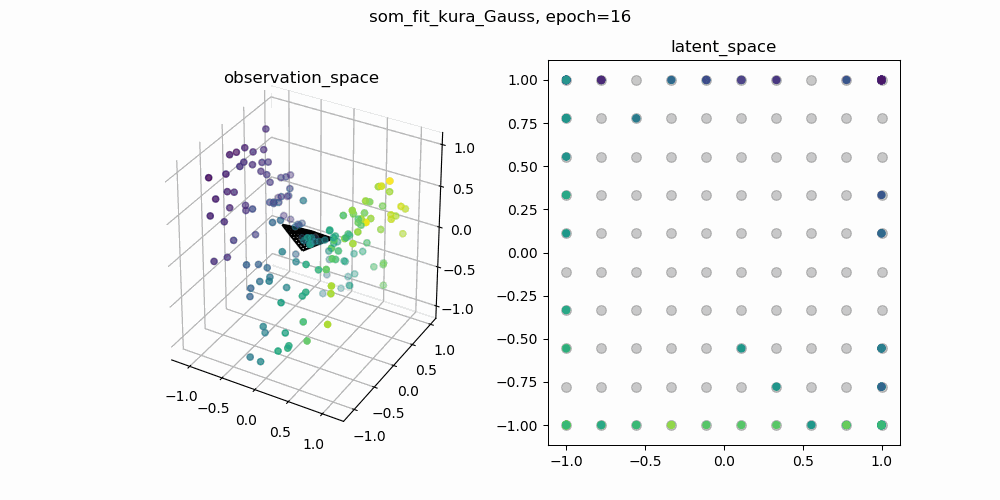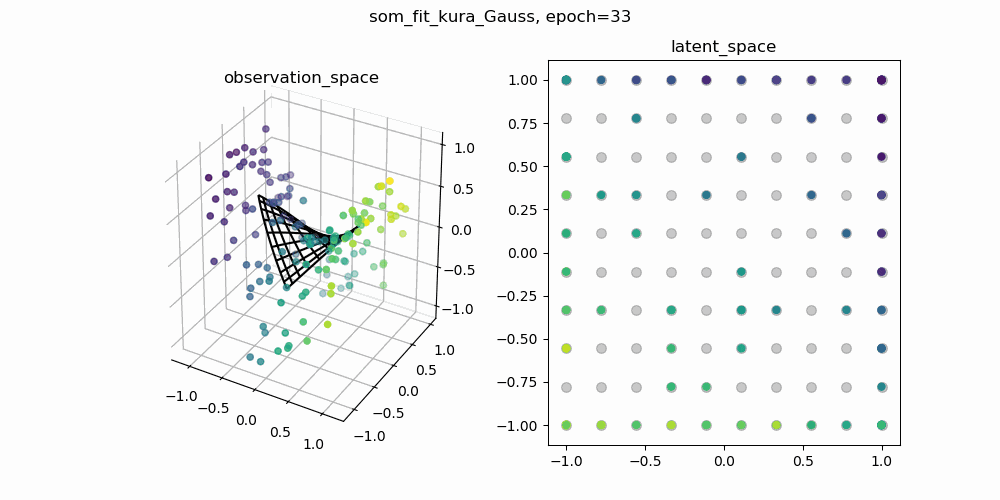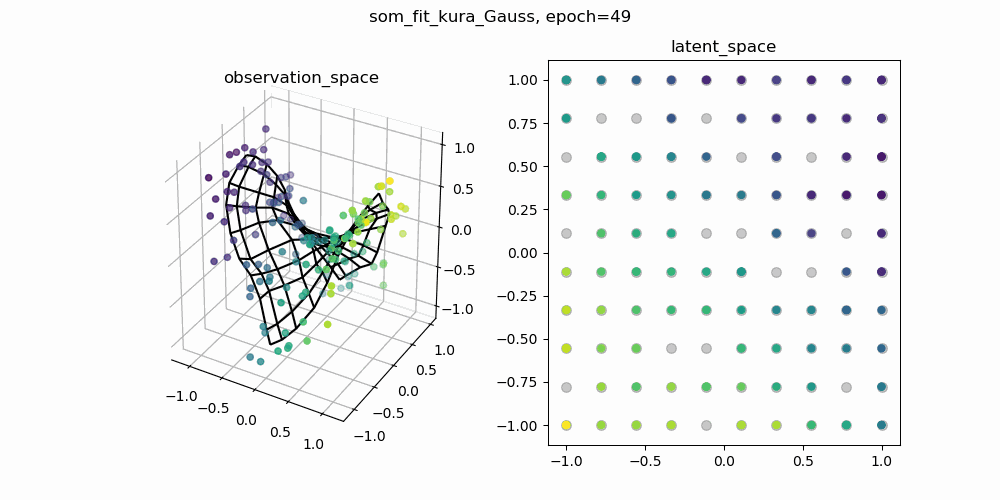
↑二乗距離で計算されたSOM
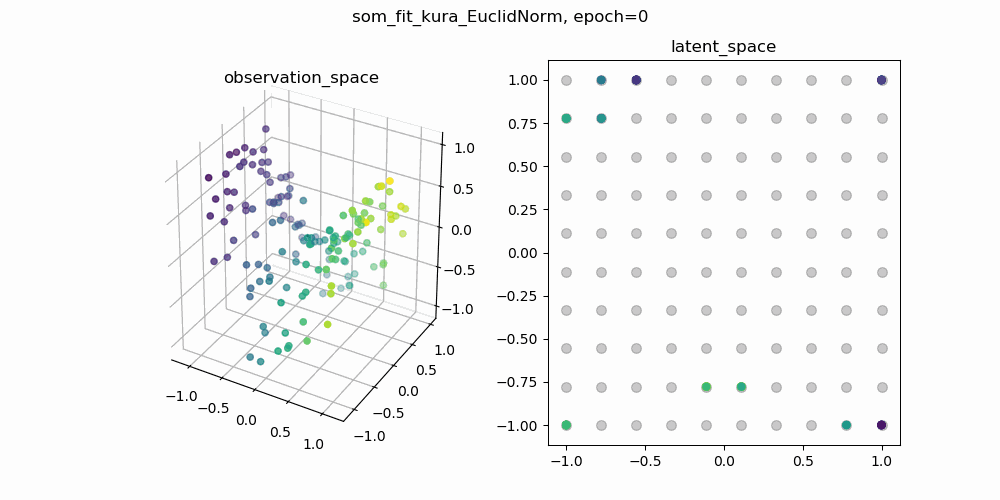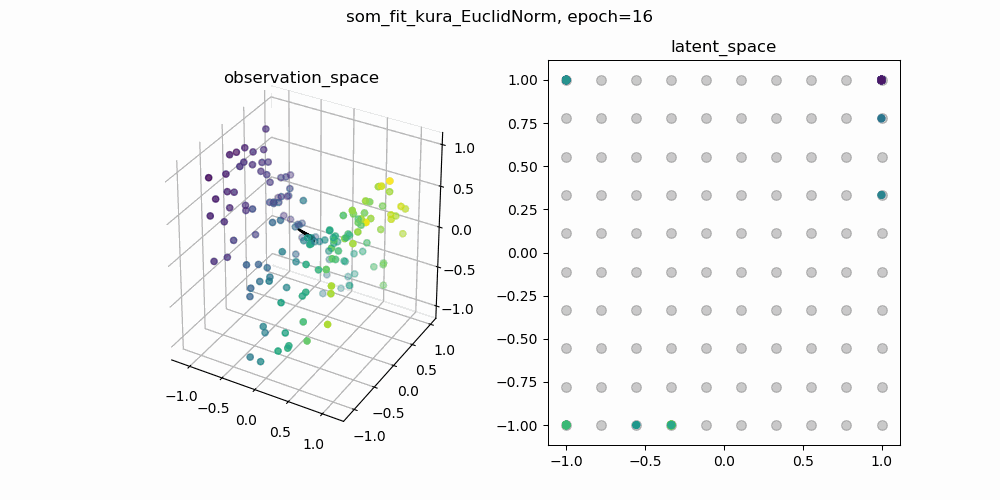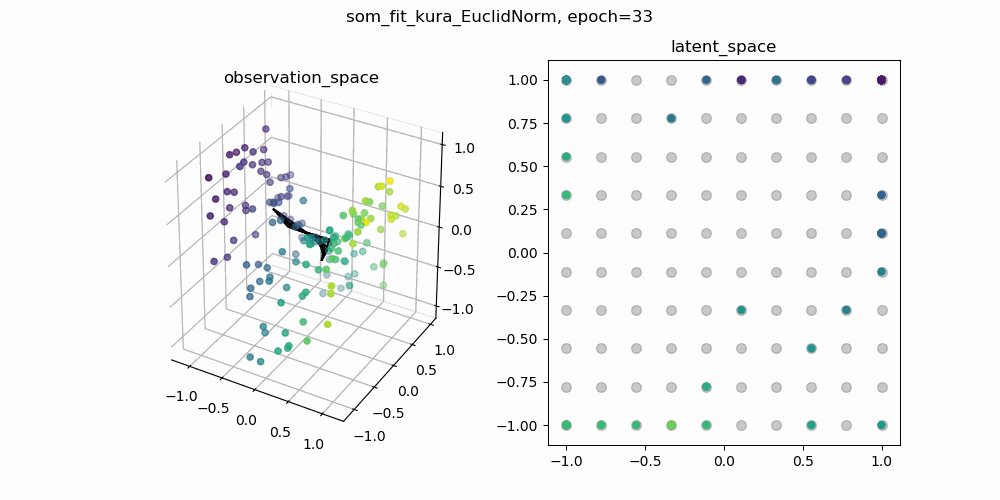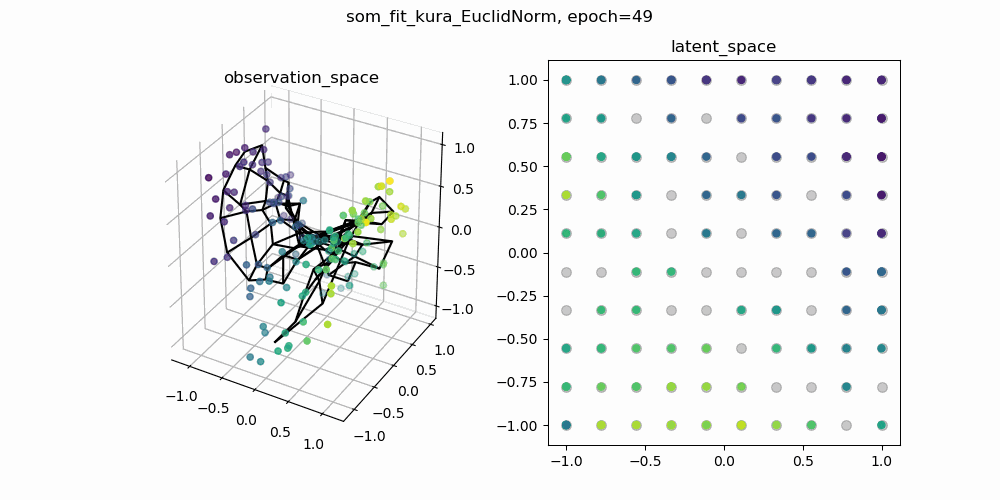↑ユークリッド距離で計算されたSOM
学習の初期値にも依るので一概には言えませんが，二乗距離で学習したSOMのほうが滑らかな多様体が得られているように見えます．ここから，「ユークリッド距離のほうが外れ値に敏感？overfittingしやすい？」などと予想をたてて，さらに深掘りすることができそうです．
「なんで二乗誤差で測るの？」への答え
ここまでいろいろと書いてきましたが，本題に入ります．
「なんで二乗誤差で測るの？」という問いに対する答えは，「計算が簡単だからとりあえず使っている」です．
とくに，目的関数を最適化しようとすると，一般には最小二乗法や勾配法を用いて最適化するのですが，その際に目的関数を微分する必要があるわけです．その微分計算が二乗誤差を用いる場合には簡単になります．
しかも，二乗距離を用いて誤差を測る場合，よっぽどおかしな挙動をしたり，極端に悪い結果になったりすることは中々起きないので，とりあえず試してみるには十分な性能を持っていると考えられるんですよね．
ただし，その誤差の測り方が最適である保証はないので，どこかのタイミングで誤差の測り方について再考した方が良いというわけですね．
おわりに
機械学習においては，二乗誤差と最小二乗法を組み合わせてやってみるという方法論はよくある話です．
適切な測り方と問題の解き方についてはよく考える必要があることが分かりました．
以上，ざっくりとですが，機械学習における二乗誤差の立ち位置についてまとめました．お役に立てれば幸いです．
参考文献
[1]イラストで学ぶ機械学習（講談社，2013）
[2]古川研究室のSOMドキュメント
[3]Variants of Unsupervised Kernel Regression: General Cost Functions (2007)
ミンコフスキー距離
[4]高校数学の美しい物語 - ノルムの意味とL1，L2，L∞ノルム
[5]このデータセットにはどの距離を用いればよいの？？～ユークリッド距離・マンハッタン距離・チェビシェフ距離・マハラノビス距離～