前回は、ブロックチェーン技術の土台に使われている数学の一つである、「有限体」について解説しました。
今回は、ブロックチェーン技術におけるもう一つの数学的な土台である「楕円曲線」について学んだことを解説していきます。
楕円曲線
楕円曲線は「楕円」ではない
まず「楕円曲線」という言葉だけを聞くと、楕円の形をした曲線のことかと思うかもしれません。
確かに楕円曲線の中には、楕円のような形の曲線が現れることもあります。(しかしこの場合の「楕円」は、数学的な意味での「楕円」ではありません)
しかし一般的に「楕円曲線」は楕円の形をしているわけではありません。
それではなぜ「楕円」という名前が入っているのかといえば、楕円曲線の点をパラメータ表示(共通の要素を使って$x$座標と$y$座標に分けて表示)するのに、「楕円積分」という数学上の概念を利用するからです。
「楕円積分」はもともと楕円の長さを求める際に必要とされるものでしたが、それ以外にも応用の幅が広くさまざまな場所で使われています!
興味のある方は調べてみてください!
楕円曲線の定義
上のような難しい説明だとなかなか理解ができないかもしれません。
しかし実際はそこまで難しいものではありません。
一般に、楕円曲線上の任意の点$(x,y)$は以下を満たします。
$$
y^2 = x^3 + ax+b
$$
ただし、$a$と$b$は任意の実数です。
楕円曲線を図示してみる
ここでは楕円曲線がどのような図形になるかを見ていきます。
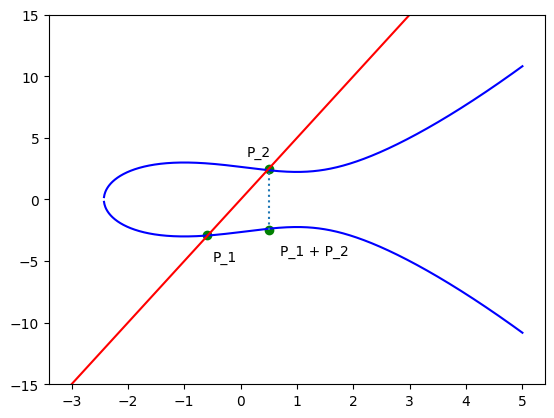
例えば、$a=0,b=7$の時には以下のようになります。
そしてこの$a=0,b=7$の時の楕円曲線はsecp256klと呼ばれるもので、ブロックチェーンを使った仮想通貨であるビットコインにおける暗号化で用いられています。
ちなみに以下がPythonのMatplotlibで描くソースです。
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 10, 1000)
y2 = (x**3 + 7)
y = np.sqrt(y2)
plt.plot(x, y, color='blue')
plt.plot(x, -y, color='blue')
#y2の平方根でプラマイゼロの部分が途切れてしまうので穴埋め
plt.scatter(-2,0, color='blue', s=1)
plt.show()
しかし実は私自身としてはこの描き方には納得がいっていません。
というのも、
#y2の平方根でプラマイゼロの部分が途切れてしまうので穴埋め
plt.scatter(-2,0, color='blue', s=1)
で実装している通り、$y^2$の根である$y$と$-y$の中間地点である$y=0$を別途穴埋めしているのです。
上記のプロットを見てみてください。
$(x,y)=(-2,0)$の点だけ少しコブのようになっていて、やや不自然なのがわかるでしょう。
しかし楕円曲線は、有理関数ではパラメータ表示ができないので、これより正確なプロットをしようと思えば、やはり楕円積分を使って$x$座標と$y$座標を表現して、それを実装する必要があるかと思います。
うーん、出来合いの何かパッケージとかないんですかね・・・。
プロットの作成方法で話が逸れてしまいましたが、$a$と$b$の値によって楕円曲線は大きく姿を変えます。
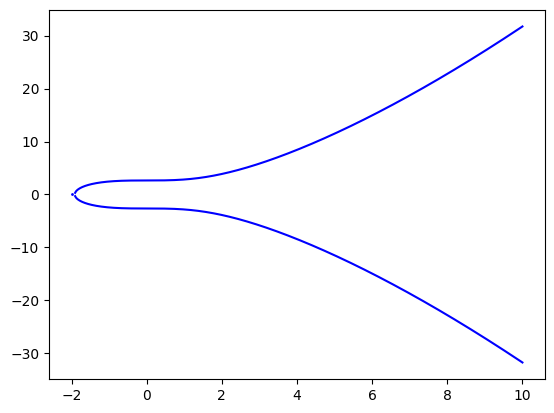
例えば、以下は$a=-5,b=8$の時です。

見ての通り、楕円曲線が二つの部分に分離してしまっています。
左側の方は、(数学的ではなく)普段使うような意味で「楕円」のような形をしていますね。
点の加法
さて、楕円曲線には「点の加法」と呼ばれる良い性質を持っています。
なぜそのようなことを行うのかといえば、それがブロックチェーン技術に役立つからです。
簡単に「点の加法」について説明すると、楕円曲線上の二つの点を選んだ時に、その二つの点を使って楕円曲線上の三つ目の点を作り出す操作のことです。
そしてこの二つの点から三つ目の点を作り出す操作が、普段我々が行なっている足し算(加法)と似た性質を持っているので、「点の加法」というネーミングになっています。
具体的に、「点の加法」の持つ性質は何かといえば、それは以下のようなものです。
- 単位元の存在
- 可換性がある
- 結合則を満たす
- 可逆性がある
といったことです。
ちょうど前回解説した「有限体」のところでも似たような話をしましたね。
これは「有限体」とは異なりますが、どちらも公理主義に基づく抽象数学なので似たもののように見えます。
さて、上記に挙げた性質を名前だけ聞いても何のことだか分からないと思いますので、ここで軽く説明しましょう!
まず単位元についてですが、これはある集合のとある性質をもつ要素のことです。
その性質とは、他の要素に単位元を加えても変化しないという性質です。
つまり、単位元を$0$と表記し、ある集合の中のある要素を$a$と書けば、
$$
a + 0 = a
$$
となるようなものです。
実数集合における「普通の」足し算のイメージを借りて、単位元を「ゼロ元」と呼ぶこともあります。
次に可換性についてです。
これは「加法」という操作の持つある性質のことです。
その性質とは、ある集合の二つの要素について、どちらに対して「加法」を行なっても結果は変わらないという性質です。
つまり、その集合の二つの要素をそれぞれ$a,b$と書けば、
$$
a + b = b + a
$$
となる操作の性質のことを可換といいます。
次に結合則についてです。
結合則とは、ある集合における三つの要素$a,b,c$について加法操作を行うときに、
$$
(a+b)+c=a+(b+c)
$$
を満たすような性質のことです。
単に前から順に足す必要はないよということですね。
最後に可逆性についてです。
こちらはある要素$a$に対して、
$$
a+b=0
$$
となるような$b$が存在するとき、$b$は$a$の逆元と呼びます。
足したら単位元になるものが存在するということですね。
さて、以上のように抽象的な性質を持つような、楕円曲線に対する操作とは具体的にどんなものでしょうか?
ある楕円曲線上の点$(x_1,y_1)$と$(x_2,y_2)$で考えてみましょう。
単に両者の成分を足すというのはどうでしょうか?
つまり、
$$
(x_1 + x_2,y_1+y_2)
$$
です。
この場合、上の四つの性質(単位元の存在、可換性の有無、結合則の有無、可逆性の有無)は全て満たしており、何だかこれで良さそうな気がします。
ですが、一般的に$(x_1 + x_2,y_1+y_2)$は楕円曲線上にありません。
実際、楕円曲線secp256klの$y^2=x^3+7$上の点$(1,8)$と$(-1,6)$について、
$$
(1,8)+(-1,6) =(0,14)
$$
ですが、$14^2\neq0^3+7$なのでsecp256kl上にはありません。
それでは、すべての条件を満たす「点の加法」について見ていきましょう!
楕円曲線上の点$P_1=(x_1, y_1)$と$P_2=(x_2,y_2)$について、$P_1+P_2$を得るための「点の加法」とは以下の操作です。
- $P_1$と$P_2$を通る直線とその楕円曲線の交点を、$x$軸に関して折り返した点を得る。
この操作は、
- 単位元の存在
- 可換性がある
- 結合則を満たす
- 可逆性がある
を満たしています。
2と3に関しては、実際に楕円曲線上に点を置いて上記の操作をすることですぐに確かめられますが、厄介なのは1と4です。
ここでポイントなのが、
垂直方向の無限の遠くにある点をこの操作における単位元としている
ということです。
例えば、上の図の$P_2$と$P_1+P_2$という二つの点は互いに逆元の関係であり、この2点を結んだ直線の無限の遠くに単位元があると考えます。
また、$P_1$とそこから垂直に無限に伸びた場所にある単位元を結ぶ線分と、楕円曲線の($P_1$ではない方の)交点が、$P_1$の逆元だということもわかります。
終わりに
今回はブロックチェーン技術で使われる数学のうち、楕円曲線について解説しました。
次は「有限体」と「楕円曲線」を使った暗号技術の基礎について解説しようと思います。