ガウス過程とはなにか

はじめに

研究でガウス過程回帰が必要になったので、『ガウス過程と機械学習』（講談社，著：持橋 大地，大羽 成征）で勉強を始めました。勉強開始時、ガウス過程が以下のように表現されているのは知っていました。

• 無限次元のガウス分布
• ランダムに関数 $f$ を出力する箱

ある程度理解できるとこの表現の通りだとわかるのですが、初読時にこれらを理論的に理解するのに苦戦しました。

これから勉強される方がこれらのとっつきから理論へスムーズに進めるよう、私なりの説明を残しておきます。本記事では、上の表現が以下のように補足されることを述べます。

• ガウス過程は、無限個の入力に対してガウス分布を与えるものである。（分布自体ではない）
• ガウス過程によって与えられた分布から、各入力に対する出力をサンプリングし、それらの対応をまとめたものが関数 $f$ であり、$f(x)=x^2$ のような具体的な関数形が得られるわけではない。

目次

1.ガウス過程とは
2.まとめ

1. ガウス過程とは

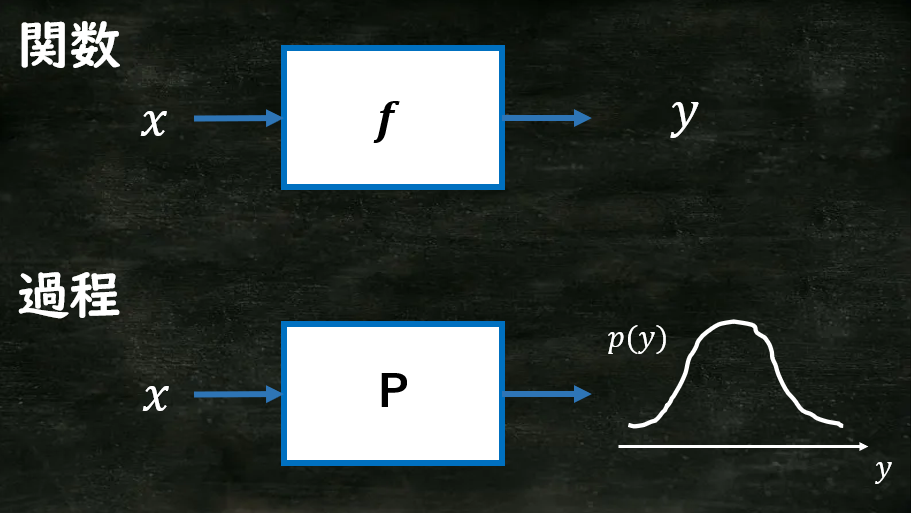
まずは「（確率）過程」¹という言葉を理解しましょう。

• （確率）過程：入力 $x$ に対して確率分布 $p(y)$ を与えるもの。
  

入力が入ったとき、関数が出力を確定的に返すのに対し、過程は出力についての確率分布を返します。この確率分布 $p(y)$ がガウス分布である過程を特にガウス過程といいます。入力 $x$ に対して具体的な出力 $y$ を得るには、この確率分布 $p(y)$ からサンプリングすればよいです。

では、ガウス過程が「ランダムに関数 $f$ を出す箱」と呼ばれる理由を説明します。
説明のために、ガウス過程のより厳密な定義を以下に載せます。

Def. ガウス過程
入力 $x_1, x_2, \ldots, x_N$（$N$は任意の自然数）に対応する出力のベクトル
$$\vec{f} = (f(x_1),f(x_2),\ldots,f(x_N))$$
が，平均を $\mu = (\mu(x_1),\mu(x_2),\ldots,\mu(x_N))$，共分散行列を $K$ $(K_{i,j}=k(x_i,x_j))$とする ²ガウス分布 $\mathcal{N}(\mu,K)$に従うとき，関数 $f$ はガウス過程に従うといい，
$$f \sim \mathcal{GP}(\mu(x),k(x_i,x_j))$$
と書く．

この定義で、$N$は任意の自然数なので $N \to \infty$ として、無限個の入力 $x_k$ $(k=1,2,\ldots)$ を考えてもよいです。無限個の入力を決定すると、平均 $\mu$ と共分散行列 $K$ が決まり、無限次元のガウス分布 $\mathcal{N}(\mu,K)$ ができます。そしてサンプリングによって、この分布から各入力 $x_k$ に対する出力 $y_k$ がそれぞれランダムに決まります。得られた入出力の組$$(x_1,y_1),(x_2,y_2),\ldots$$をプロットすると以下の図のようになります。（簡単のため入力は１次元としています。）

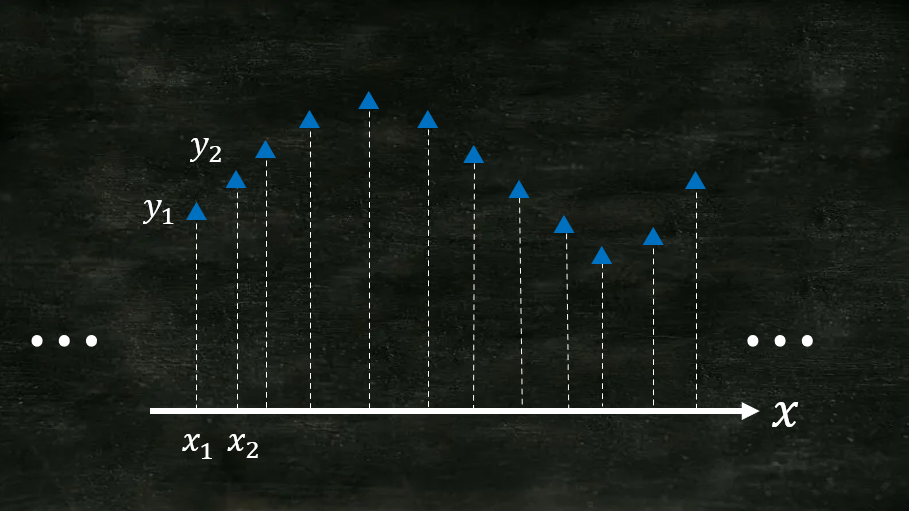
図を見ると、何かグラフが浮かび上がっているように見えます。これがガウス過程によって生成された関数（箱から出た関数）のグラフです。しかし、この関数は $f(x)=x^2$ のように具体的に書けるわけではありません。イメージとしては、$x$ と $y$ の大きな対応表が得られたような状態になります。

以上が、ガウス過程（箱）から関数が出る説明になりますが、ガウス過程を理解するポイントは以下の認識だと思います。

　「具体的な関数形（$f(x)=x^2$とか）ではなく、任意の入力 $x$ から出力 $y$ への対応が出てくる 」

「入出力の対応＝関数」は確かにそうなんですが、それが$f(x)=～$の形で統一的に書けると思い込むとわかりづらくなると思います。

2. まとめ

ガウス過程から関数が出てくる流れは以下のようになります。
（１）入力 $x$ を決定
（２）ガウス分布 $\mathcal{N}(\mu(x), k(x_i, x_j))$ を計算
（３）$\mathcal{N}(\mu(x),k(x_i, x_j))$ から入力 $x$ に対する出力 $y$ をサンプリング
（４）任意の入力 $x$ と出力　$y$ の対応（関数）が出る

ご意見・ご指摘がございましたら、コメントまでお願いします。

本記事をお読み頂き、ありがとうございました。

1. 元々、理論の対象が時系列データ（入力 $x$ が時刻 $t$ ）だったので「過程」という語が使われているようですが、「確率場」と置き換えるとわかりやすいように感じました。この換言は ガウス過程回帰の基礎（赤穂 昭太郎） に記載がありました。 ↩

2. $\mu(x)$は平均関数、$k(x_i,x_j)$はカーネル関数と呼ばれる関数です。 ↩