この記事は,StanとRでベイズ統計モデリングに関する読書会(Osaka.Stan#2)における補足資料です。
なお当日の読書会発表資料は,こちらで公開しています。
第四章(StanとRStanをはじめよう)以降は,データの特徴を可視化するために有益なggplot2コードが紹介されています。ggplot2はとても素晴らしいRパッケージなのですが,作図コードが長くなってしまう傾向があります。その長さゆえに敬遠されてしまってはもったいないと思い,極力短く書き換えたいと思った次第です。
具体的には,公開されているサンプルコードから,見栄え調整のための部分をごっそり省略し,最低限必要な部分だけを抜き出したり,dplyrパッケージを使って書き換えたりしました。一人でも多くの方に,ggplot2を愛用していただければ嬉しいです。
なお本記事では,第四章のみを対象にしています。
また,オリジナルのコードは転記しておりませんので,上記のサポートページをご参照ください。
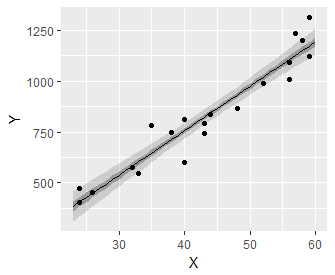
単回帰分析における信頼区間(fig4-3.Rファイル)
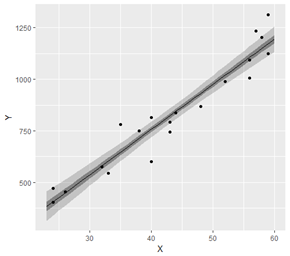
描きたいグラフは以下です。年齢Xで年収Yを直線回帰しています。薄い灰色の帯が95%信頼区間,濃い帯が50%信頼区間です。
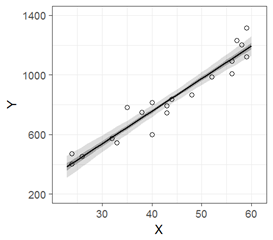
文字数を減らすことを最優先にすると,おそらく以下のような書き方になると思います。
library(ggplot2)
d <- read.csv(file='input/data-salary.txt')
res_lm <- lm(Y ~ X, data=d)
X_new <- data.frame(X=23:60)
conf_95 <- cbind(X_new, predict(res_lm, X_new, interval='confidence', level=0.95))
conf_50 <- cbind(X_new, predict(res_lm, X_new, interval='confidence', level=0.50))
p <- ggplot(data=conf_95, aes(x=X))
p <- p + geom_ribbon(aes(ymin=lwr, ymax=upr), alpha=1/6)
p <- p + geom_ribbon(data=conf_50, aes(ymin=lwr, ymax=upr), alpha=2/6)
p <- p + geom_line(aes(y=fit))
p <- p + geom_point(data=d, aes(y=Y))
p <- p + labs(y='Y')
ggsave(p, file='output/fig4-3-left.png', dpi=300, w=4, h=3)
少し記述量を減らしても同じような作図が出来ました。
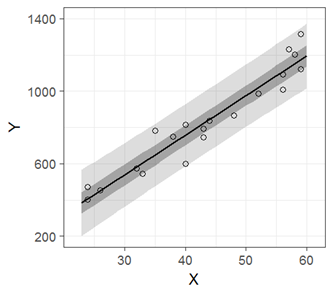
単回帰分析における予測区間(fig4-3.Rファイル)
同じく文字数を減らすことを最優先にすると,以下のような書き方になると思います。
library(ggplot2)
d <- read.csv(file='input/data-salary.txt')
res_lm <- lm(Y ~ X, data=d)
X_new <- data.frame(X=23:60)
pred_95 <- cbind(X_new, predict(res_lm, X_new, interval='prediction', level=0.95))
pred_50 <- cbind(X_new, predict(res_lm, X_new, interval='prediction', level=0.50))
p <- ggplot(data=pred_95, aes(x=X))
p <- p + geom_ribbon(aes(ymin=lwr, ymax=upr), alpha=1/6)
p <- p + geom_ribbon(data=pred_50, aes(ymin=lwr, ymax=upr), alpha=2/6)
p <- p + geom_line(aes(y=fit))
p <- p + geom_point(data=d, aes(y=Y))
p <- p + labs(y='Y')
ggsave(p, file='output/fig4-3-right.png', dpi=300, w=4, h=3)
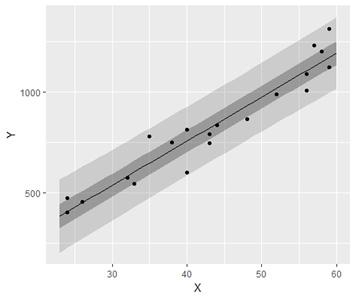
単回帰分析におけるベイズ信頼区間(fig4-8.Rファイル)
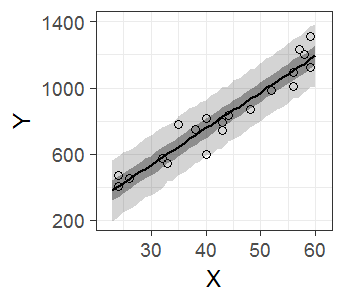
薄い灰色の帯が95%ベイズ信頼区間,濃い帯が50%ベイズ信頼区間です。
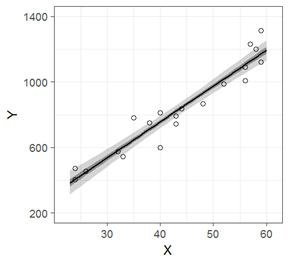
本書では,読者のR環境によらず作図が出来るように,あえてggplot2以外のパッケージは使わずにコードを書いていると思います。
ただ,この図に関しては,(1)オリジナルのコードがかなり長いこと,(2)apply系が使われていて,不慣れな人(本記事の執筆者を含む)には挙動が分かりづらいかもしれないこと,(3)行列の転置関数t()が使われていて,イメージしづらいかもしれないこと,という理由から,dplyrパッケージを使って書き換えることにしました。
また,最低限必要なggplot2コードのみを記載しました。
library(dplyr)
library(ggplot2)
load('output/result-model4-5.RData')
ms <- rstan::extract(fit)
temp <- NULL
for(i in 23:60){
temp2 <- data.frame(age=i, cred=(ms$a + ms$b * i))
temp <- rbind(temp, temp2)
}
temp <- temp %>%
dplyr::group_by(age) %>%
dplyr::summarise(p2.5=quantile(cred, probs=0.025),
p25=quantile(cred, probs=0.25),
p50=quantile(cred, probs=0.50),
p75=quantile(cred, probs=0.75),
p97.5=quantile(cred, probs=0.975))
p <- ggplot(data=temp, aes(x=age))
p <- p + geom_ribbon(aes(ymin=p2.5, ymax=p97.5), fill='black', alpha=1/6)
p <- p + geom_ribbon(aes(ymin=p25, ymax=p75), fill='black', alpha=2/6)
p <- p + geom_line(aes(y=p50))
p <- p + geom_point(data=d, aes(x=X, y=Y))
p <- p + labs(y="Y", x="X")
ggsave(file='output/fig4-8-left.png', plot=p, dpi=300, w=4, h=3)
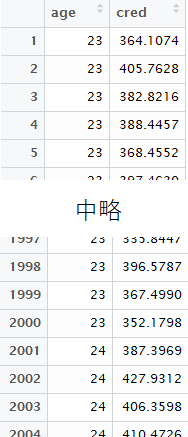
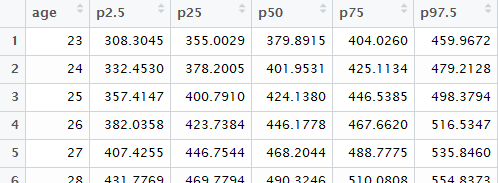
forループのところは,これはこれで分かりにくいかもしれません...。ここでは,以下のように年齢ごとの予測値の分布を縦方向に延々と並べる作業をしています。
そのあとdplyrパッケージのgroup_by()とsummarise()を併用して,年齢ごとに各パーセンタイルでの値を求めています。
ここまできたら,あとはggplot2で作図するだけです。
単回帰分析におけるベイズ予測区間(fig4-8.Rファイル)
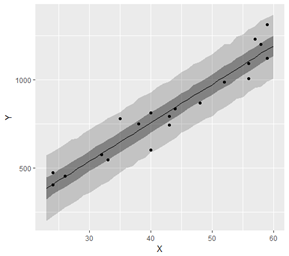
薄い灰色の帯が95%ベイズ予測区間,濃い帯が50%ベイズ予測区間です。
ベイズ信頼区間の場合とほとんど同じ書き換え方をしています。
library(dplyr)
library(ggplot2)
load('output/result-model4-5.RData')
ms <- rstan::extract(fit)
temp <- NULL
for(i in 23:60){
temp2 <- data.frame(age=i,
pred=rnorm(n=length(ms$lp__),mean=(ms$a + ms$b * i), sd=ms$sigma))
temp <- rbind(temp, temp2)
}
temp <- temp %>%
dplyr::group_by(age) %>%
dplyr::summarise(p2.5=quantile(pred, probs=0.025),
p25=quantile(pred, probs=0.25),
p50=quantile(pred, probs=0.50),
p75=quantile(pred, probs=0.75),
p97.5=quantile(pred, probs=0.975))
p <- ggplot(data=temp, aes(x=age))
p <- p + geom_ribbon(aes(ymin=p2.5, ymax=p97.5), fill='black', alpha=1/6)
p <- p + geom_ribbon(aes(ymin=p25, ymax=p75), fill='black', alpha=2/6)
p <- p + geom_line(aes(y=p50))
p <- p + geom_point(data=d, aes(x=X, y=Y))
p <- p + labs(y="Y", x="X")
ggsave(file='output/fig4-8-right.png', plot=p, dpi=300, w=4, h=3)
やはり同じような図が描けました。
おわりに
今回はggplot2を初めて触る方を想定し,とにかく作図コードの長さから受ける”圧”みたいなものを減らすために,見栄え調整のための部分をごっそり省略しました。ただ,そうは言っても,結果を他者と共有する場合などにおいては,見栄えは大事です。徐々に見栄え調整のためのコードも追記していき,ggplot2を楽しんでいただけたら幸いです。