はじめに
こんにちは。AtCoder青色のkym3535と申します。先日のABC247 F問題「Cards」が、複数の競プロ典型を組み合わせて解くすばらしい融合問題で、解いていて内心感動してしまいました。そこで使われる着眼点や典型解法をぜひ紹介したく、解説記事を書いてみたいと思います。
問題
(AtCoder Beginner Contest 247) F - Cards
$1,...,N$の番号がついた$N$枚のカードがあり、カード$i$の表には$P_i$が、裏には$Q_i$が書かれています。
ここで、$P=(P_1,...,P_N)$および$Q=(Q_1,...,Q_N)$はそれぞれ$(1,2,...,N)$の並び替えです。
$N$枚のカードから何枚かを選ぶ方法のうち、次の条件を満たすものは何通りありますか?$998244353$で割った余りを求めてください。
条件:$1,2,...,N$のどの数も選んだカードのいずれかに書かれている
制約
- $1\le N\le 2\times 10^5$
- $1\le P_i,Q_i\le N$
- $P,Q$はそれぞれ$(1,2,...,N)$の並び替えである
- 入力に含まれる値はすべて整数である。
考察
問題の理解
まずは問題設定を理解するところから始めましょう。問題文の入力例2を例に説明します。
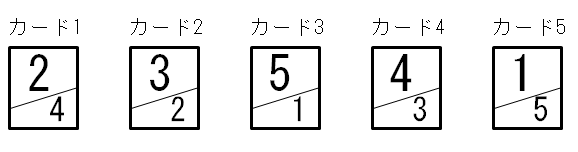
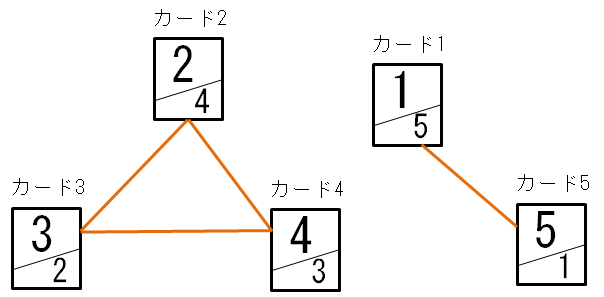
表と裏に数字が書かれたカードが5枚あります。下の図では、カードの表と裏に書かれた数字を、それぞれ斜線で区切って示してあります。
たとえば、カード1,3,4を選ぶ選び方は条件を満たしています。なぜなら、「1」はカード3に、「2」はカード1に、「3」はカード4に、「4」はカード1とカード4に、「5」はカード3に書かれているためです。
しかし、たとえばカード3,4,5を選ぶ選び方は条件を満たしていません。なぜなら、どのカードにも「2」が書かれていないためです。
なお、カードを選ぶ枚数に上限や下限はありません。当然、すべてのカードを選ぶ選び方は条件を満たしますし、カードを0枚選ぶ(一つも選ばない)選び方は条件を満たしません。
問題の言い換え
選んだカードに書かれている数字がすべての数字を網羅できているかを考えるのはすこし骨が折れます。そこで、発想を逆転させて、「使用しないカードを選ぶ」組み合わせを考えることにしてみます。競プロでの典型的なアプローチである、「問題を言い換える」ですね。
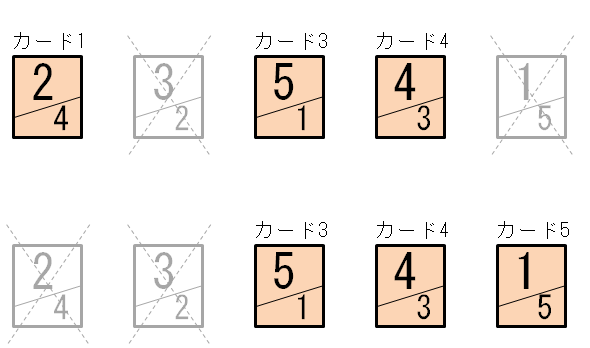
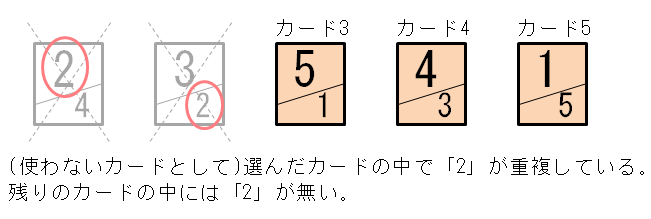
では、どのような選び方なら、条件を満たすでしょうか?実は、「(使わないカードとして)選んだカードの中に、重複する数字がないなら、残りのカードは条件を満たす」ことがいえます。
逆に、「(使わないカードとして)選んだカードの中に、重複する数字があるなら、残りのカードにはその数字が書かれていないので、条件を満たさない」こともいえます。
しかし、これだけではまだ簡単には組み合わせの数を数え上げられません。もう一段考察を進める必要があります。
グラフの問題への帰着
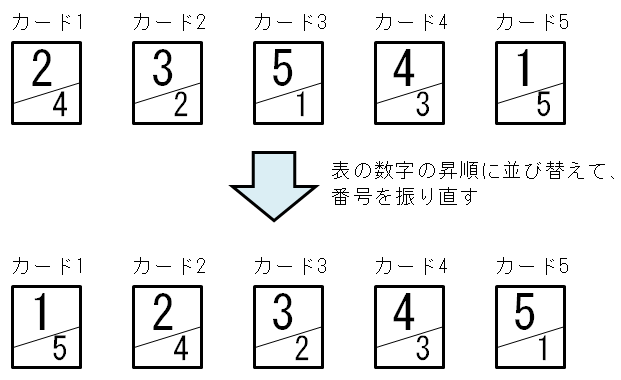
もう少し考察を進める前に、カードをわかりやすく並べ替えます。問題の性質上、カードの並び順は組み合わせの数には影響しません。そこで、表に書かれている数字が昇順になるように並び替えたうえで、改めてカード$1,2,...,N$の番号を振り直すことにします。
そうすると、カード$1$の表には数字の「1」が、カード$2$の表には数字の「2」が、...、カード$i$の表には数字の「$i$」が書かれていることになります。。
さて、前の節での考察より、使わないカードとして選んだカードの中に重複する数字があると、残りのカードは条件を満たさないことがわかりました。この、一緒に選んではいけないカードの組み合わせを図示してみましょう。
たとえば、カード$1$は表に「1」、裏に「5」が書いてあるので、カード$1$と$5$を一緒に選ぶと、数字の「5」が重複することになります。
カード$2$は表に「2」、裏に「4」なので、カード$2$と$4$を一緒に選ぶと数字の「4」が重複してしまいます。
このように、一緒に選んではいけないカード同士を線で結ぶと、次の図のようになります。
カードを頂点、一緒に選んではいけない組み合わせを辺とするグラフ構造が見えてきました。
元々の問いは、「条件を満たすカードの選び方は全部で何通りか」でした。しかし、このグラフを用いて考えると、問いは次のように言い換えられます。
「このグラフから0個以上の頂点を選ぶ方法のうち、隣り合った頂点を選ばない方法は全部で何通りか」
グラフの形についての考察
このグラフの重要な性質として、形が
- $N$角形$(N\ge 3)$
- 2頂点を辺で結んだ形
- 1頂点
のいずれかになることが挙げられます。
たとえばカード2なら、その裏には数字の「4」が書かれているため、カード2と4を一緒に選んではいけない、裏に「2」が書かれているカードはカード3なので、カード2と3を一緒に選んではいけない、というように、表と裏で合計2頂点と結ばれる事になります。このような関係がすべての頂点について成り立つため、グラフは$N$角形のような形になります。なお、このような形のグラフのことを「サイクル」と言うそうです。
ただし、カード1とカード5のように、互いに自分のカードの裏に相手のカードの表の数字が書いてあるような関係だった場合は、この2つの頂点を辺で結んだ形になります。
また、仮に表と裏に書かれている数字が同じカードがあったなら、そのカードはほかのどのカードとも辺で結ばれないことになります。このようなカードは、(使わないカードとして)選ぶ事が出来ません。
連結成分ごとの問題への帰着
この図の例では、グラフは2つの連結成分に分かれています。そして、問題の性質上、異なる連結成分同士は、「隣り合った頂点を選ばない」という条件に影響を与えません。
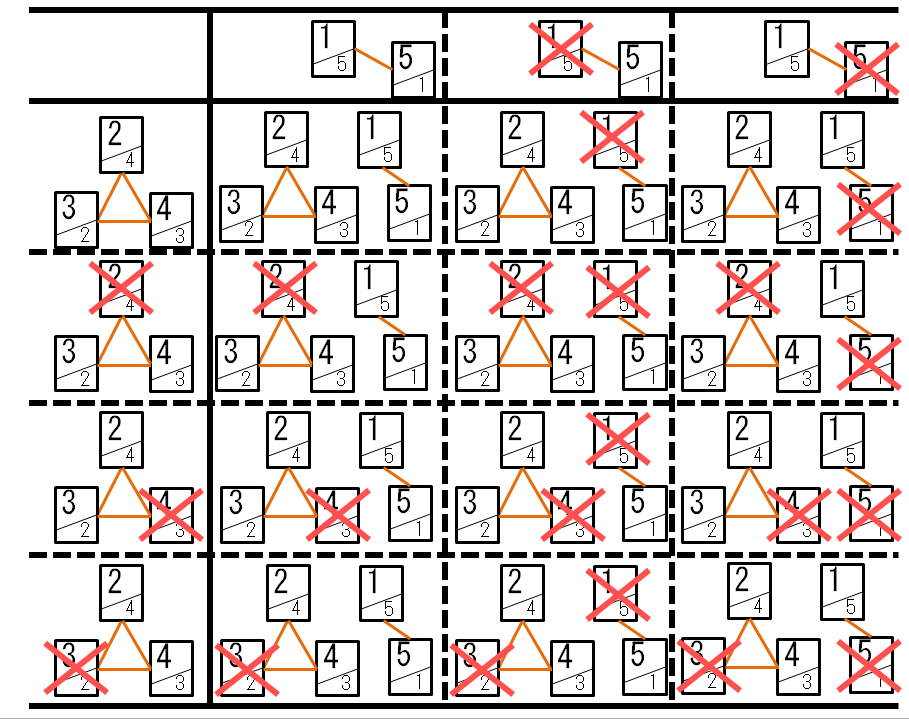
ということは、連結成分ごとに「隣り合った頂点を選ばない」選び方が何通りかを求めて、それを掛け合わせると、全体での組み合わせの数になります。この例でいうと、以下のようなイメージです。
この図では、選んだ頂点に赤で×印を打って示しています。3頂点の三角形から0個以上の頂点を選ぶ方法のうち、隣り合った頂点を選ばない方法は4通りあります。また、2頂点を結んだグラフから0個以上の頂点を選ぶ方法のうち、隣り合った頂点を選ばない方法は3通りあります。したがって、全体では$4\times 3=12$(通り)の選び方があります。
これにより、全体の問題は、N頂点サイクルについての問題に帰着することが出来ました。
N頂点サイクルの問題の解をDPで求める
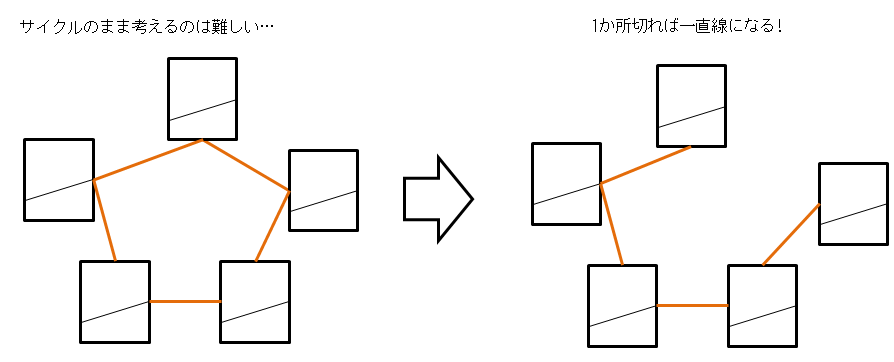
N頂点サイクルについての問題に帰着することが出来ました。しかし、少し考えてみても、組み合わせの数を式一本で表して求めるのは難しそうです。
そこで、これも典型的なアプローチかもしれないですが、サイクルで考えるのではなく、サイクルの1か所を切った一直線のグラフの問題で考えてみます。
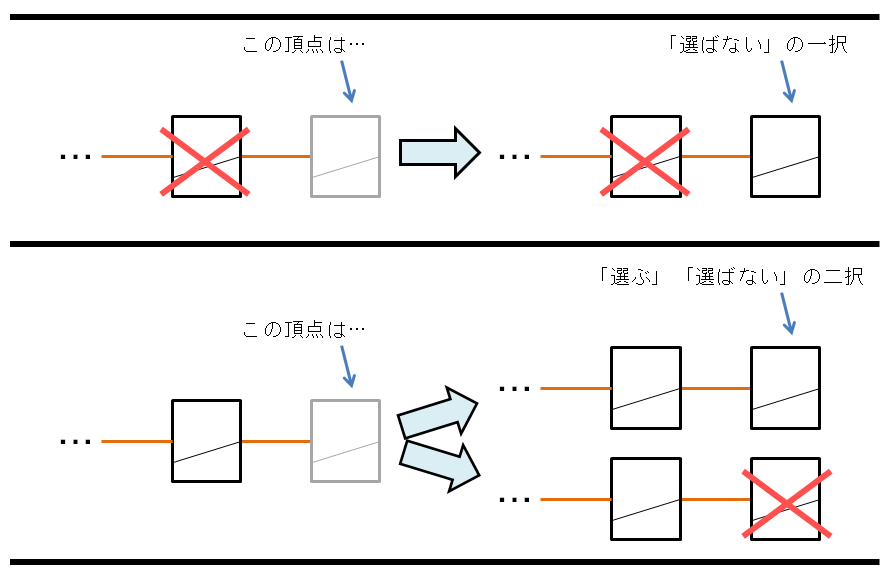
左の頂点から順に、選ぶか選ばないかを決めていくことにすると、ある一つの頂点を選んだ場合、その一つ右の頂点は「選ばない」の一択しかありません。なぜなら、隣り合った頂点を選んではいけないからです。逆に、ある一つの頂点を選ばなかった場合、その一つ右の頂点は「選ぶ」「選ばない」の二択があります。
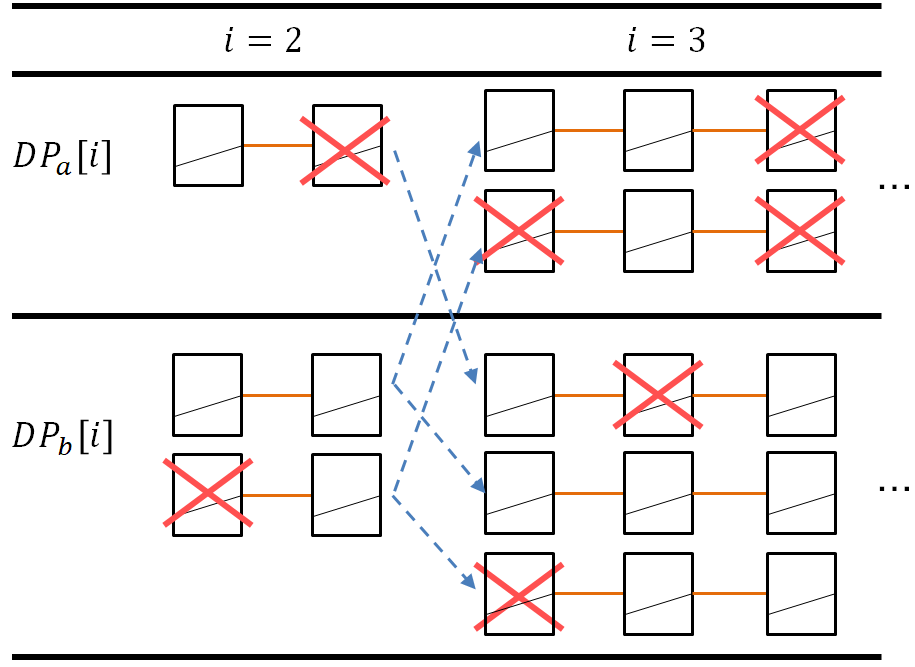
この関係に気づくと、すべての組み合わせの数はDPで求められそうだと分かります。$i$頂点の一直線のグラフから、頂点をいくつか選ぶ組み合わせのうち、$i$番目の頂点を選んでいるものの数を$DP_{a}[i]$(通り)、$i$番目の頂点を選んでいないものの数を$DP_{b}[i]$(通り)とすると、次のような関係が成り立ちます。
- $DP_{a}[i+1] = DP_{b}[i]$
- $DP_{b}[i+1] = DP_{a}[i] + DP_{b}[i]$
- $DP_{a}[1] = 1$
- $DP_{b}[1] = 1$
$i=2$から$3$へ遷移するときの脳内イメージを、以下の図に示します。
サイクルの場合の解き方
ところで、問題で問われているのは$N$頂点サイクルの場合でした。一直線の場合の問題を解いた結果を、そのままサイクルの場合についても適用できるでしょうか。
一直線のグラフをサイクルに戻すには、先頭と末尾の要素を辺でつなぐことになります。そのため、先頭と末尾の両方を選ぶような組み合わせは、数に入れてはいけません。この対策をするには、先ほどのDPをさらに二つに分けて、
- $DP_{aa}[i]$ : 先頭と$i$番目の頂点を両方選んでいるものの数
- $DP_{ab}[i]$ : 先頭は選び、$i$番目の頂点を選んでいないものの数
- $DP_{ba}[i]$ : 先頭は選ばず、$i$番目の頂点を選んでいるものの数
- $DP_{bb}[i]$ : 先頭と$i$番目の頂点を両方選んでいないものの数
の4つの変数を更新するDPを解けば良いことになります。DPの遷移は以下の通りです。
- $DP_{aa}[i+1] = DP_{ab}[i]$
- $DP_{ab}[i+1] = DP_{aa}[i] + DP_{ab}[i]$
- $DP_{ba}[i+1] = DP_{bb}[i]$
- $DP_{bb}[i+1] = DP_{ba}[i] + DP_{bb}[i]$
- $DP_{aa}[1] = 1$
- $DP_{ab}[1] = 0$
- $DP_{ba}[1] = 0$
- $DP_{bb}[1] = 1$
こうして$DP[N]$まで計算したら、求める組み合わせは$DP_{ab}[N]+DP_{ba}[N]+DP_{bb}[N]$となります。ここで、$N=1,2$の場合についても確認すると、この計算式で正しく答えが求まるので、例外処理は不要です。
このDPの計算は、プログラム全体で最初に1回だけ走らせておけば、あとは結果を流用できます。DPを$O(N)$で前計算しておいて、あとで$O(1)$でその結果を使用するのも、競プロの典型パターンですね。
実装
考察はかなり長かったですが、実装はそこまで複雑ではありません。サイクルの連結成分を求める、比較的単純なDPを前計算する、組み合わせをかけ算で求める、と、分量こそ多いですが、一つ一つのタスクは軽めです。
コンテスト後に清書したコードは以下の通りです。
清書した解答【提出 #30983739】
import sys
def input():
return sys.stdin.readline()[:-1]
P= 998244353
n = int(input())
p = list(map(int, input().split()))
q = list(map(int, input().split()))
nodes = list(range(1,n+1))
pq = [(pi,qi) for pi,qi in zip(p,q)]
# piの昇順でソートすると、後でサイクルの長さを計算するときに楽。
pq.sort()
# サイクルの長さのリストを作る。
cycle_len_list = []
visited = [False]*n
# 深さ優先探索で、自分のところに返ってくるまでたどり続ける。
for i in range(n):
if visited[i]:
continue
j = i
cycle_len = 0
while not visited[j]:
visited[j] = True
j = pq[j][1] -1
cycle_len += 1
cycle_len_list.append(cycle_len)
max_n = max(cycle_len_list)
# DPを前計算する。i頂点一直線のグラフで、互いに隣接しないよう0個以上の頂点を選ぶ組み合わせのうち、
# DP_aa[i] : 左端と右端の頂点を両方選ぶ組み合わせの数
# DP_ab[i] : 左端は選ぶが右端は選ばない組み合わせの数
# DP_ba[i] : 左端は選ばないが右端は選ぶ組み合わせの数
# DP_bb[i] : 左端と右端の頂点を両方選ばない組み合わせの数
dp_aa =[0]*(max_n+1)
dp_ab =[0]*(max_n+1)
dp_ba =[0]*(max_n+1)
dp_bb =[0]*(max_n+1)
dp_aa[1] = 1
dp_bb[1] = 1
for i in range(2,max_n+1):
dp_aa[i] = dp_ab[i-1]
dp_ab[i] = (dp_ab[i-1] + dp_aa[i-1])%P
dp_ba[i] = dp_bb[i-1]
dp_bb[i] = (dp_bb[i-1] + dp_ba[i-1])%P
# すべての組み合わせの数を求める
ans = 1
for s in cycle_len_list:
# s頂点サイクルで、互いに隣接しないよう0個以上の頂点を選ぶ組み合わせの数
ansi = (dp_ab[s] + dp_ba[s] + dp_bb[s])%P
ans = (ans * ansi )%P
print(ans)
感想
この問題はDPとグラフの融合問題となっており、非常に解きごたえがありました。考察の過程では多くの典型テクニックを使用し、解いていて自分自身の成長を感じることが出来ました。私自身、ABCやARCには何度も参加してきましたが、ここ半年の中でも1位・2位を争う良問だと感じます。
必要なアルゴリズムそのもは、そこまで難しいものではないので、緑や水色の方々でもこの解説を参考にACできる可能性は高いと思います。ぜひ挑戦をおすすめします。この1問だけで、さまざまな考察典型テクニックに触れることが出来ますよ。
その他
この回のABCのA~F問題について、@u2dayoさんが解説記事を投稿されています。こちらも参考にどうぞ。