AtCoder青色のkym3535と申します。昨日のARC137ではA・Bの2完後、C問題は方針が見えず、D問題もいいところまで考察が進んだものの実装できず、少し残念な結果となってしまいました。
しかし、その後D問題の考察を進めた結果、うまく解くことが出来ましたので、解説記事を書いてみたいと思います。
※本記事の図は、手書きでノートに書いたものを写真撮影して取り込んでいるため、非常に汚くなっております。どうかご容赦ください。
問題
(AtCoder Regular Contest 137) D - Prefix XORs
長さ$N$の正数列 $a=(a_1,a_2,\cdots,a_N)$ および整数$M$が与えられます。
各 $k=1,2,\dots,M$ について、以下の操作をちょうど $k$ 回行った後の $a_N$ の値を求めてください。
・すべての$i(1 \leq i \leq N)$について、 $a_i$の値を$a_1 \oplus a_2 \oplus \cdots \oplus a_i$で置き換える。この置き換えはすべての$i$に対して同時に行う。
※解説の都合上、数列の文字を小文字の$a$としました。
考察
規則性をつかむ
まずは問題文にある入力例のケースを手元で確認してみて、規則性を考えてみます。
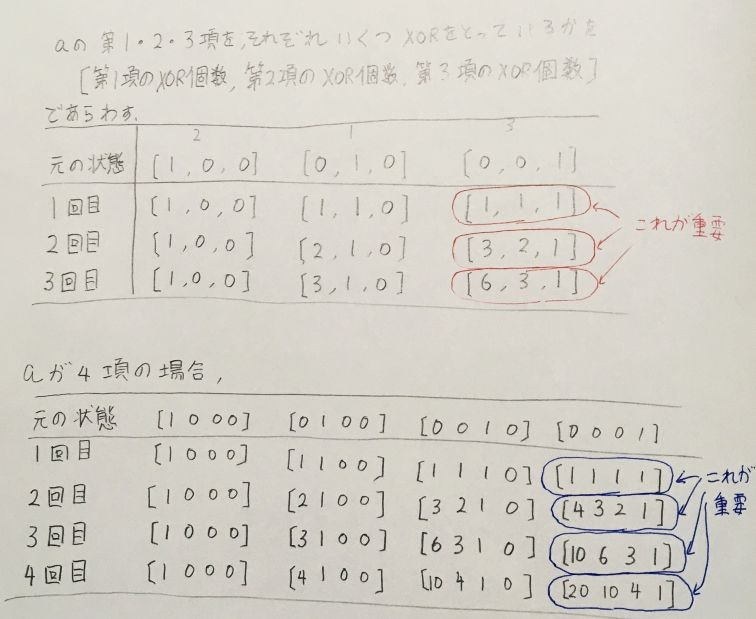
ここで一工夫ですが、$\oplus$(XOR)を計算するのは後回しにしておいて、どの数が何回、各項の計算に現れるかを観察してみます。
上の図に示したとおり、操作を重ねるごとに各項に含まれる$\oplus$の個数が増えていきます。
この問題で重要なのは、最終項の1回目・2回目の値に、$a_1,a_2,a_3$の値がそれぞれいくつ含まれているかということです。また、同じ数字を2回XORすると消えて無くなる性質があるため、最終的には$a_1,a_2,a_3$の値が含まれている個数の偶奇が重要になります。
ただ、ここでは偶奇に注目するのはいったん保留しておいて、そのまま数を数えることにします。$a_n$が3項の場合、4項の場合それぞれで、$k$回目の操作の後の最終項に含まれる$a_n$の個数を計算してみると、以下の図のようになります。
この図に示したとおり、$1, 2, 3, 4, 6, 10, \cdots $ といった数の並びが登場します。これらの数を見てピンとひらめくのが、パスカルの三角形です。実際にパスカルの三角形を書いて眺めてみると、上図で赤丸・青丸で囲った部分が、パスカルの三角形にも登場していることがわかります。
パスカルの三角形の偶奇に関する考察
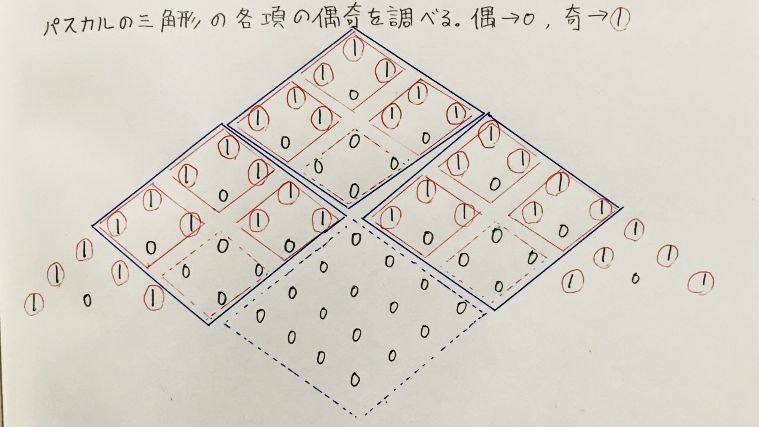
さて、重要なのは各項の個数の偶奇でした。そして、各項の個数はパスカルの三角形に現れることがわかりました。では、パスカルの三角形の各数字の偶奇を書き出してみましょう。下図では見やすさのため、「1」となった部分を赤丸で囲っています。
綺麗な三角形模様があらわれました。小さな三角形が3つ集まって中くらいの三角形を作り、その中くらいの三角形が3つ集まって大きな三角形を作り、…と無限に続くフラクタル模様が見えます。これは「シェルピンスキーのギャスケット - Wikipedia」に他なりません。
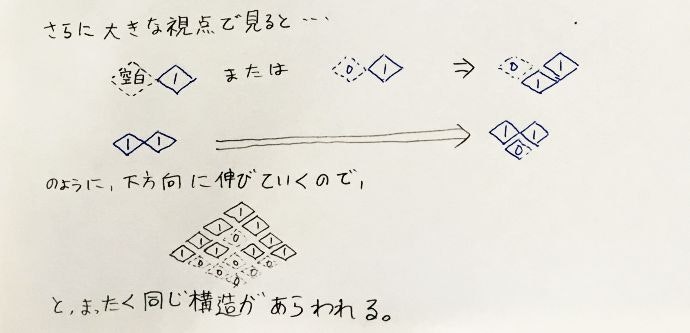
フラクタル構造ということは、大きな形の中に小さな形が含まれる、という構造があるはずです。注目したい数列がナナメ方向に並ぶことも踏まえて、この数の並びをじっと見ると、下の図のような正方形の数の並びの再帰構造が見えてきます。
この図で実線で囲んだ部分が「ON」、点線で囲んだ部分が「OFF」に相当するものと考えると、一番小さな「1」「0」の数のところから含めて、綺麗な再帰構造になっています。
また、上図では4x4の大きさまでしか書いていませんが、8x8、16x16の大きさの正方形の並びについても、同様の構造が成り立っています。
FFTの考え方を応用
「要素数$N$の変換を表す行列の中に、要素数$N/2$の変換を表す行列が登場する」というのは、FFTで出てきたパターンです。今回もそれに似たパターンが見え隠れしますが、そのまま単純に行列計算の式で書き表すことはできません。なので、具体的な値で考えてみましょう。
FFTでは、要素数は2のべき乗としていました。また、入力の要素数と出力の要素数は常に等しくなっていました。これにならって、数列の要素数は2のべき乗、 $M$ は数列の要素数と等しい、と仮定します。(あとでこの仮定が成り立たない場合について考えます。)
また、どの項のXORをとっているかをわかりやすくするため、$a = (1000,0100,0010,0001)$(2進数表記)とします。また、この問題の答えを$A_i$と書くことにします。
FFTでは、要素数$N/2$の問題の答えを用いて、要素数$N$の問題の答えを高速に計算しています。それにならって、「$a$の前半2項の問題の答え」と「$a$の後半2項の問題の答え」がわかったと仮定すると、どうすれば$A_i$を効率的に計算できるか?を考えていきます。
上のノートの画像の通り、FFTで見たことのある演算構造が出てきました。バタフライ演算です。本家のバタフライ演算では全体にある数を掛けて足し算していましたが、今回のケースではXORをとっています。
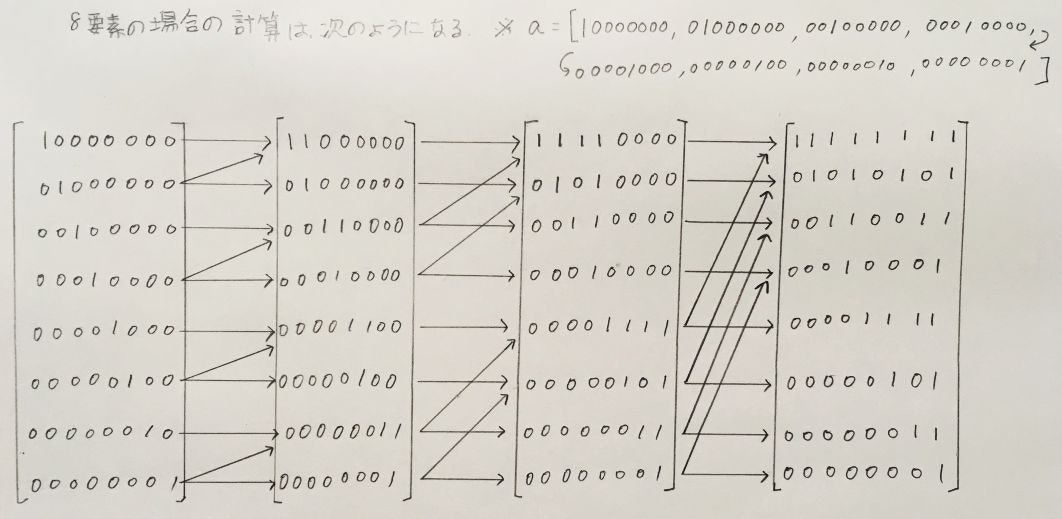
要素数8の場合の演算過程を図にすると、下図の通りとなります。非常に綺麗で規則的な構造が見えます。
要素数が2のべき乗でない場合
要素数が2のべき乗でない場合は、$a_n$の左側に$0$を適切な個数埋めて要素数を2のべき乗にすれば問題ありません。たとえば、$a_n=(3,1,4)$の場合、左に$0$を1個足して、$a_n=(0,3,1,4)$とすれば問題なく解けます。
Mが要素数より小さい場合
この場合は、操作を要素数に等しい回数実施して、その結果のうち先頭$M$項を出力すれば問題ありません。
Mが要素数より大きい場合
この場合は、$a_n$の要素数が$M$より大きな2のべき乗になるように$0$で埋めてから計算すれば問題なく解けます。
たとえば$a_n=(1,2,4)$、$M=7$の場合は、$a_n$の要素数が8になるようにゼロ埋めして、
$a_n=(0,0,0,0,0,1,2,4)$
として、8回操作を行った結果を計算します。その結果は
$A_n=(7,5,6,4,7,5,6,4)$
となるので、求めるべき答えは
$A_n=(7,5,6,4,7,5,6)$
となります。
実装
要素数8の演算過程の図のように、数列の塊ごとに計算するような場面では、numpy.ndarrayを用いると高速に処理できます。
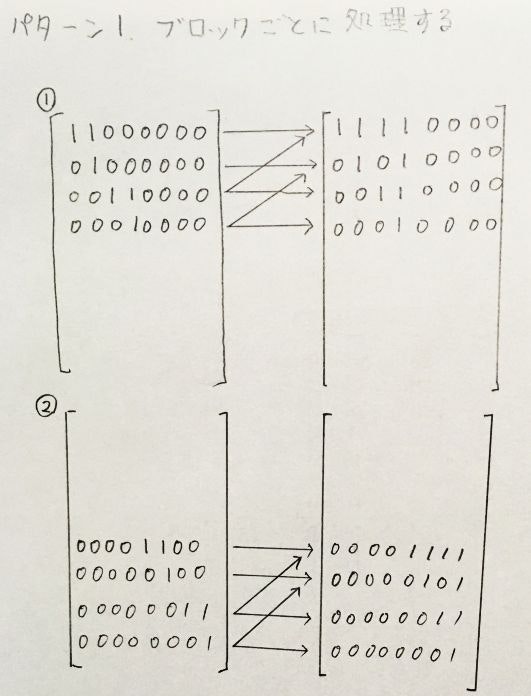
また、このようなバタフライ演算では、塊ごとに処理するループの回し方が次の2通りあります。
ループの段数が浅いうち(演算過程の図の左の方)は、パターン1の回し方だとループ数が非常に多くなり、そこがボトルネックになってしまいます。そのような場合は、パターン2の回し方にすると速度が向上できます。
特に、1番最初のループでは、要素数が$2^{18}$の場合だと、パターン1だとループ回数が$2^{17}$回なのに対し、パターン2だと1回のループで計算が終わり、非常に高速になります。
詳細は、以下の提出コードを見ていただければと思います。
import sys
import numpy as np
def input():
return sys.stdin.readline()[:-1]
# 入力処理
n,m = tuple(map(int,input().split()))
a = np.fromstring(input(), sep=' ', dtype=np.int32)
# 外側ループ回数
k = (max(n,m)-1).bit_length()
# 要素数。FFTと同じ理屈で、2のべき乗にする。
h = 1<<k
# aの要素数を2のベキに切り上げて、後ろに詰める。
# 前の方はゼロ埋めする。
a = np.r_[np.zeros(shape=(h-n,),dtype=np.int32), a]
# ブロックサイズ
s = 2
for i in range(k):
# 高速化の工夫。ブロックサイズが小さい場合は
# 各ブロックの第1要素をまとめて処理、、第2要素をまとめて処理、・・・
# とする。最適な閾値は128か256程度か。
if s<=128:
for j in range(s//2):
ae = a[j :h:s] # a_even 偶数番目の項
ao = a[j+(s//2):h:s] # a_odd 奇数番目の項
ae[:] ^= ao # in-placeな処理
pass
# ブロックサイズが大きい場合は、各ブロックごとに処理する。
else:
for j in range(h//s):
ae = a[j*s : j*s + (s//2)] # a_even 偶数番目の項
ao = a[j*s + (s//2): (j+1)*s] # a_odd 奇数番目の項
ae[:] ^= ao # in-placeな処理
# ループ1回ごとにブロックサイズが2倍になる。
s *= 2
# 出力処理
print(*(a[:m].tolist()))
このコードで実行時間は461msで、記事執筆時点ではPython・PyPyの中で最速となっています。