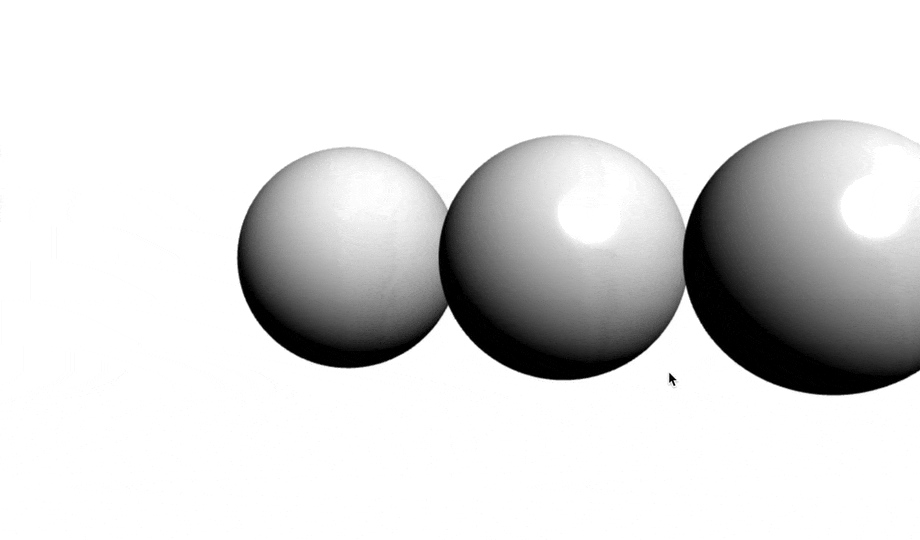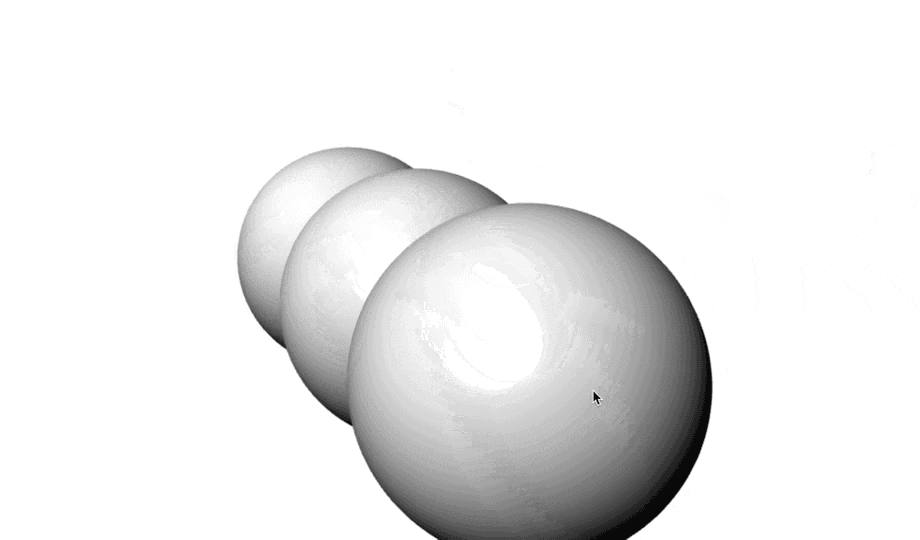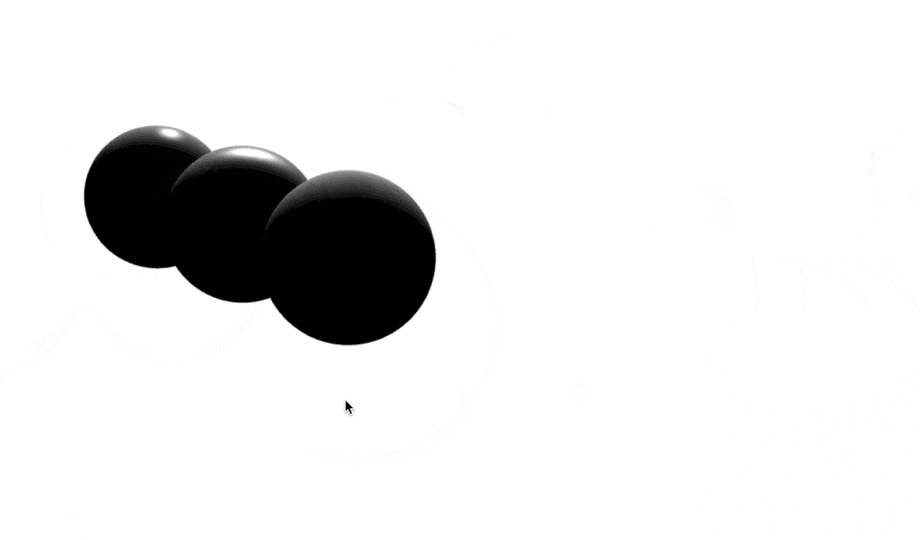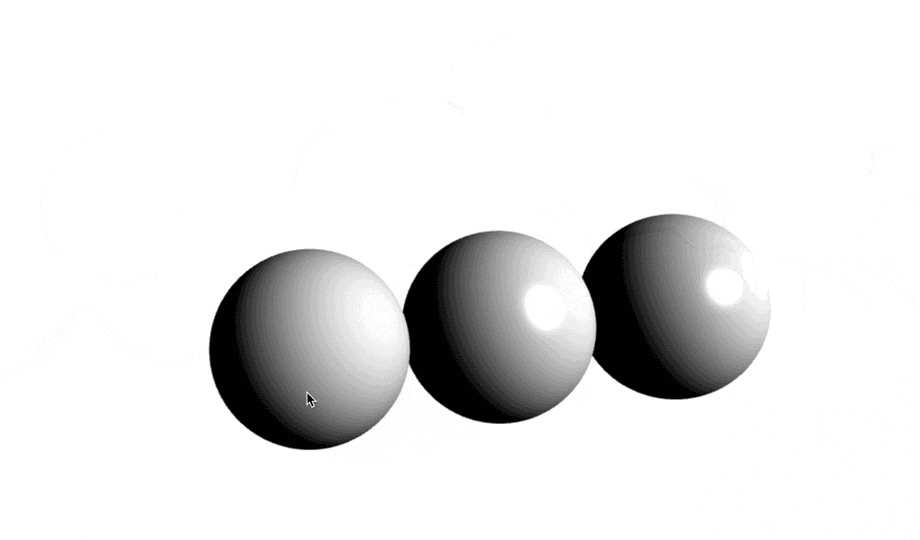12月25日の最後のカレンダーのために書くネタをとりあえず思いつかなかったので、自分の復習も兼ねていくつかのシェーディングモデルを実際に**Grimoire.js**で実装してみた。
ここでは、主にGrimoire.jsの紹介というより、各種シェーディングモデルのまとめのような存在とご理解いただきたい。
今回作ったもの。
みなさん、それぞれどんな式か当てられますか?
実際に動かしたい方は、コチラ
下準備+ランバート
ライブラリを読み込んで球体を表示するだけのhtmlファイルを作成する。
今回はGrimoire.jsをCDNから読み込む。
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title></title>
<script src="https://unpkg.com/grimoirejs-preset-basic/register/grimoire-preset-basic.min.js" charset="utf-8"></script>
</head>
<body>
<script type="text/goml">
<goml>
<import-material typeName="lambert" src="./lambert.sort"/>
<scene>
<camera>
<camera.components>
<MouseCameraControl center="10"/>
</camera.components>
</camera>
<mesh material="new(lambert)" geometry="sphere"/>
</scene>
</goml>
</script>
</body>
</html>
以下のように書いて、lambert.sortを用いてGrimoire.jsで描画する。(.sortはGrimoire.jsのシェーダーファイル)
以下のようにランバート用のシェーダーを書く。
@Pass{
FS_PREC(mediump,float)
varying vec3 vNormal;
# ifdef VS
attribute vec3 position;
attribute vec3 normal;
uniform mat4 _matPVM;
uniform mat4 _matM;
void main(){
gl_Position = _matPVM * vec4(position,1);
vNormal =normalize((_matM * vec4(normal,0)).xyz);
}
# endif
# ifdef FS
@{default:"white",type:"color"}
uniform vec3 color;
@{default:"1,1,1"}
uniform vec3 ld;
void main(){
gl_FragColor = vec4(color * dot(vNormal,normalize(ld)),1);
}
# endif
}
見ての通り、ほとんどGLSLそのままのものにデフォルト値などを指定したり、jsをいじらなくてもシェーダーをある程度扱えるためのGrimoire.jsで扱える仕組みがsortだ。
なお、以下特にことわりのない限りLはライトの方向へのベクトル、Vはカメラの方向へのベクトル、Nは法線を意味する。
これらのすべてのベクトルは正規化されているものとする。
ランバートは一番基本の式だが、要するに以下の式だ。
\mathbb{C}_d = \mathbb{k}_dmax[0,\mathbb{N} \cdot \mathbb{L}]
LとNが正規化されているので、
L \cdot N = |L||N|cos\theta = cos\theta
となり、要するに法線とライトのベクトルの間の角度の余弦によって明るさが決まるという単純な式だ。
Phong鏡面反射
以下のようにPhongのシェーダーをかく。
@Pass{
FS_PREC(mediump,float)
varying vec3 vNormal;
varying vec3 vPosition;
# ifdef VS
attribute vec3 position;
attribute vec3 normal;
uniform mat4 _matPVM;
uniform mat4 _matM;
void main(){
gl_Position = _matPVM * vec4(position,1);
vNormal =normalize((_matM * vec4(normal,0)).xyz);
vPosition = (_matM * vec4(position,1)).xyz;
}
# endif
# ifdef FS
@{default:"white",type:"color"}
uniform vec3 diffuse;
@{default:"white",type:"color"}
uniform vec3 specular;
@{default:100}
uniform float shininess;
@{default:"n(1,1,1)"}
uniform vec3 ld;
uniform vec3 _cameraPosition;
void main(){
float cosine = dot(vNormal,ld);
vec3 dCol = max(0.,cosine) * diffuse;
vec3 cDir = normalize(_cameraPosition - vPosition);
float specAngle = dot(reflect(-ld,vNormal),cDir);
vec3 sCol = vec3(0,0,0);
if(specAngle > 0.){
sCol = pow(specAngle,shininess) * specular;
}
gl_FragColor = vec4(sCol + dCol,1);
}
# endif
}
先ほどのhtmlの中のgomlの部分を以下のように編集し。。。
<goml>
<import-material typeName="lambert" src="./lambert.sort"/>
<import-material typeName="phong" src="./phong.sort"/>
<scene>
<camera>
<camera.components>
<MouseCameraControl center="10"/>
</camera.components>
</camera>
<mesh material="new(lambert)" geometry="sphere"/>
<mesh material="new(phong)" position="2,0,0" geometry="sphere"/>
</scene>
</goml>
先ほどのlambertにより計算されるdiffuse(拡散)光に、さらにspecular(反射)光を付け加えたものです。
特に、この鏡面のような反射光の部分がphongの式によって計算されています。
Rをライト方向Lから入射した反射光を意味するベクトルとすれば、このspecular部分の色は以下のように表せます。
\mathbb{C}_s = \mathbb{k}_s (R \cdot V)^ \alpha
ただし、αは反射度合いを表すshininessを意味します。またRとVのなす角が鈍角になる場合、は0とします。0の0乗が1になっているため、裏面のちょうど0になってしまうところも明るくなってしまうのを避けるためです。
Blinn-Phong鏡面反射
上の式の反射ベクトルを求める部分をハーフベクトルを用いて近似したのが以下になります。
まず、例によってシェーダーを書き...
@Pass{
FS_PREC(mediump,float)
varying vec3 vNormal;
varying vec3 vPosition;
# ifdef VS
attribute vec3 position;
attribute vec3 normal;
uniform mat4 _matPVM;
uniform mat4 _matM;
void main(){
gl_Position = _matPVM * vec4(position,1);
vNormal =normalize((_matM * vec4(normal,0)).xyz);
vPosition = (_matM * vec4(position,1)).xyz;
}
# endif
# ifdef FS
@{default:"white",type:"color"}
uniform vec3 diffuse;
@{default:"white",type:"color"}
uniform vec3 specular;
@{default:100}
uniform float shininess;
@{default:"n(1,1,1)"}
uniform vec3 ld;
uniform vec3 _cameraPosition;
void main(){
float cosine = dot(vNormal,ld);
vec3 dCol = max(0.,cosine) * diffuse;
vec3 cDir = normalize(_cameraPosition - vPosition);
float specAngle = dot(normalize(ld + cDir),vNormal);
vec3 sCol = vec3(0,0,0);
if(specAngle > 0.){
sCol = pow(specAngle,shininess) * specular;
}
gl_FragColor = vec4(sCol + dCol,1);
}
# endif
}
html内のgomlの部分を編集します。
<import-material typeName="lambert" src="./lambert.sort"/>
<import-material typeName="phong" src="./phong.sort"/>
<import-material typeName="blinn-phong" src="./blinn-phong.sort"/>
<scene>
<camera>
<camera.components>
<MouseCameraControl center="10"/>
</camera.components>
</camera>
<mesh material="new(lambert)" geometry="sphere"/>
<mesh material="new(phong)" position="2,0,0" geometry="sphere"/>
<mesh material="new(blinn-phong)" position="4,0,0" geometry="sphere"/>
</scene>
(lambertから一番離れているのがBlinn-phongの式になります)
式的には、以下のようにしてHを出して、先ほどの式を近似しているようなものです。
H = \frac{L + V}{||L+V||}\\
\mathbb{C}_s = \mathbb{k}_s (H \cdot N)^ \alpha
Oren-Nayar法
Lambertのような拡散反射をより、リアルな質感にするために、ラフネス項を考慮したのがOren-Nayar法になります。
以下のようなシェーダーを書きます。
@Pass{
FS_PREC(mediump,float)
varying vec3 vNormal;
varying vec3 vPosition;
# ifdef VS
attribute vec3 position;
attribute vec3 normal;
uniform mat4 _matPVM;
uniform mat4 _matM;
void main(){
gl_Position = _matPVM * vec4(position,1);
vNormal =normalize((_matM * vec4(normal,0)).xyz);
vPosition = (_matM * vec4(position,1)).xyz;
}
# endif
# ifdef FS
@{default:0.3}
uniform float albedo;
@{default:10}
uniform float roughness;
uniform vec3 _cameraPosition;
@{default:"1,1,1"}
uniform vec3 ld;
void main(){
float r = roughness;
float r2 = r * r;
vec3 camDir = normalize(_cameraPosition - vPosition);
float lvd = dot(ld,camDir);
float nld = dot(ld,vNormal);
float nvd = dot(vNormal,camDir);
float s = lvd - nld * nvd;
float t = mix(1.,max(nld,nvd),step(0.,s));
float B = 0.45 * r2 /(r2 + 0.09);
float A = 1.0 + r2 * (albedo/(r2 +0.13) + 0.5/(r2 + 0.33));
float dCol = albedo * max(0.,nld) * (A + B *s/t);
gl_FragColor = vec4(vec3(dCol),1);
}
# endif
}
また、htmlのgomlの部分を以下のように編集します。
<goml>
<import-material typeName="oren-nayar" src="./oren-nayar.sort"/>
<import-material typeName="lambert" src="./lambert.sort"/>
<import-material typeName="phong" src="./phong.sort"/>
<import-material typeName="blinn-phong" src="./blinn-phong.sort"/>
<scene>
<camera>
<camera.components>
<MouseCameraControl center="10"/>
</camera.components>
</camera>
<mesh material="new(oren-nayar)" position="-2,0,0" geometry="sphere"/>
<mesh material="new(lambert)" geometry="sphere"/>
<mesh material="new(phong)" position="2,0,0" geometry="sphere"/>
<mesh material="new(blinn-phong)" position="4,0,0" geometry="sphere"/>
</scene>
</goml>
式としては以下のようになる、
A = 1.0 + \sigma^2\frac{albedo}{\sigma^2 +0.13} + \frac{0.5}{\sigma^2 +0.33})\\
B = \frac{0.45\sigma ^2}{\sigma^2 + 0.09}\\\\
s = L \cdot V - (N \cdot L)(N \cdot V)\\
t = mix(1,max(N \cdot L,N \cdot V),step(0,s))\\
\mathbb{C}_d = albedo* max[0,N \cdot L]*(A+\frac{sB}{t})
それにしてもこの定数たちどこからきたんでしょうね。
まとめ
こんな単純な実験なら少しの変更でWeb上で確認できて案外実験目的でも便利かも?
興味のある方は是非、**チュートリアル**などご参照ください。
ほんとはCook-Torranceの式の中の各式を変えて見た比較とかしたいと思ったのですが(GGXとか)、案外時間がなかったので。そのうちやるかもしれません。