ICLR2022の宝くじ仮説論文

概要

この記事では、ICLR2022の宝くじ仮説論文をまとめます。¹

宝くじ仮説の復習

宝くじ仮説 (Lottery Ticket Hypothesis) は、ICLR2019でFrankleらによって提案された仮説です。

ランダムに初期化された密なニューラルネットワークは、ある部分ネットワークとして当たりくじ(winning ticket)を持つ。当たりくじを初期値として、元の密なニューラルネットワークを学習したのと同様の精度にすることができる。

CVPR2020では、Ramanujanらが、宝くじ仮説よりも強い主張である"強い宝くじ仮説" (Strong Lottery Ticket Hypothesis) と、当たりくじを見つけるための方法であるedge-popup algorithmを提案しました。

十分にパラメータ数の多いランダム初期値のニューラルネットワークは部分ネットワークを持つ。その部分ネットワークは学習せずに元のネットワークと同じ精度を持つ。

Proving the Lottery Ticket Hypothesis for Convolutional Neural Networks

(ICLR2022 Poster)
概要：強い宝くじ仮説の証明。
新規性：CNNの場合で強い宝くじ仮説を証明した。(従来の証明はfully-connected layerのネットワークの場合だった。)

キモ：まず畳み込み1個を刈ったもので任意に近似できることを示して (Lemma 1.2) それを全ネットワークに広げる。
評価：LeNet5で実験した。

On the Existence of Universal Lottery Tickets

(ICLR2022 Poster)
概要：宝くじ仮説の拡張。
新規性：Universal Lottery Ticket (Universal LT) の提案と存在証明をした。

十分にパラメータ数の多いネットワークは、学習無しで部分ネットワークにUniversalな当たりくじを持つ。そのUniversalな当たりくじにMLPを1層加えれば、他のタスクも適用できる。

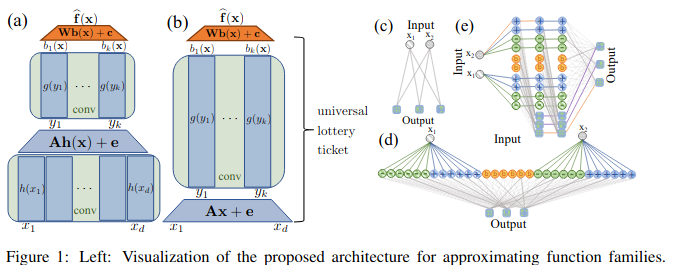
キモ：転移学習のように、MLPを1層加えることによって他のタスクに適用できるようにする。
評価：実験で、Universal LTを構成することができることを示した。

Dual Lottery Ticket Hypothesis

(ICLR2022 Poster)
概要：Dual Lottery Ticket Hypothesis (DLTH) の提案
新規性：当たりくじを見つけるのに学習が必要ない方法を提案した。

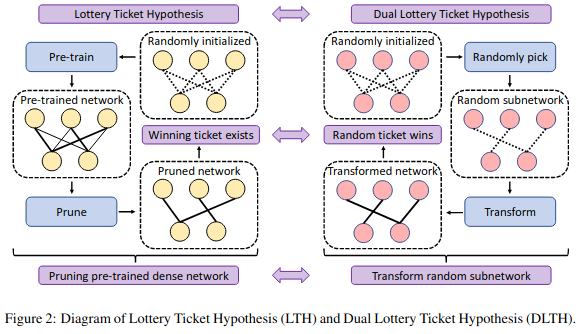
キモ：DLHTを実証するために、当たりくじを見つけるアルゴリズムRandom Sparse Network Transformation (RST)を提案した。

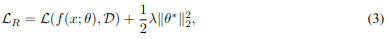
$\lambda$をだんだん大きくする。

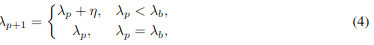
評価：ResNetとCIFARで、学習ありの方法相当まで刈れることを示した。

Peek-a-Boo: What (More) is Disguised in a Randomly Weighted Neural Network, and How to Find It Efficiently

(ICLR2022 Poster)
概要：PaB. 強い宝くじ仮説で、当たりくじを効率的に見つける方法。
新規性：強い宝くじよりも高性能なネットワーク (disguisedなnetwork) をedge-popupアルゴリズムよりも効率的に見つけられる方法を提案した。
キモ：PaBのネットワーク探索においては、枝刈り後、符号のみを入れかえる (unmask) 処理を入れることによってネットワークを探索する。

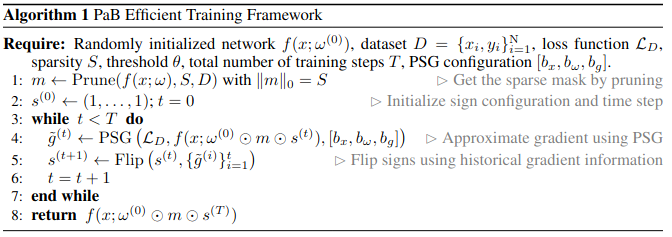
評価：ResNet, CIFARで実験した。

1. 画像や数式は論文から引用しています。 ↩