簡単なDC電流ソルバーを書いてみる

はじめに

この記事はCompetitive Programming (2) Advent Calendar 2019の23日目の記事となります．
電気抵抗をいくつか直列・並列につないだ回路の各抵抗に流れる電流や合成抵抗はいくつになるかというのを計算するDC電流ソルバーを書いてみました．
（現在の競技プログラミングではほとんど出題されないですが，グラフと計算なのでまぁいいかなと）

DC電流ソルバー

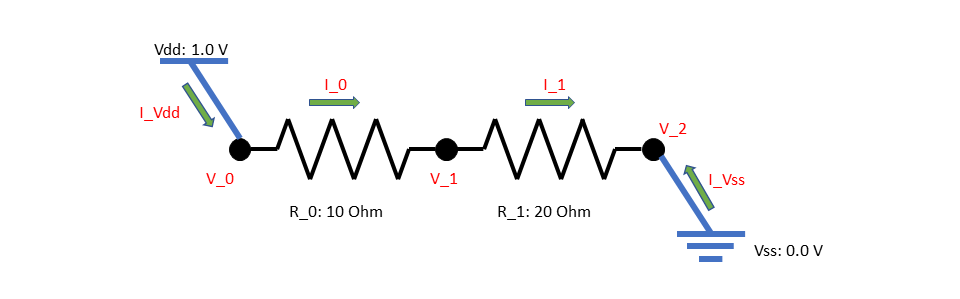
例えば，各抵抗が1.0Ωの抵抗を組み合わせて作った次のような抵抗回路の合成抵抗が知りたくなったとします．

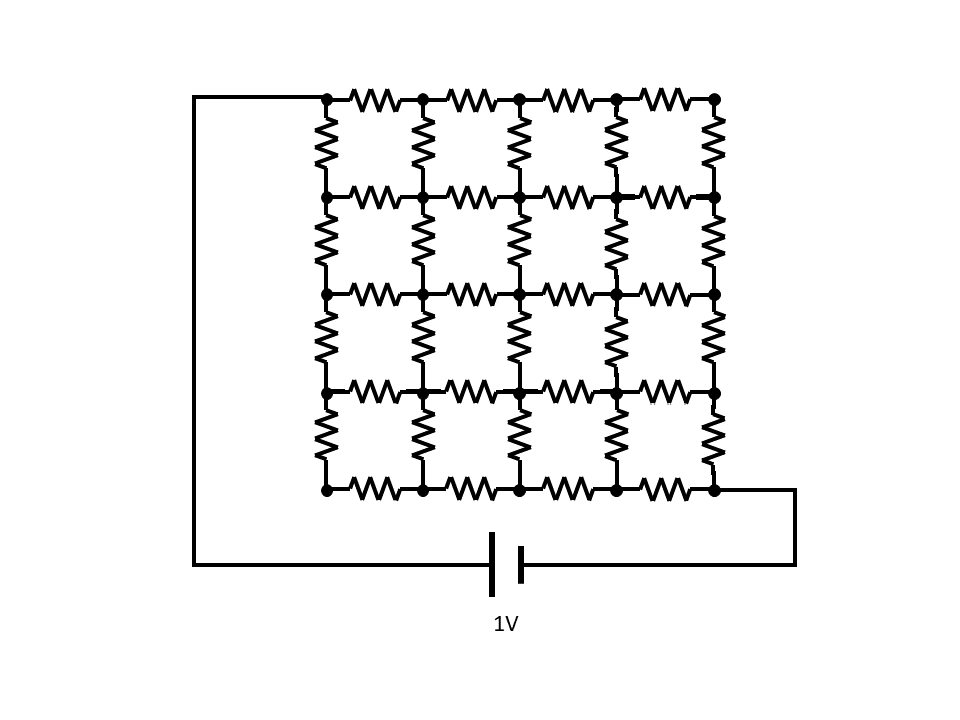
見た目はシンプルなのに実際に計算しようとするととても大変なので，これを計算するプログラムをこの記事ではDC電流ソルバーと呼ぶことにします．前提としては

• 各抵抗値はすべて既知の値
• どこかに電源が接続されている
• 時間要素はなく，定常的に流れるDC電流を計算したい

解き方

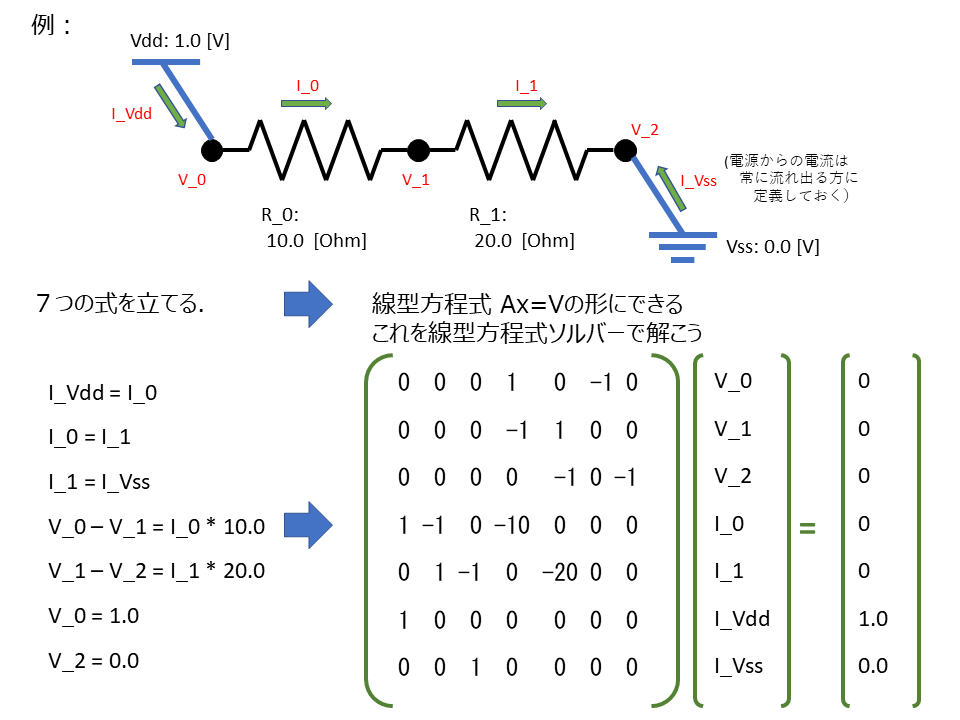
キルヒホッフの電圧則・電流則に従って立式した連立方程式を解くことで，各ノードの電位や各抵抗の電流を求めることができます．そのために適切に変数を定義する必要があります．

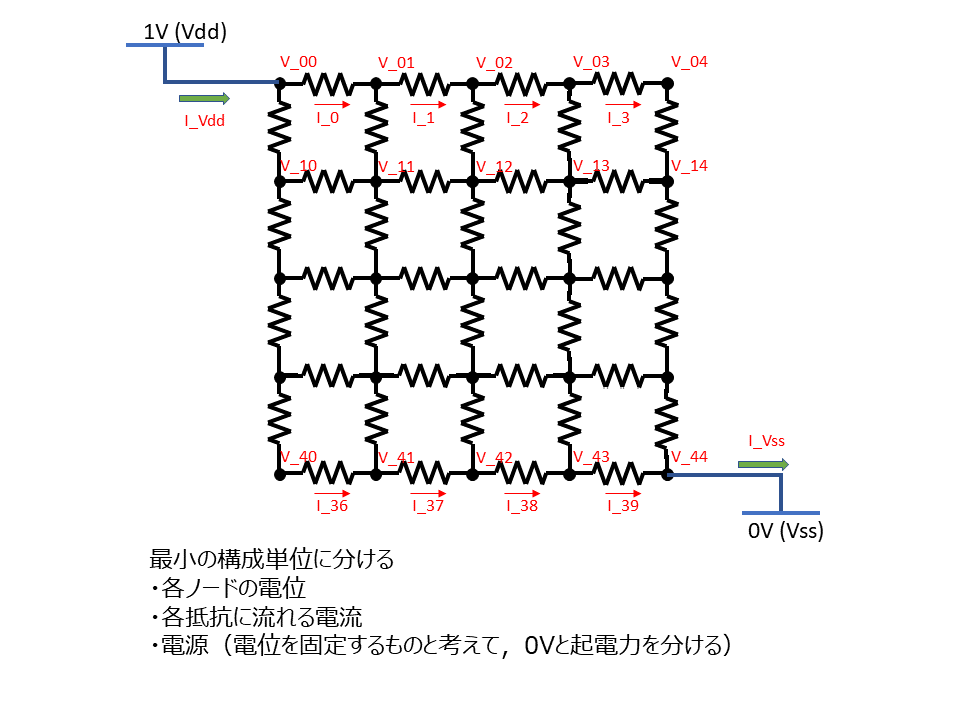
赤字の部分を変数として立式します．
最終的に線型方程式に帰着されるため，最小限の未知の要素を変数にします．
高校の物理の授業や試験ではこのように未知変数の多い系の電流計算はまず出題されないですが，変数が多いと1次独立な式をいくつ立式すべきかというところに実装上の工夫が要ります．電源からの接続をうまく変数として考えることで，次のように必要充分な式を立式することができます．

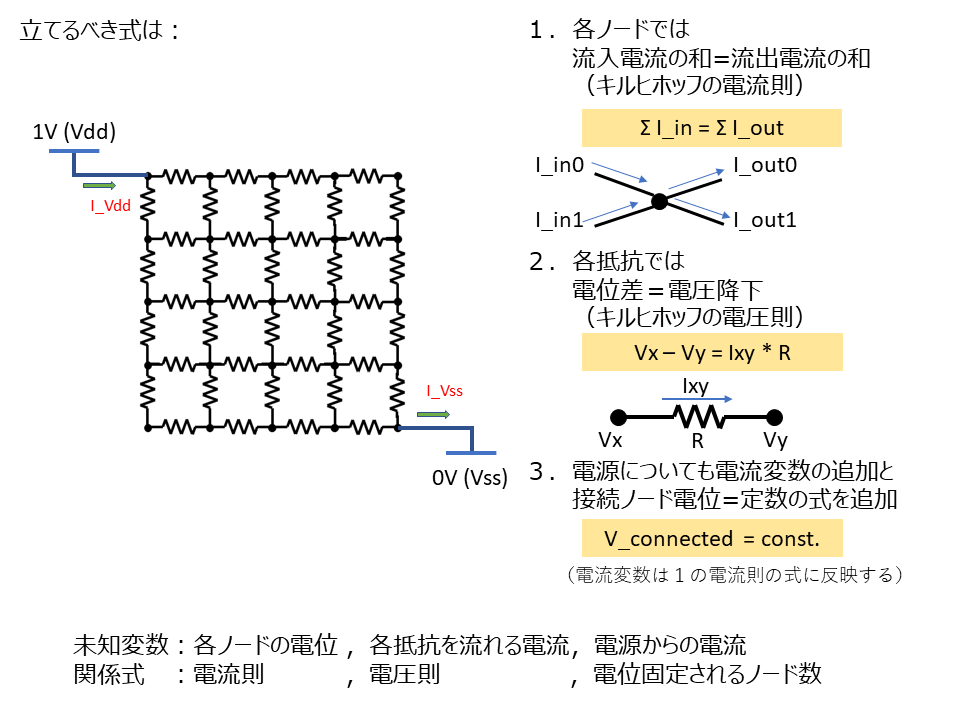
定義した変数の数と同じ数の式が得られます．ポイントは電源をつながないと得られた式が線型独立にならないというところと，電源をつなぐノードの数をいくつ増やしても（電源同士をショートさせない限りは）線型独立な式が得られるというところです．（帰納的に証明できる（はず））

例

例えばこのような単純な直列抵抗の場合

• ノードに流入する電流に関する式を３つ
• 各抵抗での電圧低下に関する式を２つ
• 電源の接続に関する式を２つ

の合計7つを以下の様に立式できます．

Pythonで実装

手軽に使える線型ソルバーがあるのでPythonで書くことにします．ソルバーを書くにあたって次の方針で

• ノード数はインスタンス化時に固定する
• 抵抗定義は（どのノードから，どのノードへ，抵抗値）でインスタンスに登録する
• 電源は複数使用できるように，（電源名，供給電位）で定義する
• 定義した電源をどのノードに接続するかをインスタンスに登録
• call solve()！

ソースはGitHubに置きました．大体こんなかんじ

DCsolver.py

# coding: utf-8
import sys
import time
import numpy as np
from collections import deque

class DCsolver:

    def __init__(self, nodenum):
        # ソルバ―
        self.linear_solver = np.linalg.solve

        # ノード数は固定する．抵抗数とバイアス接続数は更新する
        self.n_node = nodenum
        self.n_res = 0
        self.n_bias_probe = 0

        # 抵抗： 始点，終点，抵抗値
        self.res_from = []
        self.res_to = []
        self.res_value = []

        # 電源： virtual connectするため，名前でアクセスするようにする
        self.bias_name = []
        self.bias_level = []
        self.bias_index = dict() # dict<string,int>

        # Bias supplied (-1: not biased)
        self.biased = [-1] * self.n_node
        # 各バイアスがどのノードにprobeしているかを計算時に確定する
        self.bias_from = None
        self.bias_to = None

        # 1次方程式 A*X=V を解く 
        self._A = None
        self._V = None
        self._X = None 

        # result
        self.node_voltage = None
        self.node_current = None
        self.bias_total_current = None
        self.bias_current_per_node = None
        self.res_current = None

    def add_resistance(self, node_from, node_to, res_value):
        # node_from から node_to へ 抵抗値 res_value の抵抗をつなぐ
        # 　電流の向きをこの向きで定義する
        assert res_value > 0 , "inhibit res_value <= 0"
        self.res_from.append(node_from)
        self.res_to.append(node_to)
        self.res_value.append(res_value)
        self.n_res += 1

    def define_bias(self, bias_name, bias_level=0.0):
        if bias_name in self.bias_index:
            idx = self.bias_index[bias_name]
            self.bias_level[idx] = bias_level
        else :
            idx = len(self.bias_name)
            self.bias_index[bias_name] = idx
            self.bias_name.append(bias_name)
            self.bias_level.append(bias_level)

    def supply_bias_to_node(self, bias_name, node_to):
        # 1つのノードに複数バイアスがアクセスするのを禁止して，最も新しい設定を反映する
        assert bias_name in self.bias_index, \
            "{0} is not defined, please define before supply".format(bias_name)
        idx = self.bias_index[bias_name]
        # 既にバイアスが供給されている場合，警告する．
        if self.biased[node_to] != -1:
            print("bias on node:{0} is changed: {1} --> {2} ".format(
                node_to, self.bias_name[self.bias_index[self.biased[node_to]]], bias_name
            ))
            self.biased[node_to] = idx
        else :
            self.biased[node_to] = idx
            self.n_bias_probe += 1

    def _create_matrix(self):
        # (A, V) を定義する
        nv = self.n_node
        nr = self.n_res
        nb = self.n_bias_probe

        # 最終的なバイアス条件設定をリストアップしてインデックス付け
        self.bias_from = []
        self.bias_to = []
        for i in range(nv):
            if self.biased[i] != -1:
                self.bias_from.append(self.biased[i])
                self.bias_to.append(i)
        assert nb == len(self.bias_from)

        # 行列サイズ = ノード数 + 抵抗数 + バイアス供給パス数
        # 未知変数
        #  [0...nv-1]: ノードiの電位
        #  [nv...nv+nr-1] : 抵抗の電流
        #  [nv+nr...n-1] : バイアス供給パスの電流
        n = nv + nr + nb
        mat = np.zeros((n,n))
        vec = np.zeros(n)

        # Kirchhoff's Current Law （各ノードの outgo と income の総和は0）
        #  i 行目([0...nv-1])の式はノードiに関する電流の和
        #  抵抗jに流れる電流は from[j]のoutgo　to[j]のincomeとしてカウントされる
        for j in range(nr):
            mat[self.res_from[j]][nv + j] = 1
            mat[self.res_to[j]][nv + j] = -1

        # Kirchhoff's Voltage Law （各抵抗の電圧降下は電位差）
        #  nv+j 行目([nv...nv+nr-1])の式は抵抗j に関する電流の和
        for j in range(nr):
            mat[nv + j][self.res_from[j]] = 1
            mat[nv + j][self.res_to[j]] = -1
            mat[nv + j][nv + j] = -self.res_value[j]

        # バイアス定義の式
        #  bias_from[i] の電位がbias_level['bias']に固定される．（KVLパートに追加）
        #  bias_to[i]に電源からの電流が流入する (KCLパートに追加)
        for j in range(len(self.bias_from)):
            mat[nv + nr + j][self.bias_to[j]] = 1
            vec[nv + nr + j] = self.bias_level[self.bias_from[j]]
            mat[self.bias_to[j]][nv + nr + j] = -1

        # Biasがつながっていないノードがないかチェックする（floating nodeは非許容にする）
        self.check_connention()
        return mat, vec

    def check_connention(self):
        E = [[] for i in range(self.n_node)]
        for i in range(self.n_res):
            E[self.res_from[i]].append(self.res_to[i])
            E[self.res_to[i]].append(self.res_from[i])

        q = deque()
        vis = [False] * self.n_node
        for node in self.bias_to:
            q.append(node)
        while(len(q) > 0):
            now = q.popleft()
            vis[now] = True
            for nxt in E[now]:
                if not vis[nxt]:
                    q.append(nxt)

        floating_node = []
        for node in range(len(vis)):
            if not vis[node]:
                floating_node.append(node)
        if len(floating_node) != 0:
            print("Some floating node(s) exist:\nnode(s):\n{0}\n--> Aborted".format(floating_node))
            sys.exit(0)




    def solve(self):
        A, V = self._create_matrix()
        X = self.linear_solver(A, V)
        X = np.array(X)
        self._A = A
        self._V = V
        self._X = X

        self.node_voltage = X[0:self.n_node]
        self.res_current = X[self.n_node: self.n_node + self.n_res]        
        self.bias_current_per_node = dict()
        self.bias_total_current = dict()

        for bname in self.bias_name:
            self.bias_current_per_node[bname] = []
            self.bias_total_current[bname] = 0.0
        for i in range(self.n_bias_probe):
            bname = self.bias_name[self.bias_from[i]]
            self.bias_current_per_node[bname].append( (self.bias_to[i], X[self.n_node + self.n_res + i]) )
            self.bias_total_current[bname] += X[self.n_node + self.n_res + i]

        # ノードの電流はoutgoのみを計算（（Σ|outgo|+Σ|income|)/2 で計算する）
        self.node_current = np.zeros(self.n_node)
        for i in range(self.n_res):
            self.node_current[self.res_from[i]] += np.abs(self.res_current[i])
            self.node_current[self.res_to[i]] += np.abs(self.res_current[i])
        for bname in self.bias_current_per_node:
            for node, cur in self.bias_current_per_node[bname]:
                self.node_current[node] += np.abs(cur)
        self.node_current /= 2.0

    def print_result_summary(self, showCoef = False):
        if showCoef:
            print('A',self._A)
            print('V',self._V)
            print('X',self._X)
        print('node_voltage\n:{0}\n'.format(self.node_voltage))
        print('res_current\n:{0}\n'.format(self.res_current))
        print('node_cur\n:{0}\n'.format(self.node_current))
        print('bias_cur\n:{0}\n'.format(self.bias_total_current))
        print('bias_cur_per_node\n:{0}\n'.format(self.bias_current_per_node))

異電源が同一ノードに接続されないようにsupply_bias_to_nodeでチェックをかけているところと，供給されていないノードが無いように行列を生成するタイミングでcheck_connentionを入れているところがポイントでしょうか（行列が退化していると線型ソルバーがエラーを吐くだけですが）
前処理の時間計算量は$O(ノード数＋抵抗数＋電源接続数）$になっているので，計算自体は線型ソルバーの計算量でほぼ律速するはずです．

実際に使ってみる

実際に使ってみます．まずは簡単な例．

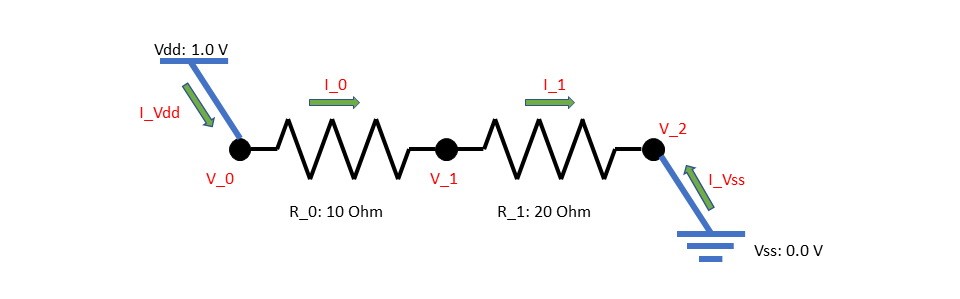
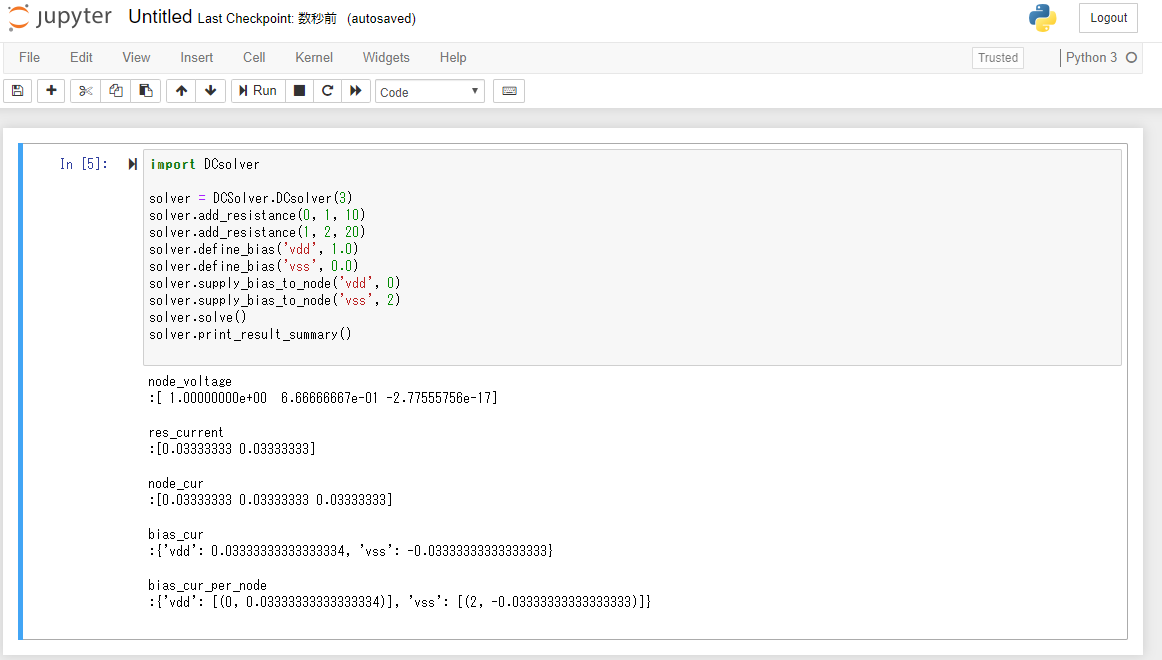
ノード数3つに抵抗2つを直列に接続した例です．
合成抵抗はVddから出る電流の逆数ですが，Vdd電流は0.0333...Aで確かに30Ωになっています．

次に2つ目の抵抗を並列にしてみます．

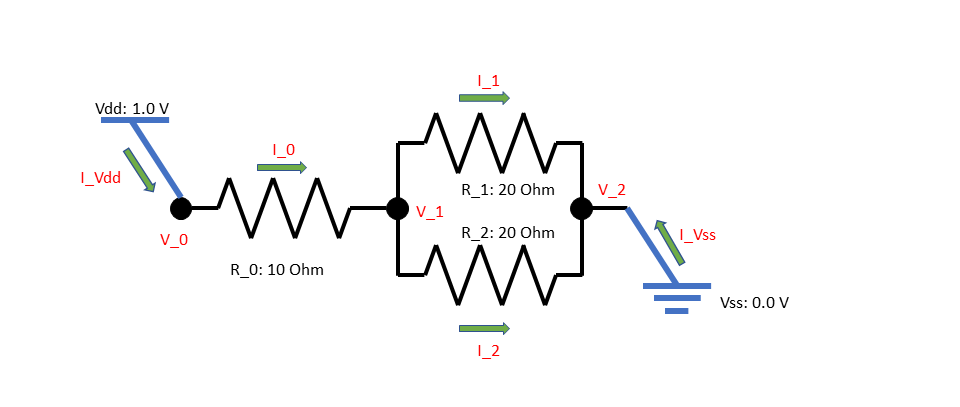
ノード1からノード2へ2つ抵抗を定義してやる形になります．
合成抵抗が20Ωになりますが，Vdd電流は0.05Aで確かになっています．

少し複雑な例だと

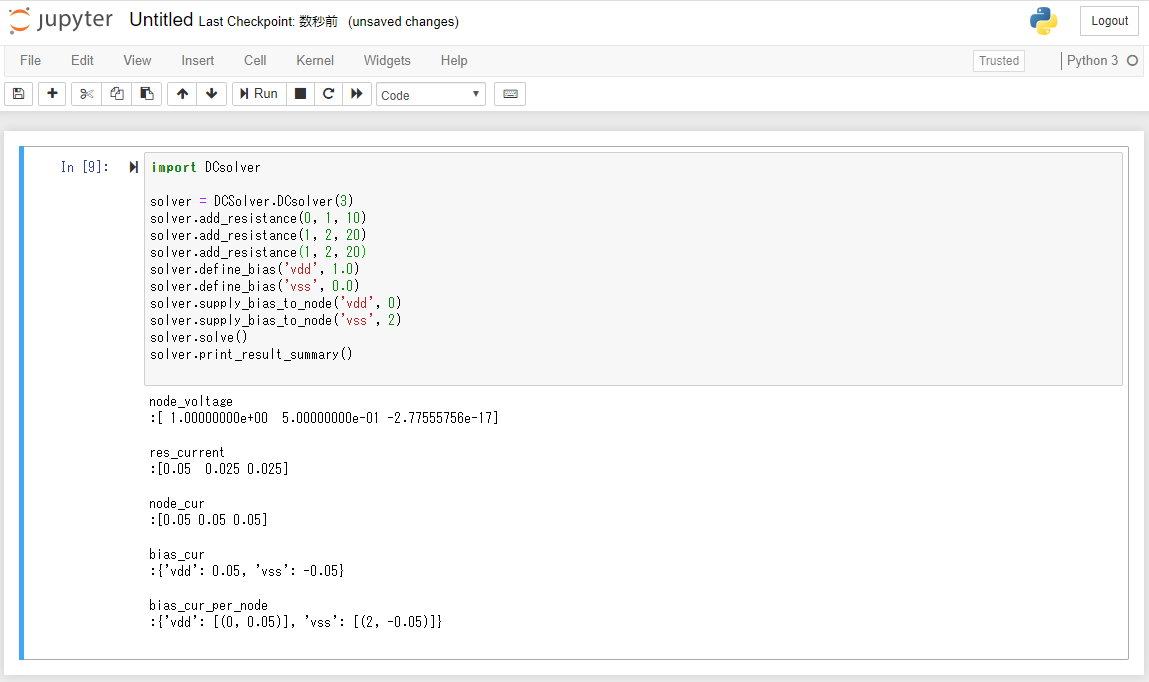
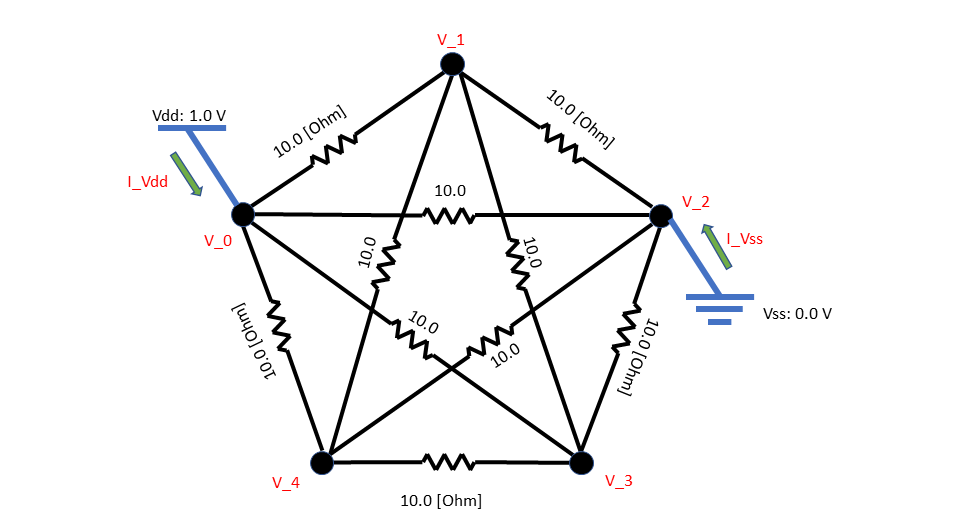
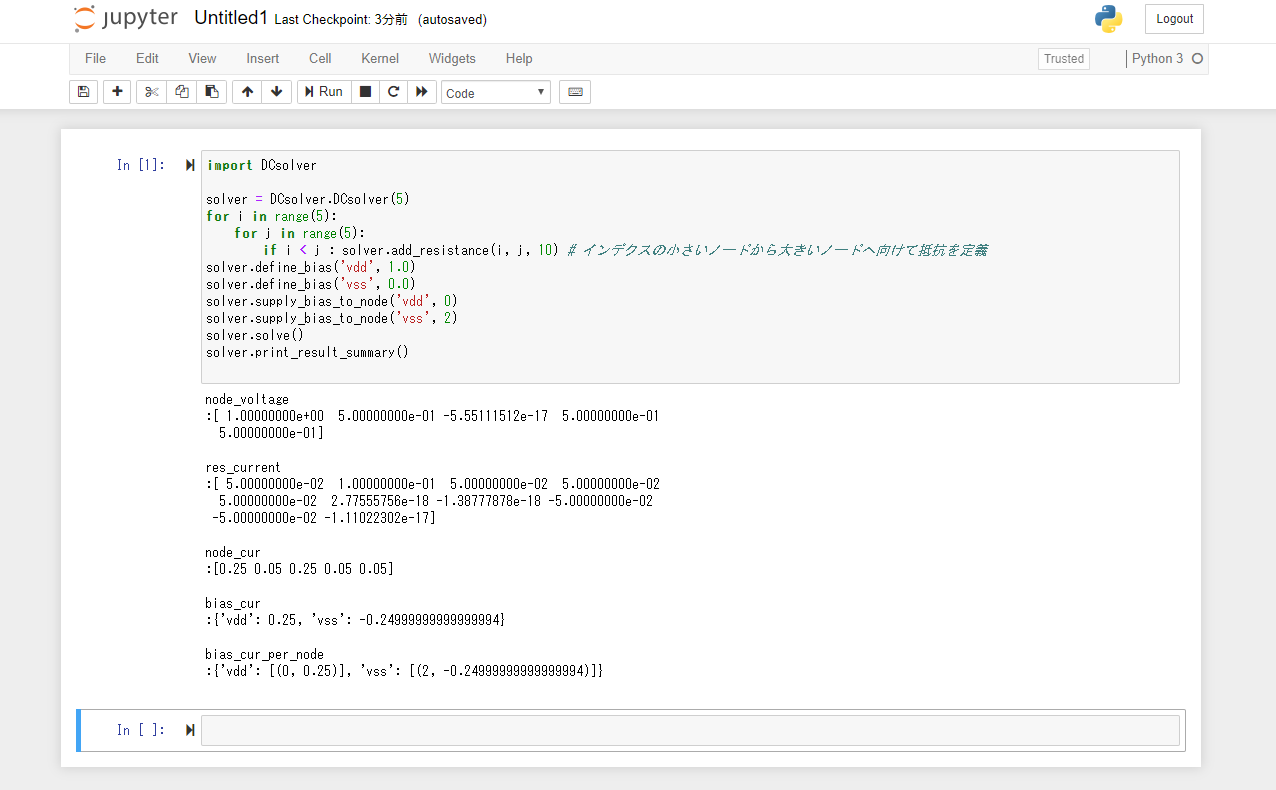
直感的には回り込み要素がどれくらいあるのかわからないですが，Vdd電流は0.25Aで4Ωになるようですね．
V1,V3,V4は同電位になっているので，事実上縮退していて（1/20 + 1/10 + 1/(5+5))^-1 になっているのですね．

メッシュの抵抗

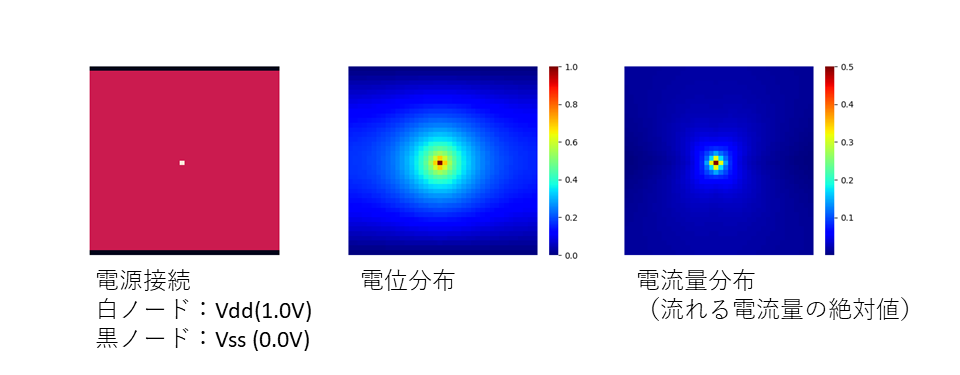
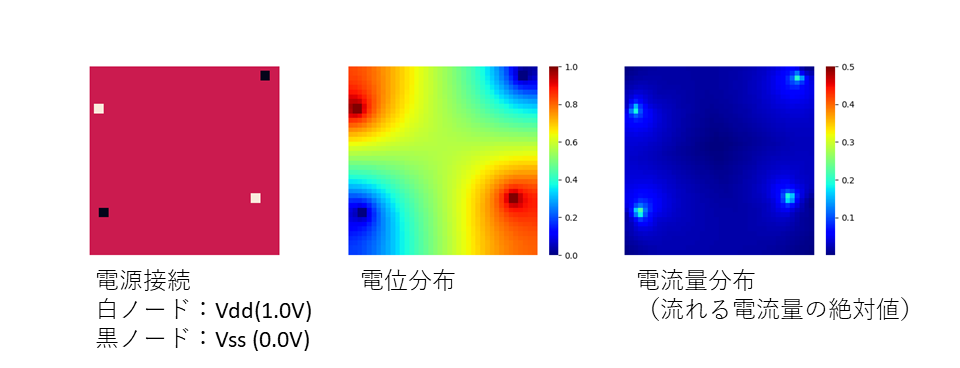
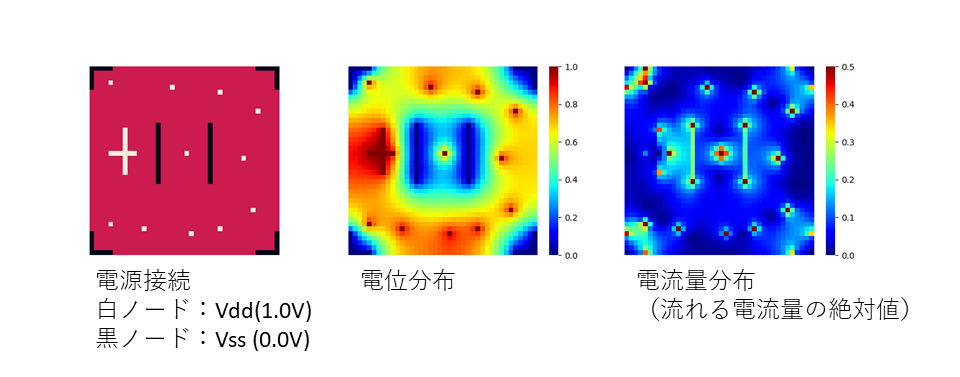
ソルバーを使ってメッシュのノードに適当に電位を供給したときの電位の分布や電流の分布などをいくつか．
50×50のノードからなるメッシュで，隣接ノード間で1Ωで接続しています．

• sample1
  

• sample2
  

• sample3
  

計算時間ですが，同じ回路構造でも電源の接続の仕方，数によって大きく異なるようで，sample1,sample3は1秒かからず計算できましたが，sample2は200秒近くかかりました．
変数の数が(50×50) + 2*(50 * 49) + 電源接続数で7400以上になるので，それでも速いという気はします．
（こちらはscipyの疎行列ライブラリをつかいました）
直接法で求めているので，間接法（反復法）で求めればもう少し速くはなりそうです（今回は未検証）．
コードなどはここに置きました．

終わりに

これからも楽しい電気回路ライフを！