$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
何を書いてあるか
- 量子コンピューターで使う「量子ビット」は「ブロッホ球」を考えると見える化できる
- なぜ「ブロッホ球」で「量子ビット」を見える化できるかは、2 状態の重ね合わせを、複素数の係数で展開してやると導ける
筆者は量子コンピューターについては初心者 of 初心者です。
間違い、もっとわかりやすい表現などは指摘していただけると喜びです
量子的な計算はなにをしているか
以降「量子ゲート型量子コンピュータ」のことを勝手に「量子コンピュータ」と呼称しながらすすめていきます
量子コンピューターでの計算をものすごくざっくり言うと(怒られそうだけど)
-
量子ビットの状態を -
量子ゲート(量子演算子)で操作しながら - 量子ゲートの組み合わせである
量子回路を用いて - 特定のアルゴリズムに従って計算する
ことをしています。
従来のコンピューターでの計算は(これまた怒られそうだけど)
-
ビットの状態を -
論理ゲートで操作しながら - 論理ゲートの組み合わせである
論理回路を用いて - アルゴリズムに従って計算する
ことをしていることとの対比を考えるとそこまで違和感はありません。
以降は以下のように呼称します
- 従来のコンピュータでの計算を「古典的な計算」
- 量子コンピュータでの計算を「量子的な計算」
- 従来のコンピュータで扱うビットを「古典ビット」
入出力と量子的な計算
一旦、量子ビットと古典ビットの違いをおいておいて、計算の入出力を考えると古典と量子で明確な違いが出てきます。
- 古典的な計算は、入力が同じなら出てくる出力は一緒
- 量子的な計算は、入力が同じでも出てくる出力が異なる
どういうことなのか、極端なイメージ例ですが
足し算の回路を組んで 1 + 1 を 1000 回実行すると
- 古典的な計算 : 1000 回とも 2 が出力される
- 量子的な計算 : 800 回 2 が出力されて、200 回は別の値が出力される
ということが起こりえます。
これだけみると量子コンピュータ不要では?と思ってしまいますが
それはこの計算課題(足し算)では恩恵が得にくいからです。
例えば ある計算課題 を解くためのアルゴリズムを 100 回実行すると
- 古典的な計算 : 実時間内に計算が終わらず出力が得られない。
- 量子的な計算 : 実時間内で 70 回 は「出力1」が得られて、30 回は別の複数の出力が得られる
そんな計算があったら量子コンピューターの恩恵がでかいですよね
上記はざっくりとした比喩ですが、大きな桁数の因数分解に使われるアルゴリズムなどが、量子コンピューターが有効な計算課題として捉えられています。
なぜ量子的な計算では同じ入力で出力が異なるのか
ここで、古典ビットと量子ビットの性質の大きな違いが関与してきます。
古典ビットで 1 の状態を取るものは、何度観測しても 1 です。
量子ビットも 1 の状態として出力された(観測された)ものは、操作をしない限り何度観測しても 1 です。
10 回観測したら 10 回とも 1 が観測されます。
しかし、計算過程の「重ね合わせ状態にある量子ビット」は、観測するたびに確率的に状態が決まます。
10 回観測したら 8 回は 1 で、2 回 は 0 を観測するということが起こるのです。
古典ビット
- 入力時の状態 : 0 or 1 のどちらかの状態が確定
- 計算中の状態 : 0 or 1 のどちらかの状態が確定
- 出力時の状態 : 0 or 1 のどちらかの状態が確定
量子ビット
- 入力時の状態 : 0 or 1 のどちらかの状態か確定
- 計算中の状態 : 0 と 1 が重ね合わさった状態
- 出力時の状態 : 0 or 1 のどちらかの状態が確定
古典ビットはどの過程でも、0 or 1 のどちらかが確定していてます。
論理ゲートをたどれば、入力が同じなら出力も同じになります。
どの計算過程で計算を中断して、古典ビットの状態を観測しても 10 回 観測したら 10 回とも同じ状態が観測されます
しかし、重ね合わせ状態にある量子ビットは、10 回観測したら 8 回は 1 で、2 回 は 0 を観測するということが起こりえます。
そのためたとえ同じ入力、同じ量子回路でも出力が異なるということが起こってきます。
この「重ね合わせ状態にある量子ビット」も含めて可視化するために「ブロッホ球」という考え方を使います。
量子ビットを見える化する
古典ビットの「見える化」は簡単です。0, 1 を書いておけばいいです。
しかし量子ビットの「見える化」は難しいです。0 と 1 が重ね合わさった状態で計算されるからです。
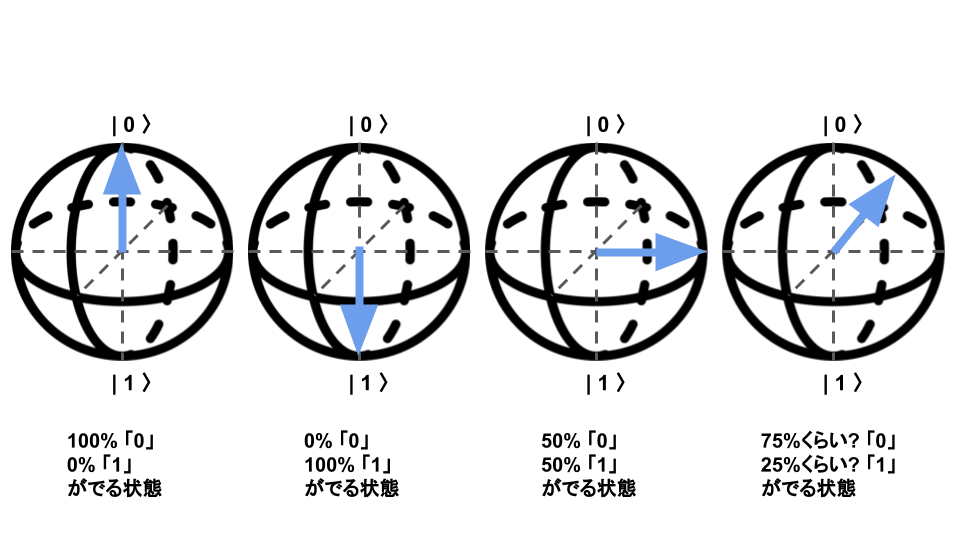
- [A] 10 回観測したら 10 回とも 1
- [B] 10 回観測したら 8 回は 1 で、2 回 は 0
- [C] 10 回観測したら 5 回は 1 で、5 回 は 0
- [D] 10 回観測したら 10 回とも 0
などの量子ビットを区別し、さらに量子ゲートの操作で [A] → [C] に変換するなどをどう表現するのか。
「ブロッホ球」という名前の通り、量子ビットを表現するには球を使います
Z 軸からの角度によって、観測される確率が異なります。
量子ゲートを動作させると、この矢印がぐるっとどこかに移動します。
以上です。
数式で理解する「量子ビット」
しかし、納得できないですよね。いきなり球がでてきて、これが量子ビットを表しますと言われても。。
なんで「ブロッホ球」で量子ビットの状態を表現できたことになるのか?という疑問があったので数式で追っかけてみました。
観測したら 100% 「0」がでる状態を
$$
\ket{\psi} = \ket{0}
$$
観測したら 100% 「1」がでる状態を
$$
\ket{\psi} = \ket{1}
$$
と表すと「0」と「1」の 2 状態の重ね合わせは以下のように書き出せます
$$
\ket{\psi} = \alpha\ket{0} + \beta\ket{1}
$$
ここで $\alpha$ , $\beta$ は複素数で
$$
\alpha^2 + \beta^2 = 1
$$
を満たす
- $\alpha^2$ は $\ket{0}$ を観測する確率
- $\beta^2$ は $\ket{1}$ を観測する確率
を表します。
ここから、$\alpha$ , $\beta$ を複素数とわかるように書き換えます
a, b, $\theta_1$, $\theta_2$ を実数の定数として
$e^{i\theta} = \cos\theta + i\sin\theta$ を利用して
$$
\alpha = a e^{i\theta_1} \
\beta = b e^{i\theta_2} \
$$
と置くと
$$
\begin{align}
\ket{\psi} &= \alpha\ket{0} + \beta\ket{1}\
&= a e^{i\theta_1}\ket{0} + b e^{i\theta_2}\ket{1}\
&= e^{i\theta_1}(a \ket{0} + b e^{i(\theta_2 - \theta_1)}\ket{1})\
&= e^{i\theta_1}(a \ket{0} + b e^{i\phi}\ket{1})
\end{align}
$$
ここで
$$
\phi = \theta_2 - \theta_1\
\delta = \theta_1
$$
と置いた
さらに $\alpha^2 + \beta^2 = 1$ の条件に
$\alpha = a e^{i\theta_1}$, $\beta = b e^{i\theta_2}$ を代入すると
$$
a^2 + b^2 = 1
$$
が得られる。ここから
$$
a = cos\theta\
b = sin\theta \
0 \leq \theta < \frac{\pi}{2}
$$
と置くと
$$
\ket{\psi} = e^{i\delta}(cos\theta\ket{0} + sin\theta e^{i\phi}\ket{1}) \
0 \leq \theta < \frac{\pi}{2} \
0 \leq \delta < 2\pi
$$
$\theta$ の範囲については物理的な制約がかかっている。仮に $\theta = \pi$ を考えてみると
$$
\theta = 0 \quad:\quad \ket{\psi} = e^{i\delta}\ket{0}\
\theta = \pi \quad:\quad \ket{\psi} = -e^{i\delta}\ket{0}
$$
これらは物理的に同じ状態を表す
こういった対称性から、$0 \leq \theta < \frac{\pi}{2}$ になっている
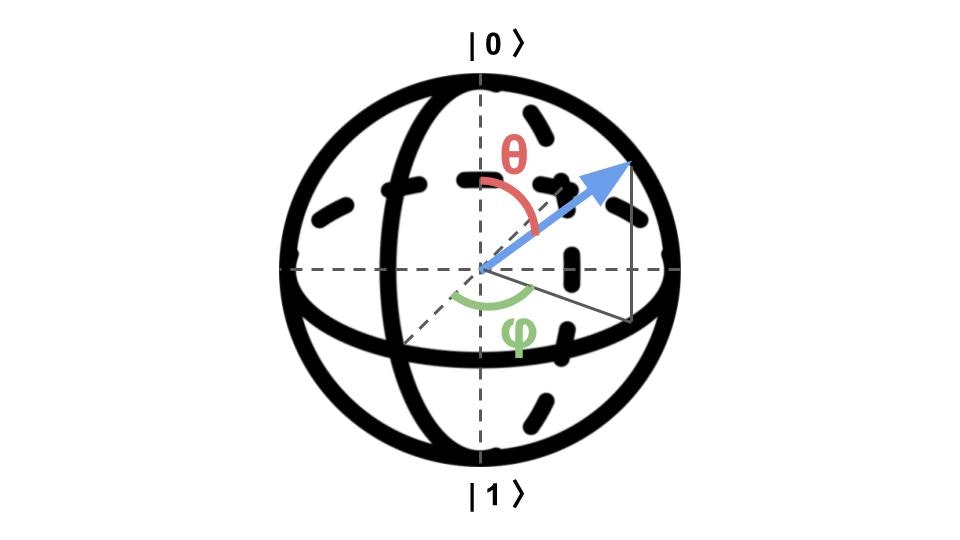
球として表現するために数式をいじると
$$
\ket{\psi} = e^{i\delta}(cos\frac{\theta}{2}\ket{0} + sin\frac{\theta}{2} e^{i\phi}\ket{1}) \
0 \leq \theta < \pi \
0 \leq \delta < 2\pi
$$
と表現できる。$e^{i\delta}$ を無視してこの式を図示すると、以下のように球で表現できる。
ここまでただ式変形をしてきただけなので矢印は、2 つの状態をとる量子状態の重ね合わせのすべて(ただし $e^{i\delta}$ の自由度を無視)して表現できている。
注意点ですが、ブロッホ球はあくまで「便宜上可視化」したものにすぎません。実際に測定できるのは |0> か |1> のどちらかです。