[python]scipyで距離行列を作る

目標

行列$M$の行$m_i, m_j$の距離からなる距離行列$dist(M)$を作る。

M = 
\begin{pmatrix}
m_1 \\
m_2 \\
\vdots \\
m_k
\end{pmatrix}\\

dist(M) = 
\begin{pmatrix}
dist(m_1,m_1) & dist(m_1,m_2) & \dots & dist(m_1,m_k)\\
dist(m_2,m_1) & dist(m_2,m_2) & & \vdots\\
\vdots & & \ddots & \\
dist(m_k,m_1) & \dots & & dist(m_k,m_k)
\end{pmatrix}

ソース

import numpy as np
from scipy.spatial import distance

M = np.random.randint(0, 10, (5, 2))
dist_M = distance.cdist(M, M, metric='euclidean')

# M =>
# [[8 7]
#  [8 0]
#  [8 3]
#  [9 6]
#  [3 4]]

# dist_M =>
# [[ 0.          7.          4.          1.41421356  5.83095189]
#  [ 7.          0.          3.          6.08276253  6.40312424]
#  [ 4.          3.          0.          3.16227766  5.09901951]
#  [ 1.41421356  6.08276253  3.16227766  0.          6.32455532]
#  [ 5.83095189  6.40312424  5.09901951  6.32455532  0.        ]]

おまけ

import seaborn as sns
import matplotlib.pyplot as plt

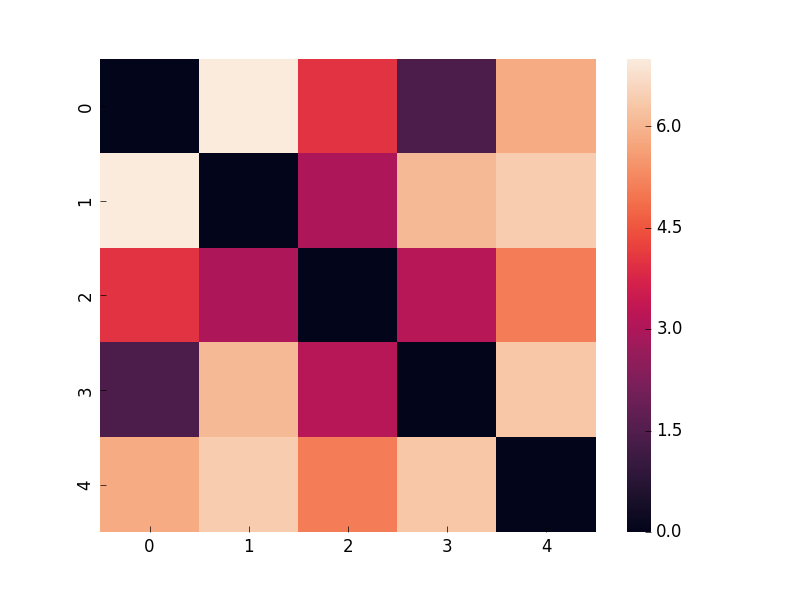
sns.heatmap(dist_M)
plt.show()

$m_0$と$m_3$の距離が小さいことが視覚的にもわかりやすくなります。

参考

https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.distance.cdist.html
https://seaborn.pydata.org/generated/seaborn.heatmap.html