pythonでNMF(非負値行列因子分解)を実装する

NMFとは

"Non-negative Matrix Factorization"のこと。
各要素が非負であるような行列$M \in \mathbb{R}^{m \times n}$に対して

M \approx UV^T\\
s.t. \qquad U \in \mathbb{R}^{m \times k},\;V\in \mathbb{R}^{n \times k},\;k < min(m, n)

を満たすような$U, V$(ただし各要素は非負)を生成する手法。

更新式

以下のような更新式を適当な回数適用することで$U, V$が得られる。

import numpy as np

def update_uv(M, U, V):
    U = U * np.dot(M, V) / np.dot(np.dot(U, V.T), V)
    V = V * np.dot(U.T, M).T / np.dot(U.T, np.dot(U, V.T)).T
    return U, V

$U, V$の初期値はランダムな非負の行列。
dotは行列の積、『*』『/』は要素ごとの乗算、除算をあらわすことに注意。

##実装

k = 2
m, n = 3, 5
iters = 30

M = np.random.randint(1, 6, (m, n))

U = np.abs(np.random.uniform(low=0, high=1, size=(m, k)))
V = np.abs(np.random.uniform(low=0, high=1, size=(n, k)))

for _ in range(iters):
    U, V = update_uv(M, U, V)

X = np.dot(U, V.T)

# M =
# [[1 4 1 5 4]
#  [5 3 3 1 3]
#  [2 4 2 5 4]]

# X =
# [[ 0.97226794  3.8740713   1.19828474  5.14962285  3.8740713 ]
#  [ 4.9954159   2.96768054  3.05263671  1.04196113  2.96768054]
#  [ 2.02462211  4.14097417  1.77570319  4.83147475  4.14097417]]

コスト関数

$||M - UV^T||_F^2$は以下のように推移する。

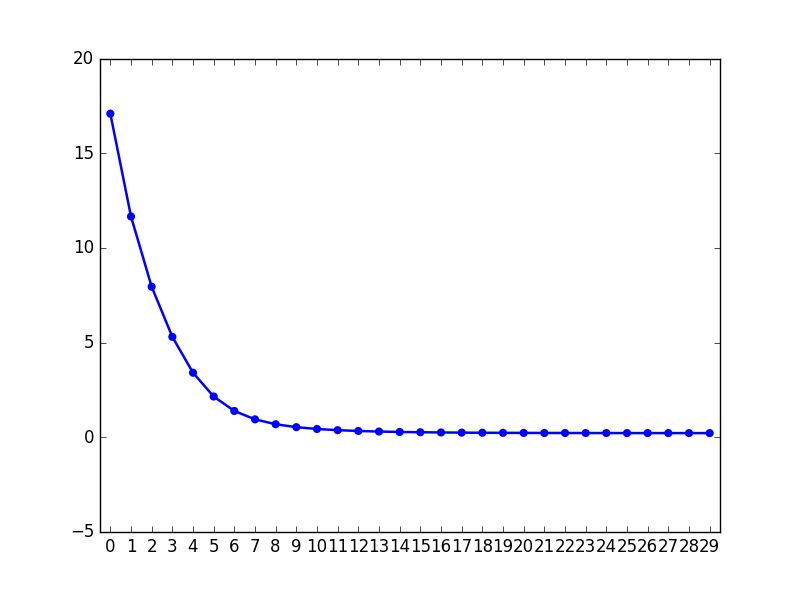
なお……

scikit-learnにはNMFが実装されているので結果だけが必要ならこちらを使えばよい。
http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.NMF.html