CTFにおけるLLLの使い方を現役エンジニアが解説

仕事でLLLは使っていないです。

LLL（Lenstra–Lenstra–Lovász lattice basis reduction algorithm、Lenstra–Lenstra–Lovász格子基底簡約アルゴリズム）は、CTFのCryptoジャンルで、RSAや楕円曲線の次くらいの中難易度の問題に出てくる。昨年末に開催されたSECCON CTF 2021では、Cryptoの6問中3問がLLLを使う問題だった。SECCON CTF 2021の作問に関わり、テスターとしてLLLを使う問題を解いたりレビューのやりとりを眺めていたりして、だいぶLLLが理解できたので、それらの問題の解説と合わせてまとめておく。

LLL

Lenstra–Lenstra–Lovász lattice basis reduction algorithm - Wikipedia

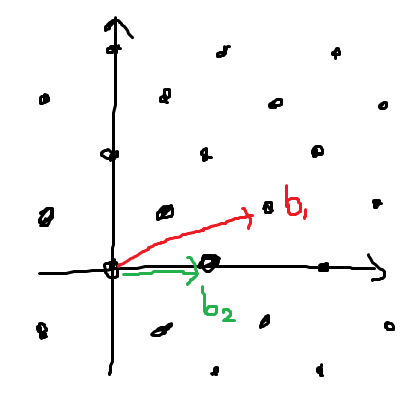
ベクトルの集合 $\mathbf{B} = \{\mathbf{b}_1, \mathbf{b}_2, \dots, \mathbf{b}_n\}$ が与えられたとき、

（数式の表示がバグるので改行）これらのベクトルの整数係数線形結合で得られる点の集合 $\Lambda = \mathcal{L}(B) = \{\sum_{i=1}^n a_i \mathbf{b}_i | a_i \in \mathbb{Z}\}$ を「格子」という。このとき、$\mathbf{B}$ を $\Lambda$ の「基底」という。例えば、基底 $\mathbf{b}_1 = (3, 1)$, $\mathbf{b}_2 = (2, 0)$ が作る格子 $\Lambda$ には次のような点が含まれる。

\begin{eqnarray}
(0, 0) &=& 0\times\mathbf{b}_1+0\times\mathbf{b}_2, \\
(3, 1) &=& 1\times\mathbf{b}_1+0\times\mathbf{b}_2, \\
(1, 1) &=& 1\times\mathbf{b}_1-1\times\mathbf{b}_2, \\
(-11, -7) &=& -7\times\mathbf{b}_1+5\times\mathbf{b}_2 \\
\end{eqnarray}

図示してみると「格子」っぽさを感じる。

CTFの問題だとベクトルの個数も要素数も数百くらいまでの問題を良く見る。LLLの計算量のオーダーを見ると無理そうだけれど、オーダーは最悪ケースであって、たぶん、たいていの場合はもっと早く終わるのだろう。ベクトルの要素は有理数や実数であっても良い。剰余類環（mod nで計算するやつ）はたぶんダメ。

同じ格子を作る基底は複数ある。上記の例では、$\mathbf{b}'_1 = (1, 1)$, $\mathbf{b}'_2 = (1, -1)$ でも同じ格子になる。

\begin{eqnarray}
(0, 0) &=& 0\times\mathbf{b}'_1+0\times\mathbf{b}'_2, \\
(3, 1) &=& 2\times\mathbf{b}'_1-1\times\mathbf{b}'_2, \\
(1, 1) &=& 1\times\mathbf{b}'_1+0\times\mathbf{b}'_2, \\
(-11, -7) &=& -9\times\mathbf{b}'_1-2\times\mathbf{b}'_2 \\
\end{eqnarray}

LLLは、ベクトルの集合を入力として、その集合と同じ格子を作る、短いベクトルの集合を求めるアルゴリズムである。もっとも、最短のベクトルを求めるのは難く、LLLは近似的な解を返す。

近似率がどのくらいかは、上述のWikipediaに書かれている。LLLの定義のものではなく、「Properties of LLL-reduced basis」のほうが使うはず。まあ、論文を書くとかで「どのくらいまでなら解けるか？」を解析するなら必要だろうけど、CTFの問題で出てくるということは解ける問題設定になっているはずで、あまり気にする必要は無いと思う。

SageMath

実際に使うには、SageMathの Matrix に実装されている LLL メソッドが簡単。

SageMathのインストール方法は色々と用意されている。Dockerを使うのが楽だろうか。ちょっと計算するだけならインタラクティブシェルでも良いけれど、普通はスクリプトを書いて実行することになるはず。

test.sage

M1 = Matrix([
  [3, 1],
  [2, 0],
])

M2 = M1.LLL()

print(M2)

>docker run --rm -it -v %CD%:/host sagemath/sagemath sage /host/test.sage
[-1 -1]
[ 1 -1]

Windows。Linuxなら %CD% の代わりに $(pwd)。

格子のベクトルの集合は、各ベクトルを行にした行列で表わすことが多い。ここで注意があって、ベクトルを行にするのか列にするのかが統一されていない。解説を読むときには、どちらなのかを気にしないといけない。

LLLの使い方

この辺までは分かっていて、「で、同じ格子を表わす別のベクトルの集合を見つけてどうするの？」ということが分かっていなかった。

ほとんどの問題では、ベクトルの集合は必要としない。必要なのは集合の中の短い1個のベクトルである。LLLの出力する集合の中の個々のベクトル自身も格子に含まれる。つまり、入力のベクトルの整数係数線形結合になっている。それはそうで、あるベクトル $\mathbf{b}_i$ の係数を1、他のベクトルの係数を0とすれば、 $\mathbf{b}_i$ になるから。入力のベクトルの整数係数線形結合であって、ノルムの小さいベクトルを求めるための道具として、LLLを使う。格子の中で原点に最も近い点を求める問題をShortest vector problem（SVP）と言う。これを厳密に求めるのはNP困難。

作る格子の基本形はこんな感じ。

\begin{pmatrix}
1 & 0 & 0 & \cdots & ? & ? \\
0 & 1 & 0 & \cdots & ? & ? \\
0 & 0 & 1 & \cdots & ? & ? \\
\vdots & \vdots & \vdots & & \vdots & \vdots \\
\end{pmatrix}

求めたい変数を各行に対応させる。これをLLLに投げると、LLLは、各変数に $?$ の部分の係数を掛けて足し合わせときに小さくなる解を見つけてくれる。そのときの変数の値は、ベクトルの左側の部分の値を見れば分かる。変数が1回足されれば、ベクトルの要素の値も1増えるため。

例えば、

8053 x + 343 y + 1362 z

の絶対値を小さくするような、全てが0ではない $x$, $y$, $z$ の値を求めたいときは、

\begin{pmatrix}
1 & 0 & 0 & 8053 \\
0 & 1 & 0 & 343 \\
0 & 0 & 1 & 1362 \\
\end{pmatrix}

をLLLに投げれば良い。実際に投げたら、次の答えが返ってきた。

\begin{pmatrix}
0 & -4 & 1 & -10 \\
-3 & -5 & 19 & 4 \\
-2 & 35 & 3 & -15 \\
\end{pmatrix}

例えば2行目は、$x=-3$, $y=-5$, $z=19$ という解に対応している。

8053 \times (-3) + 343 \times (-5) + 1362 \times 19 = 4

ナップサック暗号（部分和問題）

LLLと言えばこの問題。

整数の集合 $A$ と整数 $X$ が与えられ、 $A$ の部分集合 $B \subset A$ で合計が $X$ となるものを答える。上記の基本形ほぼそのままで解ける。

例えば、 $A = \{50, 137, 38, 197, 120, 206\}$ と $X = 295$ だと、

\begin{pmatrix}
1 & 0 & 0 & 0 & 0 & 0 & -50 \\
0 & 1 & 0 & 0 & 0 & 0 & -137 \\
0 & 0 & 1 & 0 & 0 & 0 & -38 \\
0 & 0 & 0 & 1 & 0 & 0 & -197 \\
0 & 0 & 0 & 0 & 1 & 0 & -120 \\
0 & 0 & 0 & 0 & 0 & 1 & -206 \\
0 & 0 & 0 & 0 & 0 & 0 & 295 \\
\end{pmatrix}

をLLLに投げる。結果は次のようになった。

\begin{pmatrix}
 0 &  1 &  1 &  0 &  1 &  0 &  0 \\
 1 &  0 &  1 &  0 &  0 &  1 &  1 \\
-1 & -1 &  0 & -1 &  0 & -1 &  0 \\
 0 & -1 &  1 &  2 &  0 &  0 &  0 \\
 1 & -1 &  0 &  0 &  0 & -1 & -2 \\
-1 & -2 &  0 &  0 &  1 &  1 & -2 \\
-1 &  1 &  2 &  1 & -3 &  0 &  0 \\
\end{pmatrix}

LLLでは出力の行の並びにも意味があって、小さいものが上のほうの行に出てくる。右端が0で、それ以外が0か1だけの行が出てくれば成功である。$A$ の部分集合と $X$ で0が作れたということだから。1行目が答えで、 $137+38+120=295$。この手法が書かれている論文の著者名から、LO法と呼ばれている¹。

もし、条件を満たす行が出てこなかったら、$A$ の要素数を $n$ として、右端の列の各要素に $\sqrt{n}$ より大きな値（$n$ とか）を掛ければ良い。LLLの結果の行列にもその値が掛けられることになり、0はそのままだけれど、それ以外の値が大きくなる。LLLは右端の値を非ゼロにすることよりも、それ以外の列の値を1にすることを選択するようになる。

それでもダメなら、 $X$ を $X'=\sum{A}-X$ に置き換える。置き換えた問題の答えは、 $A$ の要素を選ぶ／選ばないが反転したものとなる。そうすると行列の0と1も反転し、もし答えに1が多い場合、0と1が反転することでベクトルが小さくなり、LLLの結果として出てきやすくなる。

「ところで、ナップサック問題ってNP困難じゃなかったっけ？」というのが気になってくる。実際、この方法で解けるのは、ナップサック問題の「密度」が低い場合だけである。密度とは、入力の要素数を $n$、要素のビット幅を $b$ として、$\frac{n}{b}$。LO法はこの値が0.645...未満の問題が解ける。

正確には、0.645...未満の「ほとんど全て」（almost all）の問題が解けると言っている。解けない問題もある。それはそうで、全ての問題が解けるなら、密度が高い問題でも要素に適当な同じ定数を足してビット数を増やすことで解けてしまう。この密度は、要素が乱数であると仮定して、 $n \to \infty$ の極限を取った値っぽい。非ゼロ最短ベクトルが、求める答えとならない確率を計算している。密度が高いと、1と-1の両方を含んでいたり、1の代わりに2を含んでいたりするベクトルが出てくる確率が高まるのだろう。

LO法の改良で、CLOS法というものがある²。行列をこう書き換えるだけ。

\begin{pmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 50 N \\
0 & 1 & 0 & 0 & 0 & 0 & 137 N \\
0 & 0 & 1 & 0 & 0 & 0 & 38 N \\
0 & 0 & 0 & 1 & 0 & 0 & 197 N \\
0 & 0 & 0 & 0 & 1 & 0 & 120 N \\
0 & 0 & 0 & 0 & 0 & 1 & 206 N \\
\frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & 295 N \\
\end{pmatrix}

$N=1$としたときの出力は、

\begin{pmatrix}
 \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} &  \frac{1}{2} & -\frac{1}{2} &  \frac{1}{2} &    0 \\
 \frac{1}{2} & -\frac{1}{2} &  \frac{1}{2} &  \frac{1}{2} &  \frac{1}{2} &  \frac{1}{2} &    0 \\
 \frac{1}{2} & -\frac{1}{2} &  \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} &  \frac{1}{2} &   -1 \\
 \frac{3}{2} & -\frac{1}{2} &  \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} &    1 \\
  -1 &   -1 &    0 &    1 &   -1 &   -1 &    0 \\
  -1 &   -2 &    0 &   -1 &    0 &    1 &    1 \\
   0 &    2 &    2 &    1 &   -1 &    1 &    1 \\
\end{pmatrix}

$N$ は $\sqrt{n}$ 程度の定数。論文に合わせて書いたが、右端以外の値を2倍して整数で扱うことが多いと思う。最後の行に $\frac{1}{2}$ があることが重要。（符合を変えたことと）これで、出力が0か1から、$\pm\frac{1}{2}$になる。答えのベクトルが小さくなるから、答えではないベクトルがLLLの出力になることが防げるらしい。これで、密度0.9408...まで解ける。密度が1以上だとナップサック問題の解が複数になってきて使えないことと合わせて考えると、ナップサック問題ベースの暗号で使われているものが無いのも頷ける。

oOoOoO

problem.py

import signal
from Crypto.Util.number import long_to_bytes, bytes_to_long, getPrime
import random
from flag import flag

message = b""
for _ in range(128):
    message += b"o" if random.getrandbits(1) == 1 else b"O"

M = getPrime(len(message) * 5)
S = bytes_to_long(message) % M

print("M =", M)
print('S =', S)
print('MESSAGE =', message.upper().decode("utf-8"))

signal.alarm(600)
ans = input('message =').strip().encode()

if ans == message:
    print(flag)
else:
    print("🧙")

サーバーは、oとOだけで構成される128文字のランダムな文字列messageと、640ビットのランダムな素数Mを生成する。MとS = bytes_to_long(message)%Mだけからmessageを当てられたら、フラグが出てくる。

oとOで文字コードが0x20違うことに気が付けば解ける。SからOOO...Oを引くと、0x20, 0x2000, 0x200000, ...から数字を選んで足し合わせるナップサック問題になる。ただし、mod M。「Mの足し引きは自由にしてくれ」という気持ちで、行列に1行付け足せば良い。こんな行列を作る。

\begin{pmatrix}
2 & 0 & 0 & \dots & 32 \cdot 256^0 n \\
0 & 2 & 0 & \dots & 32 \cdot 256^1 n \\
0 & 0 & 2 & \dots & 32 \cdot 256^2 n \\
\vdots & \vdots & \vdots & & \vdots \\
1 & 1 & 1 & \dots & Sn \\
0 & 0 & 0 & \dots & Mn \\
\end{pmatrix}

この行列は行数が列数よりも多いので、1次従属（余計な行がある）である。「格子暗号解読のための数学的基礎」によると、こういう行列を扱うときはLLLに一工夫必要らしいが、SageMathのLLLは対応しているようで、1行目に0だけのベクトルが出てくる。答えは2行目になる。

なお、作問者解答は、「modと言ったって128通りしかないのだから、普通のナップサック暗号の解法を128通り試せば良いでしょ？」というもの。なるほど。

solve.sage

M = int(input("M = "))
S = int(input("S = "))

n = 128
S -= int.from_bytes(b"O"*n, "big")

X = [[0]*(n+1) for _ in range(n+2)]
for i in range(n):
  X[i][i] = 2
  X[i][n] = 0x20*256**i*n
for i in range(n):
  X[n][i] = 1
X[n][n] = S*n
X[n+1][n] = M*n

X = Matrix(X).LLL()

ans = X[1]
assert ans[-1]==0
ans = ans[:-1]
assert all(a in (-1, 1) for a in ans)

ans = "".join("O" if a==1 else "o" for a in ans)[::-1]
print(ans)

XXX

task.sage

import os

flag = os.getenv("FLAG", "fake{fakeflag_blahblah}")
x = int.from_bytes(flag.encode(), "big")

p = random_prime(1 << int(x.bit_length() * 2.5))
Fp = GF(p)

params = []
while len(params) != 6:
    try:
        y = randint(2, x)
        a = randint(2, p-1)
        b = (y^2 - (x^3 + a*x)) % p

        EC = EllipticCurve(Fp, [a, b])
        EC(x, y)

        params.append([a, b])
    except ValueError:
        pass

print(p)
print(params)

楕円曲線である……ことはあまり気にしなくて良くて、次の連立方程式の $a_i$ と $b_i$ が与えられて、$x$ を求める問題と思えば良い。

\begin{eqnarray*}
y_0^2 &\equiv& x^3 + a_0 x + b_0 \mod p \\
y_1^2 &\equiv& x^3 + a_1 x + b_1 \mod p \\
y_2^2 &\equiv& x^3 + a_2 x + b_2 \mod p \\
 &\vdots& \\
\end{eqnarray*}

$x^3$ は $p$ より大きくて邪魔なので、両辺を引いて消す。$a_i' = a_{i+1}-a_i$、$b_i' = b_{i+1}-b_i$ として、

\begin{eqnarray*}
y_1^2 - y_0^2 &\equiv& a_0' x + b_0' \mod p \\
y_2^2 - y_1^2 &\equiv& a_1' x + b_1' \mod p \\
y_3^2 - y_2^2 &\equiv& a_2' x + b_2' \mod p \\
 &\vdots& \\
\end{eqnarray*}

$p$ が $x^{2.5}$ 程度であるところ、$y_{i+1}^2-y_i^2$ は $x^2$ くらい。$a_i'x+b_i' \mod p$ を全て小さくする $x$ を求める問題になる。

この行列を入力にする。

\begin{pmatrix}
2^{320} & 0 & a_0' & a_1' & a_2' \\
0 & 2^{1024} & b_0' & b_1' & b_2' \\
0 & 0 & p & 0 & 0 \\
0 & 0 & 0 & p & 0 \\
0 & 0 & 0 & 0 & p \\
\end{pmatrix}

$2^{1024}$ は、LLLに「$b_i'$ はなるべく使うな」と圧を掛けるため。大きければ何でも良い。こうすると、LLLはまずは $b_i'$ を使わないベクトルを出してきて、とはいえ同じ格子を生成できないといけないので全く使わないわけにもいかず、1回だけ使った（2列目が $\pm 2^{1024}$ の）ベクトルを最後に出してくる。

$2^{320}$ は、予想できる $x$ のビット数。これによって1列目の値を $y_{i+1}^2-y_i^2 \simeq x^2$ に揃える。LLLは、これが小さいと3列目以降を（1列目の値を大きくしてでも）無理に小さくしようとするし、大きいと1列目を無理に小さくしてしまう。

$x$ の値をランダムに決めると、 $a_i'x+b_i' \mod p$ の値は $p \simeq x^{2.5}$ 未満のランダムな値になると考えられ、それが $x^2$ 以下になるのは $\frac{1}{x^{0.5}}$ 程度の確率なので、使う式は3個で充分。

solve.sage

p = 238351830708404244219528012300346183698089704036958197073088590986781126046128139277876261847918986388464392075919752504036124478387675086320279831883061575773130731731512289308600548817918823754759741014480607490178191084213685771095081699
params = [[61721446814822499191022412902217320153137633897387846710512310039336410477728264217681745891863200893378034581997664894522756658992873501693353425063400655105194107970249009691442632015429658305792298714043235777934090212343625933540920419, 38215859743437160276358618194105173963536621422404142018824002222927344371846641995139103441786202367296704680389815780441043250270096100089370169391316241550354639472704197195039115443263083720157181161573037786722518518073244876576521645], [193846031065431615171138398907554474490243593010426445660159995023421690918389029501570918601414789147460375901577546434319012002193067152560178159337882412597981169953017381602553449608161376011387225337945790490301205500988070592667260307, 182624605832152240064165962388331595893516884552600324435147374044032575325900262356701606616541732441503871912325334315545721127713601115727804588364391211951651086408749934094159068720206922998283686393892033283362379079277585875317733125], [186116431294956584507622251083552464237708766317037184701883695099192545170797758914491959325056548294443112027689221562090922906211642613451222485059412249593287539268632182815867453113262026976033832305075048778306269837158521655897206104, 188291640755725711120730552161550568363878329035151394705358843149734090074525252662747799270008290175006002913694732659518178709233238519205580102532883270488509830279127451754878651121923932212399426641171488518541036604555898762653636767], [147690737704193380929256042516354642591634312528093128869923487184997632263182669491324548799394778507341925228715095053166787082158079876801508640863174460376667578857398193776134734184654976792585753897823602173550210678811026343180632574, 90919616852165947744756990575400745193091744707583913218090901120971522401412921713920030755420236486444344985420141669115268509030823280811858196495296299291522098961629224878356500400137160049480897176934761512803911650692781199738944358], [147919066213305504909474311411803269104114976277480371373734903513860210330631554119249090143860674441819199276919740940095535099825251133312941478015230935296046855247122689436697731644543102898280018067875178726421332069314230553359546674, 233189046301154960459915044289449599538936202863814191691219472024725663885482828960872087873090796952667099967198895490748125927000604303160065032535117589864975437392352615652017307656160862671237257143553966268386859872891179982158931538], [137450316462129268877711035250763668980618551403674476273480945205694245899369623646082468202341690739837762419221648759226283935459299779254296497766202256170266366890970940886869389464332464546003480305741255956702385666111816886488497002, 42626852637723346847761898432034196330200006970228231831316278507491404141071325164359383210554480496801017672657717855189744860778897395023272448045289999028710960807199386287807443723368642574520040320693565244086076826717435666078357317]]

a, b = zip(*params)

a = [(a[i+1]-a[i])%p for i in range(len(a)-1)]
b = [(b[i+1]-b[i])%p for i in range(len(b)-1)]

M = [
  [2^320, 0,      a[0], a[1], a[2]],
  [0,     2^1024, b[0], b[1], b[2]],
  [0,     0,      p,    0,    0],
  [0,     0,      0,    p,    0],
  [0,     0,      0,    0,    p],
]

M = Matrix(M).LLL()

x = abs(M[-1][0])
print(int(x).to_bytes(128, "big").decode().strip("\0"))

Sign_Wars（前半）

後半は乱数推測と楕円曲線暗号なので、LLLである前半だけ。

challenge.sage

from Crypto.Util.number import bytes_to_long, long_to_bytes
from Crypto.Util.Padding import pad
import random
from secret import msg1, msg2, flag

flag = pad(flag, 96)
flag1 = flag[:48]
flag2 = flag[48:]

# P-384 Curve
p = 39402006196394479212279040100143613805079739270465446667948293404245721771496870329047266088258938001861606973112319
a = -3
b = 27580193559959705877849011840389048093056905856361568521428707301988689241309860865136260764883745107765439761230575
curve = EllipticCurve(GF(p), [a, b])
order = 39402006196394479212279040100143613805079739270465446667946905279627659399113263569398956308152294913554433653942643
Z_n = GF(order)
gx = 26247035095799689268623156744566981891852923491109213387815615900925518854738050089022388053975719786650872476732087
gy = 8325710961489029985546751289520108179287853048861315594709205902480503199884419224438643760392947333078086511627871
G = curve(gx, gy)

for b in msg1:
    assert b >= 0x20 and b <= 0x7f
z1 = bytes_to_long(msg1)
assert z1 < 2^128

 :

# prequel trilogy
def sign_prequel():
    d = bytes_to_long(flag1)
    sigs = []
    for _ in range(80):
        # normal ECDSA. all bits of k are unknown.
        k1 = random.getrandbits(128)
        k2 = z1
        k3 = random.getrandbits(128)
        k = (k3 << 256) + (k2 << 128) + k1
        kG = k*G
        r, _ = kG.xy()
        r = Z_n(r)
        k = Z_n(k)
        s = (z1 + r*d) / k
        sigs.append((r,s))

    return sigs
 :

楕円曲線DSA。この問題も（前半は）楕円曲線のことは考えなくて良い。$r_i$ と $s_i$ が与えられ、下の式を満たす384ビットの $d$ と128ビットの $z$, $x_i$, $y_i$ を求める。数式が書きづらいので、コード中の k1, k2 = z1, k3, order をそれぞれ $x_i$, $z$, $y_i$, $p$ にしている。$z$ と $d$ が分かれば、$x_i$ と $y_i$ は求められる。

s_i \equiv \frac{z+r_i d}{2^{256}y_i+2^{128}z+x_i} \mod p\ \ (0\leq i <80)

変形して、

- r_i d + \left(2^{128} s_i - 1\right) z + s_i x_i + 2^{256} s_i y_i \equiv 0 \mod p\ \ (0\leq i <80)

結局、連立方程式を成り立たせる、小さな解を求めよという問題に落ちる。

作る行列はこう。

\begin{pmatrix}
1 & 0 & 0 & 0 & \cdots & 0 & 0 & \cdots & -r_0 & -r_1 & \cdots \\
0 & 2^{256} & 0 & 0 & \cdots & 0 & 0 & \cdots & 2^{128}s_0-1 & 2^{128}s_1-1 & \cdots \\
0 & 0 & 2^{256} & 0 & \cdots & 0 & 0 & \cdots & s_0 & 0 & \cdots \\
0 & 0 & 0 & 2^{256} & \cdots & 0 & 0 & \cdots & 0 & s_1 & \cdots \\
\vdots & \vdots & \vdots & \vdots & & \vdots & \vdots & & \vdots & \vdots & \\
0 & 0 & 0 & 0 & \cdots & 2^{256} & 0 & \cdots & 2^{256}s_0 & 0 & \cdots \\
0 & 0 & 0 & 0 & \cdots & 0 & 2^{256} & \cdots & 0 & 2^{256}s_1 & \cdots \\
\vdots & \vdots & \vdots & \vdots & & \vdots & \vdots & & \vdots & \vdots & \\
0 & 0 & 0 & 0 & \cdots & 0 & 0 & \cdots & p & 0 & \cdots \\
0 & 0 & 0 & 0 & \cdots & 0 & 0 & \cdots & 0 & p & \cdots \\
\vdots & \vdots & \vdots & \vdots & & \vdots & \vdots & & \vdots & \vdots & \\
\end{pmatrix}

各行はそれぞれ $d$, $z$, $x_0$, $x_1$, …, $y_0$, $y_1$, …に対応している。ごちゃごちゃするので省略したけど、右側の列の各値には $2^{1024}$ 程度の大きな値を掛けて、式の右辺がちゃんと0になるようにする。左側の列が1列目以外 $2^{256}$ になっているのは、 $d$ が384ビットで、他が128ビットなのを揃えるため。 $384-128=256$。

この連立方程式には、 $d=p$, $z=x_i=y_i=0$ という解がある。この解に対応するベクトルは充分小さくて、まずこれが出てくるので、2行目を出力している。式が80個あるのはこの後の乱数推測に使うためで、ここではそんなに必要無い。計算が重くなるので一部だけを使う。

solve.sage

import random

sigs1, sigs2 = map(eval, open("output.txt").read().split("\n")[:2])

order = 39402006196394479212279040100143613805079739270465446667946905279627659399113263569398956308152294913554433653942643

n = 8 #len(sigs1)

M = [[0]*(2+3*n) for _ in range(2+3*n)]
M[0][0] = 1
for i in range(1, 2+2*n):
  M[i][i] = 2^256
for i in range(n):
  r, s = sigs1[i]
  M[0    ][2+2*n+i] = -r
  M[1    ][2+2*n+i] = (2^128*s-1)
  M[2+i  ][2+2*n+i] = s
  M[2+n+i][2+2*n+i] = 2^256*s
for i in range(n):
  M[2+2*n+i][2+2*n+i] = order
for i in range(2+3*n):
  for j in range(2+2*n, 2+3*n):
    M[i][j] *= 2^1024

M = Matrix(M).LLL()

flag1 = abs(M[1][0])
z1 = abs(M[1][1])

print("flag1:", int(flag1).to_bytes(64, "big").decode().strip("\0"))
print("z1:", int(z1).to_bytes(64, "big").decode().strip("\0"))

1. LAGARIAS, Jeffrey C.; ODLYZKO, Andrew M. Solving low-density subset sum problems. Journal of the ACM (JACM), 1985, 32.1: 229-246. ↩

2. COSTER, Matthijs J., et al. An improved low-density subset sum algorithm. In: Workshop on the Theory and Application of of Cryptographic Techniques. Springer, Berlin, Heidelberg, 1991. p. 54-67. ↩