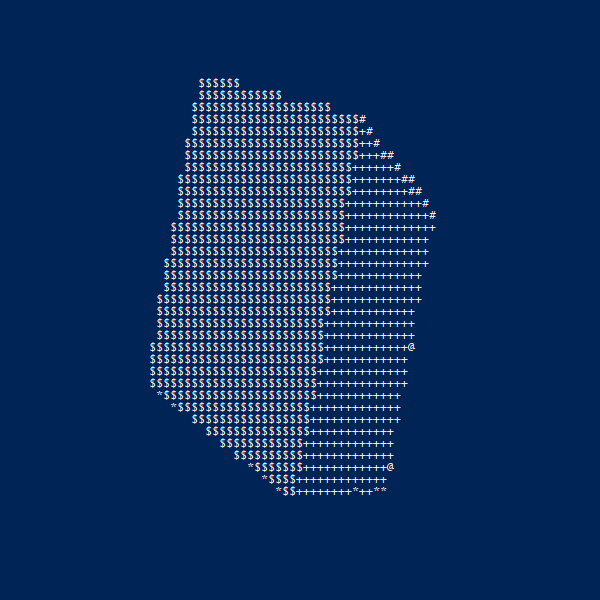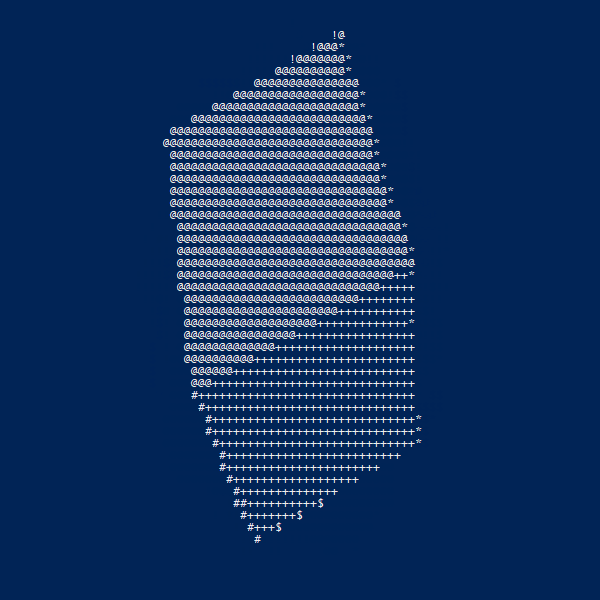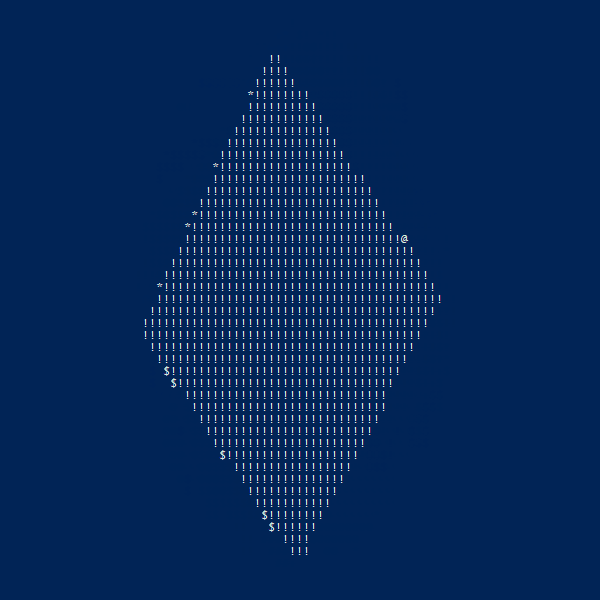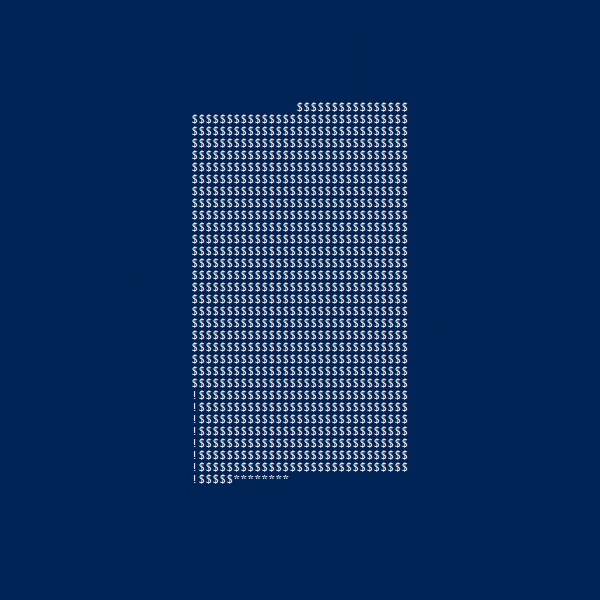はじめに
回れ!ドーナッツ!
概要
Donut math: how donut.c worksを参考に、ターミナル上でドーナツを回すコードを、Pythonを使って書いてみました。
今回はこのコードの仕組みをブレークダウンして解説します。
(コンピュータグラフィックの基礎や、プログラミングにおける数学の大切さがわかるかもしれません。)
コードはこちら
import math
import time
window_width = 100
window_height = 100
K2 = 5
div1 = 50
div2 = 50
R1 = 1
R2 = 2
K1 = window_width*K2*3/(8*(R1+R2))
characters = ".,-~:;=!*#$@"
def calc_surface(A, B):
# よく使う変数をあらかじめ計算
sinA = math.sin(A)
sinB = math.sin(B)
cosA = math.cos(A)
cosB = math.cos(B)
# ターミナル上に投影する文字を格納する配列
display = [[" " for i in range(window_width)]for j in range(window_height)]
# z_bufferを管理するための配列
z_buffer = [[0 for i in range(window_width)] for j in range(window_height)]
# ターミナル上に投影する文字を格納する配列
for theta in [(2*math.pi*x)/div1 for x in range(div1)]:
for phi in [(2*math.pi*x)/div2 for x in range(div2)]:
# よく使う変数をあらかじめ計算その2
cosphi = math.cos(phi)
costheta = math.cos(theta)
sinphi = math.sin(phi)
sintheta = math.sin(theta)
circlex = R2+R1*costheta
circley = R1*sintheta
# ドーナツの表面上の点を計算
x = (circlex)*(cosB*cosphi+sinA*sinB*sinphi)-circley*cosA*sinB
y = (circlex)*(cosphi*sinB-cosB*sinA*sinphi)+circley*cosA*cosB
z = K2 + (cosA*circlex*sinphi + circley*sinA)
# ドーナツをターミナル上に投影した時の位置を計算
display_x = int(window_width/2 + (K1 * x) / (K2 + z))
display_y = int(window_height/2 - (K1 * y) / (K2 + z))
# zバッファーの計算
if z_buffer[display_y][display_x] < 1/z:
z_buffer[display_y][display_x] = 1/z
# 光の反射を計算
L = cosphi*costheta*sinB - cosA*costheta*sinphi - sinA * \
sintheta + cosB*(cosA*sintheta - costheta*sinA*sinphi)
# 計算された光の反射をもとに文字に変換する
display[display_y][display_x] = characters[int(L*8)]
return "\n".join(["".join(line) for line in display])
# ターミナル上でアニメーションを表現するための下準備
# あらかじめ表示する行数だけカーソルを下に移動させる
print(f"\033[{window_height}S", end="")
# 最初の行へ戻す
print(f"\033[{window_height}A", end="")
# 最初の行の位置を記憶しておく
print("\033[s", end="")
A = 0
B = 0
while True:
A += 0.15
B += 0.1
img = calc_surface(A, B)
# 記憶された情報をもとに最初の行の位置へ移動する
print("\033[u", end="")
print(img, flush=True)
time.sleep(0.05)
ドーナツ描画の仕組み
描画の大まかな流れ
ドーナツの描画は、「ドーナツの表面の点の座標を計算し」「それらの点をターミナル上に投影する」という流れで行われています。
まず最初に、ドーナツの表面上の点を計算する方法を見ていきましょう。
ドーナツの表面の各点の座標の計算
静止しているドーナツの表面の各点を求める
最初に静止しているドーナツの表面の点の座標を求めていきます。(回すのは後回しです。)
立体上のドーナツの各点の座標は、平面上の円を回転させた、回転体として表現することができます。
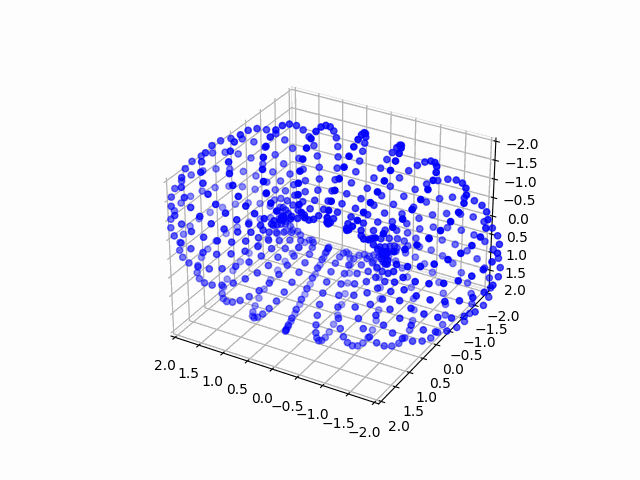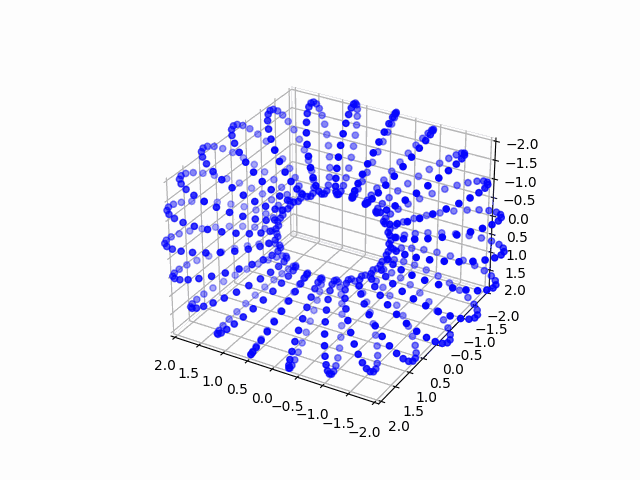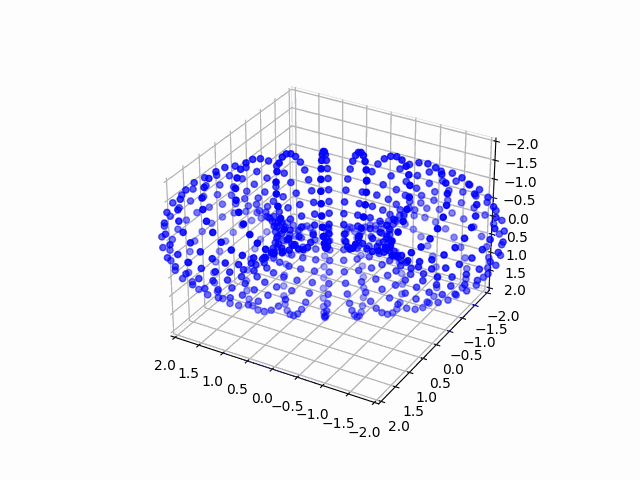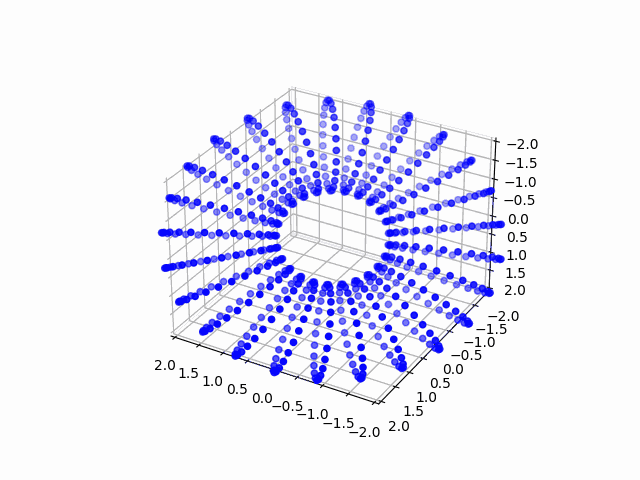
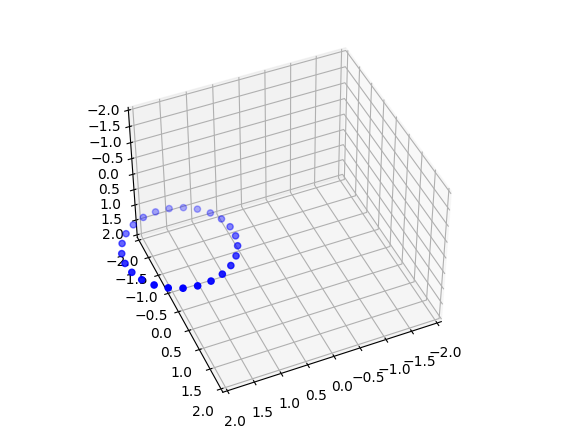
まず、平面上の円の座標は、円の半径を$R_1$とすると、以下の数式で表すことができます。(今後、回転させることを考えて、x方向に$R_2$だけずらしておきます)
\begin{bmatrix}
x&y&z
\end{bmatrix}
=
\begin{bmatrix}
R_2 + R_1\cos \theta & R_1\sin \theta &0
\end{bmatrix}
図で表すと以下のようになります。(適当な単位で$\theta$を区切って座標を求め、matplotlibで表示しました。)
次はこれをy方向を軸として回転させ、回転体を作っていきます。
y方向を軸とした回転後の座標は、回転行列を用いて以下のように計算できます
\begin{align}
\begin{bmatrix}
x&y&z
\end{bmatrix}
& =
\begin{bmatrix}
R_2 + R_1\cos \theta & R_1\sin \theta &0
\end{bmatrix}
\begin{bmatrix}
\cos \phi & 0 & \sin \theta \\
0 & 1 & 0 \\
-\sin \phi & 0 & \cos \phi
\end{bmatrix} \\
& =
\begin{bmatrix}
(R_2+ R_1\cos \theta)\cos \phi & R_1\sin \theta & -(R_2+R_1\cos\theta)\sin \phi
\end{bmatrix}
\end{align}
図で表すと以下のようになります。(適当な単位で$\phi$を区切って座標を求めています)
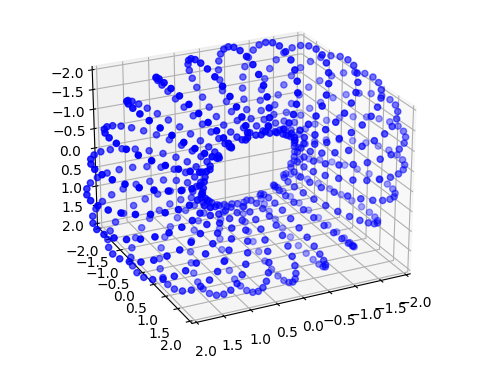
ドーナツが表現できました。
ドーナツを回す
さて、ドーナツの表面上の点の座標が求まったところで次にドーナツを回していきましょう。
先ほどは円をy軸を中心に回転させることによって、ドーナツを作成しました。そのため、y軸方向にいくら回転させても、ドーナツ自体を動かすことはできません。
よって、x軸とz軸を中心に回転させていきます。
x軸を中心とした回転量を$A$, z軸を中心とした回転量を$B$とし、先ほどのy軸を中心とした回転と合わせて座標を計算すると以下のようになります。(長いので計算結果は割愛)
\begin{bmatrix}
x&y&z
\end{bmatrix}
=
\begin{bmatrix}
R_2 + R_1\cos \theta & R_1\sin \theta &0
\end{bmatrix}
\begin{bmatrix}
\cos \phi & 0 & \sin \theta \\
0 & 1 & 0 \\
-\sin \phi & 0 & \cos \phi
\end{bmatrix} \\
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos A & \sin A \\
0 & -\sin A & \cos A
\end{bmatrix} \\
\begin{bmatrix}
\cos B & \sin B & 0 \\
-\sin B & \cos B & 0 \\
0 & 0 & 1
\end{bmatrix} \\
これを、$\theta$と$\phi$を$0$から$2\pi$の範囲で適当に区切り、$A$と$B$を変更しながら描写すると・・・
ドーナツを回すことができるようになりました!
matplotlib上でドーナツを回すコードはこちら
import math
import matplotlib.pyplot as plt
import matplotlib.animation as animation
fig = plt.figure()
div1 = 25
div2 = 25
R1 = 1
R2 = 2
def make_points(A,B):
x = []
y = []
z = []
sinA = math.sin(A)
sinB = math.sin(B)
cosA = math.cos(A)
cosB = math.cos(B)
for theta in [(2*math.pi*x)/div1 for x in range(div1)]:
for phi in [(2*math.pi*x)/div2 for x in range(div2)]:
cosphi = math.cos(phi)
circlex = R2+R1*math.cos(theta)
circley = R1*math.sin(theta)
cordx = (circlex)*(cosB*cosphi+sinA*sinB*math.sin(phi))-circley*cosA*sinB
cordy = (circlex)*(cosphi*sinB-cosB*sinA*math.sin(phi))+circley*cosA*cosB
cordz = (cosA*(circlex)*math.sin(phi) + circley*sinA)
x.append(cordx)
y.append(cordy)
z.append(cordz)
return x,y,z
ax = fig.add_subplot(projection='3d')
A = 0
B = 0
def plot(data):
print(data)
ax.cla()
ax.set_xlim(2,-2)
ax.set_ylim(2,-2)
ax.set_zlim(2,-2)
global A
global B
A += 0.1
B += 0.1
x,y,z = make_points(A,B)
ax.scatter(x, y, z, color='blue')
ani = animation.FuncAnimation(fig, plot, interval=100, frames=100)
ani.save("test.gif", writer="imagemagick")
plt.show()
ターミナル上に投影する文字の計算
ドーナツの表面上の点の座標が計算できたため、次はこれをターミナル上に投影することを考えます。
ターミナル上に投影する文字は、「各点が投影されるべき位置がどこになるかを計算」し、「どの点を描画するべきか判断」したのちに、「どの文字で表現するべきかを計算する」ことで求めることができます。
投影位置の計算
まず、ドーナツの表面上の各点がターミナル上ではどの位置に当たるか?を計算します。
例えば、視点から距離$z$の位置にある物体を距離$z'$の位置にあるスクリーンに投影することを考えると、その物体のスクリーン上の大きさは$\frac{z'}{z}$となります。
よって、各点をスクリーン上に投影した場合の座標$(x', y')$は以下のように求まります。
x'=\frac{xz'}{z}, y'=\frac{yz'}{z}
この時、目の位置からスクリーンまでの位置を$K_1$、ドーナツの中央までの距離を$K_2$として上記の式を変形すると、以下のように求まります。
x'=\frac{K_{1} x}{K_2+z}, y'=\frac{K_{1} y}{K_2+z}
よって、点$(x,y,z)$はスクリーン上の$(\frac{K_{1} x}{K_2+z}, \frac{K_{1} y}{K_2+z})$の位置に投影されることになります。
ターミナル上に表示する場合は「上から何番目、左から何番目の文字に表示する」といった扱いになるため、小数点以下の値を四捨五入するなりして座標を整数値に変換し、ターミナル上の位置を改めて求める必要があります。
どの点を描画すべきかの判断
先ほど、ドーナツの表面上の各点を投影する位置を計算しました。
しかし、これらの点をすべて描画するべきではありません。
というのも、立体には「裏面」や、ほかの面によって隠された面があり、これらの点は本来見えないはずなので、描画してはいけないのです。
このように、本来見えていないはずの点の描画をスキップするために、深度情報を用います。
あるターミナル上の座標を考えた際、その座標に描画すべき点が複数あった場合、それぞれの視点からの距離(深度情報)を求めます。
視点から見える点は、これらの点の中で、最も視点からの距離が近い、つまり最も深度が浅い点のみになります。(それ以外の点は、最も震度が浅い点によって隠されている、と考えることができます。)
よって、最も震度が浅い点のみを描画し、それ以外の点の描画をスキップすればよい、ということになります。
コード上では、各点を描画すべき位置を計算したのちに、その位置の深度情報を確認しています。(ターミナル上の各座標の深度情報はz_bufferに記録されています)
もし、描画対象の点の深度がその位置に記録されている深度より浅かった場合は、深度情報を上書きし、点を描画します。
そうでなければ、点の描画をスキップする、という流れになっています。
表現する文字の選択
さて、ターミナル上に描画する際に、すべての点を同じ文字で表現すると、立体感が失われてしまいます。
そこで、物体の明るさによって文字を変えることで立体感を出していきます。
立体をターミナル上で描画する際は、明るい場所ではよりドットが多い文字を、暗い場所ではよりドットが少ない文字を使って明暗を表現していきます。
(暗い).,-~:;=!*#$@(明るい)
そのため、各点を描画する際にはその点における明るさの情報が必要です。
物体の表面上における明るさ(輝度)$L$は、拡散反射率を考慮しない場合、光源の明るさ$I$と物体表面の法線と光源方向のなす角度$\psi$から以下のように求められます。
L = I\cos \psi
上記の式からわかる通り、光源の明るさが一定である場合、物体の表面上の明るさは物体表面の法線と光源方向のなす角度から求めることができます。(物体表面の向きと光源の方向が一致しているほど、反射光も明るくなる、といったイメージです。)
この$\cos \psi$の値は、ベクトルの性質上、物体表面の単位法線ベクトルと光源方向の単位ベクトルの内積を計算することで求まります。
今回は、光源が我々のはるか後ろ斜め45度にあると仮定し、すべての点からの光源方向の単位ベクトルを$(0,\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}})$であると近似することにします。
物体上の表面上の各点における単位法線ベクトルは$[\cos \theta, \sin \theta, 0]$をx,y,z軸を中心としてそれぞれ回転させたものであり、これと$(0,\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}})$の内積を求めると・・・
L = \frac{1}{\sqrt{2}}(\cos \phi\cos\theta\sin B - \cos A \cos\theta \sin \phi - \sin A \sin \theta + \cos B (\cos A \sin \theta - \cos\theta\sin A \sin\phi))
となります。これが各点の明るさとなります。
Lは0~1の範囲の範囲をとるので、それに合わせて適切な文字を選択することで描画すべき文字を決定することができます。
ここまでのステップでターミナル上に描画すべき文字列が求まりました。
ターミナル上へのアニメーションの描画
ターミナル上にただ単に文字を出力するだけでは、表示が更新されず、ひたすら下に表示が追加されるだけになってしまいます。
それではアニメーションにならないので、エスケープシーケンスを用いて画面上の制御を行うことで、アニメーションの表示を実現します。
アニメーションの描画は、毎フレームごとに表示領域を上書きする方針で行い、大まかに①表示領域を確保する初期処理、②画面更新処理の2段階で行っています。
(ターミナル上の画面をフレームの描画ごとにクリアする方法もありますが、この方法では画面が非常にチカチカするため、今回は採用していません。)
初期処理
まず最初に描画領域を確保してしまいます。
今回のアニメーションでは、最大window_height行までしか描画されません。
そのため、あらかじめこの行数分だけ下にスクロールしておいて、その後先頭にカーソルを戻しておきます。
この時にカーソルの位置を記憶しておき、後で更新処理の際に利用します。
# あらかじめ表示する行数だけカーソルを下に移動させる
print(f"\033[{window_height}S", end="")
# 最初の行へ戻す
print(f"\033[{window_height}A", end="")
# 最初の行の位置を記憶しておく
print("\033[s", end="")
画面更新処理
更新処理では、初期処理で記憶した最初の行の位置にカーソルを移動させたのちに、フレームを書き込んでいきます。
# 記憶された情報をもとに最初の行の位置へ移動する
print("\033[u", end="")
print(img, flush=True)
お疲れさまでした。これで、ターミナル上でドーナツを回すことができるようになりました!
おわりに
今回のドーナッツのプログラムですが、立体状の点を計算してレンダリングする仕組みを応用すれば、ドーナツ以外の立体も表示できます。
応用ついでに試してみてはどうでしょうか?