この記事は freee 19新卒 Advent Calendar 2018 3日目の記事です.freee Developers Advent Calendar 2018 とか 裏freee developers Advent Calendar 2018 の内定者版ですね.
前回の記事はすぎけんKさんの【freee19新卒アドベントカレンダー】こころでした.DB ぶっこわし……怖いですね.僕もチームの NAS のアンマウントを忘れたままマウントポイントを rm -rf したことがあります.胃がヒュンってしました…….
はじめに
僕は,来年度から freee で新卒として働く予定の,くるぶしといいます.大学では主に形式言語をやっています.入社後も本名よりかニックネームで気軽に「くるぶし」と呼んでもらえるとうれしいです.推しは金剛いろはです.最近配信が少ないですが Земля Чан も好きです.
……タイトルがおかしい?それじゃフリーランスっぽい?……おっと,スペルミスです.free ではなくて freee でした.大変失礼しました.今後間違いがないよう,fre とか free を freee に変換する関数を作っておきましょう1.
q (f:xs) = f : q(xs)
q (r:xs) = r : q(xs)
q (e:xs) = e:e:e : q1(xs)
q ([]) = []
q1(f:xs) = f : q(xs)
q1(r:xs) = r : q(xs)
q1(e:xs) = q1(xs)
q1([]) = []
文字列から文字列への関数 q は free とか freeee とかを freee に変換します.文字列が f,r で始まる場合には f,r を出力して後続の文字列を q で再帰的に処理しますが,e から始まる場合には e を 3 つ出しておいて後続の文字列を q1 で処理します.関数 q1 は e の出現を無視する関数です.f,r が来ればそれを出力して q に戻ります.例えば入力が frefree の場合
q(f:r:e:f:r:e:e:[])
= f:q(r:e:f:r:e:e:[])
= f:r:q(e:f:r:e:e:[]) # e を発見したので eee 出力して q1 へ
= f:r:e:e:e:q1(f:r:e:e:[]) # e 以外を発見したので q へ
= f:r:e:e:e:f:q(r:e:e:[])
= f:r:e:e:e:f:r:q(e:e:[]) # e を発見したので eee 出力して q1 へ
= f:r:e:e:e:f:r:e:e:e:q1(e:[]) # e を無視
= f:r:e:e:e:f:r:e:e:e:q1([])
= f:r:e:e:e:f:r:e:e:e:[]
となり freeefreee が返ってきます.簡単ですね.でも本当に意図した通りの関数なのでしょうか.
"意図"の表現
関数 q は次の通りの意図で定義しました(簡単のため今後「繰り返し」を「0回以上の繰り返し」という意味で使います.クリーネスターですね).
命題:「入力文字列が fr{eの繰り返し} の繰り返しであるとき,出力文字列は freee の繰り返しになっている」
想定する入力文字列は fre やら freefreee やら freefreefree やら……と無限通りあります.そのため命題の真偽を調べるためには,無限通りのテストが必要に思えます.しかし,ああ,なんたる偶然!この真偽は僕が大学で学んでいた形式言語を用いると,有限時間で検査することができるのです.そのためにまず「想定する入出力文字列全体の(無限)集合」をオートマトンで表現してみます.
fr(eの繰り返し)の繰り返しなる文字列全体の集合は次のオートマトン A で表現できます.
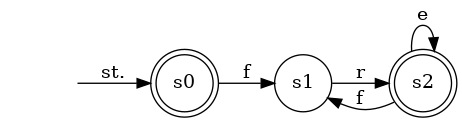
ひとつひとつの○を状態と呼び,特に◎を受理状態と呼びます.また矢印を遷移と呼びます.例えば文字列 free が与えらえたとき,s0 からはじめて辿りつく状態を調べてみます.
s0 -f-> s1 -r-> s2 -e-> s2 -e-> s2
で s2 に辿りつきました.s2 は受理状態なので「A は free を受理する」といいます.一方で文字列 frf ではどうでしょうか.
s0 -f-> s1 -r-> s2 -f-> s1
受理状態には辿りつけませんでした.このとき「A は frf を拒否する」といいます.ほか,遷移を辿れなくなっても(ff など)拒否といいます.
このように考えてみると,A は入力として想定した fr{eの繰り返し}の繰り返しのみを受理することが分かると思います.同様にして出力として想定した freee の繰り返しのみを受理するオートマトン B を作ってみましょう.

よさそうですね.
想定する文字列全体の(無限)集合は表現できました.では関数はどうでしょう.実は先程の関数 q はオートマトンに良く似たトランスデューサと呼ばれるもので表現することができます.q をトランスデューサ T で表現してみると
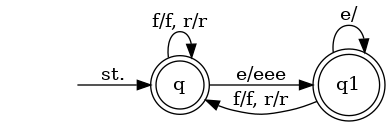
となります.オートマトンでは遷移に文字が1つ書かれていたのに対して,トランスデューサでは遷移に入力文字と出力文字列が/で書かれます./の左だけ見てオートマトンとして遷移を辿ったとき/の右側を出力文字列として扱います.例えば q -e/eee-> q1 は状態 q に対して文字 e が来たら eee を出力して q1 に遷移することを意味しています.これは q の定義
q (e:xs) = e:e:e : q(xs)
を表現しています.遷移ごとに得られる文字列の列びを最終的な出力結果とするならば T の遷移は q および q1 の定義と一致していることが分かります.例えば frefree が入力の場合
q -f/f-> q -r/r-> q -e/eee-> q1
-f/f-> q -r/r-> q -e/eee-> q1 -e/-> q1
と遷移し,出力は / の右側を結合した freeefreee となります.
型検査
任意のトランスデューサ T から得られる関数 τ,オートマトン A, B に対して「任意の文字列 w について A が w を受理するならば B は τ(w) を受理する」かどうかを調べることを型検査といいます.まさに調べたかった「w が fr{eの繰り返し}の繰り返しならば q(w) が freee の繰り返しになるか?」は型検査そのものです.そして型検査は有限時間で判定可能であることが知られています(というか気がつきます,詳しくは後述します).
ということで,実装しておきました.これです.コンパイル方法は Readme.md に書いておきました.さっそく検査してみましょう.先程の T や A,B を次のように書いて freee.tc で保存しておきます.
// typechecking test
transducer T = {
initial : [q],
accepted : [q,q1],
rules : [
q -f/[f]-> q,
q -r/[r]-> q,
q -e/[e,e,e]-> q1,
q1 -f/[f]-> q,
q1 -r/[r]-> q,
q1 -e/[]-> q1
]
}
automaton A = {
initial : [s0],
accepted : [s0,s2],
rules : [
s0 -f-> s1,
s1 -r-> s2,
s2 -e-> s2,
s2 -f-> s1
]
}
automaton B = {
initial : [s0],
accepted : [s0],
rules : [
s0 -f-> s1,
s1 -r-> s2,
s2 -e-> s3,
s3 -e-> s4,
s4 -e-> s0
]
}
typecheck T : A -> B
実際に検査してみます.
$ ./checker.byte < freee.tc
T: A -> B :false !
counter example is T(f,r) -> f,r
……なるほど.正しく定義できていませんでした.fr が反例のようです.
q(f:r:[])
= f:q(r:[])
= f:r:q([])
= f:r:[]
たしかに fr は fr(eの0回の繰り返し) になっていて出力が freee の繰り返しになっていません.盲点でした.定義を変えてみます.
p (f:xs) = f : p(xs)
p (r:xs) = r:e:e:e : p(xs)
p (e:xs) = p(xs)
p ([]) = []
さっきよりすっきり書けています.関数 p は r が来たところで reee までまとめて出力してしまい,e が来た場合にはそれを無視します.なんだか頼りない定義に見えますが,今度は正しいでしょうか.freee.tc に次を追記して検査してみます.
// typechecking test2
transducer T' = {
initial : [q],
accepted : [q,q1],
rules : [
p -f/[f]-> p,
p -r/[r,e,e,e]-> p,
p -e/[]-> p
]
}
typecheck T' : A -> B
$ ./checker.byte < freee.tc
T: A -> B :false !
counter example is T(f,r) -> f,r
T': A -> B :true !
こんどは意図通りに正しい関数が定義できているようです!
ほかにも気になる関数やオートマトンがあれば書いて調べてみてください.ただパーサが自作でボロボロなので,親切なエラーメッセージはでてきませんし,特に構文もまとめてません.がんばって察してください.詳しい方に向けに言っておくと,トランスデューサ,オートマトンともに非決定的な遷移にも対応しています.こんなのです.
rules : [
p -f/[f]-> p,
p -f/[f,f]-> p
]
技術的な話
どのようにして検査をしているのか,ざーっと概要だけ述べておきます.
オートマトンとトランスデューサに関して次の事実が知られています.
- オートマトン A,トランスデューサ T に対して,A が受理する文字列を T で変換した文字列を受理するオートマトンが構成できる(トランスデューサの像を表現します)
- オートマトン A に対して A が拒否する文字列を受理するオートマトンが構成できる(補集合です)
- 2つのオートマトン A,B に対して A も B も受理する文字列を受理するオートマトンが構成できる(積集合です)
- オートマトン A に対して,A が受理する文字列が存在するか否かが判定できる(空集合かどうかの判定です)
よって,オートマトンA,B,トランスデューサ T に対しては
- A 上の T の像を表現するオートマトン C を構成し,
- B が拒否する文字列を受理するオートマトン B' を構成し,
- C も B' も受理する文字列を受理するオートマトン D を構成し,
- D の空判定を行う
ことで,A が受理する文字列を T で変換した文字列でかつ B が拒否する文字列,つまり想定入力から変換された想定外出力が存在するか否かが検査可能になるわけです.例えば先程の q の検査では D の一部としてこんなのがでてきます.自動生成なので僕には読めませんが…….
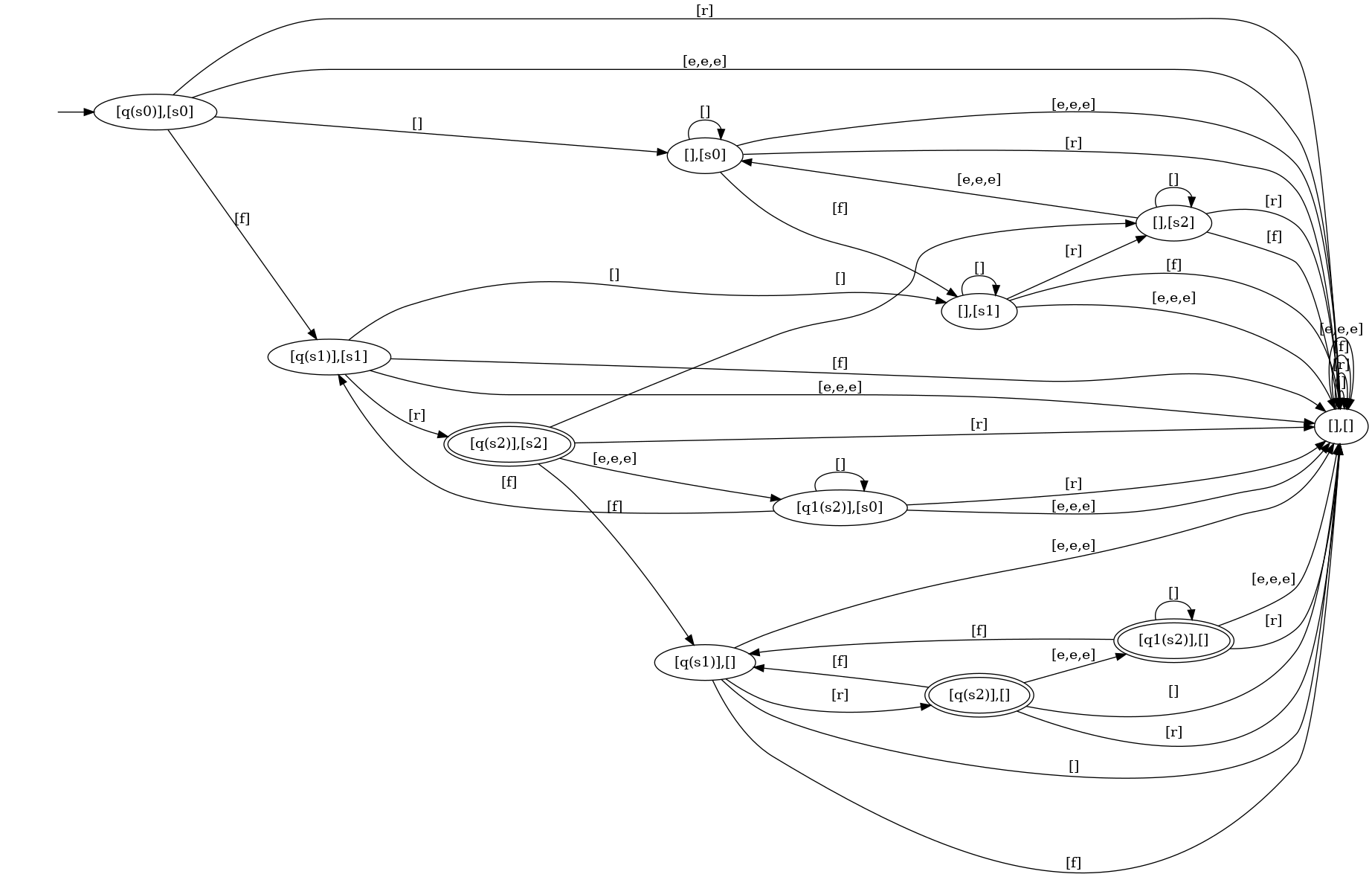
最終的な目標の空判定のためには C や D の構成を完全に行う必要がない場合もあります.今回の実装では on the fly にオートマトンの遷移を構成して高速化を狙っています.
トランスデューサは文字列から文字列への部分関数を表現していました.これを拡張し,木構造から木構造への関数を表現する(トップダウン)木トランスデューサや,さらに累積引数を追加したマクロ木トランスデューサなど,さまざまなものが考えられています.これら2に対しても,像を利用した方法ではないのですが3,型検査することができます.
まとめ
今回は free を freee に変換する関数 p を定義し,その正当性を調べてみました.ただし,入力は fr(eの繰り返し)の繰り返しと想定していました.f,r,e で構成される任意の文字列を入力として想定する場合には freee の繰り返しにはならないことは察しがつくと思います.このように,想定する入力によって「正しいか否か」は変ってくるわけです.
そういった意味で,関数を定義する際には「想定される入力」を常に意識し共有することが大切だと思っています.できればそれは「型」で表現するべきです.それが難しければ想定外の入力についてのエラー処理が必要です.想定する入力をコメントアウトで書いておくこともいいかもしれません.そこらへん気を付けられるエンジニアを目指します.
質問,アドバイス,つっこみ,オススメの VTuber 等ありましたら,気軽に @kurubushi312 にリプライ等をお願いします.freee 界隈の皆さんにいたっては,入社後見かけましたら気軽に「そういえばあの記事,〜〜だったよー」と絡んでもらえれば幸いです.修論進捗がヤバいですが,きっと卒業してみせるので.
次回の記事は足立さんの「えええ。ちょっとかたくない? – 暇つぶし。」です.
P.S.
想定される質問「正当性を示してくれる型検査器の正当性はどうやって示すのですか?」
ぼく「そこに気がつくとは……やはり天才か……」4
-
[x,y,z]なるリストをx:y:z:[]と書くことにします(Cons リストですね). ↩ -
文字列の(無限)集合をオートマトンで表現していたのに対して,ここでは木構造の(無限)集合を木オートマトンと呼ばれるもので表現します.オートマトンが正規表現に対応しているのに対して,木オートマトンは正規木表現に対応しています.正規木表現は,たとえば HTML や XML といった木構造の形を定義する DTD などに応用されています. ↩
-
木オートマトンでは像を表現しきれないのですが,なんと逆像は表現できます.そのためこの逆像を構成して検査に用いるのです.逆像の構成は inverse type inference,これを用いた型検査は inverse typechecking などと呼ばれています. ↩
-
Coq 等の定理証明支援系の上で実装すればたぶんいいかんじです.Coq の正しさについては Inria に任せます. ↩