※ちょっとコードを修正しました。2つ目のコード内のモジュールを調整し忘れてました。ごめんなさい
この記事は「農家経済シミュレーション①」の続きなので、先にそちらの記事の導入部分だけでも見ていただければ幸いです。
「……①」では、シミュレーション内部のモデルや、最終的に目指すところを説明しました。
ということで、
この「……②」では、自前で作った農家経済シミュレーションのコードを紹介します。
さっそく、「モデルの概説」「コード」「シミュレーション結果」を見ていきましょう!
環境情報
この記事は
python 3.8.3
scipy 1.5.0
をjupyter notebook上で使ってます。
(この書き方であってますか、、、?)
モデルの概説
農家行動の説明
農家は「労働力」と「農地」を有しており、それらを使って穀物Aを生産し、自分で食べたり、売ったり、買ったりします。
なお、穀物Aは飼料用トウモロコシをイメージし、場所はメキシコ農村部をイメージしてます。
同時に、農家は消費者でもあるので、自らの効用を最大化するように「余暇」と「その他の財」を消費します。
したがって、本シミュレーションでは「予算制約下における農家の効用最大化問題」がロジックの核となります。
また、Janvry(1991)に基づき、農家を以下3パターンに分けました。
net-seller=「穀物Aを自給したうえで余った分を売る」
自給農家=「穀物Aを完全に自給する」
net-buyer=「穀物Aを自給して、足りない分を他人から買う」
詳しいことは「……①」で説明したので、そちらをご確認ください。
コードのフローの説明
①Classを使って3パターンの農家行動を設定する。
②Classを使ってMarket(価格情報を保持する役)の設定をする。
③穀物Aの価格を1.5倍にする関数を作る。その他の財の価格を0.9倍にする関数を作る。穀物Aの価格を1.5倍にして、同時にその他の財の価格も0.9倍にする関数を作る。
④穀物A価格とその他の財価格を以下のように変動させる。注
1-10期:初期価格安定
11期:A価格増加
12-20期:価格安定
21期:その他の財価格減少
22-30期:価格安定
31期:Aとその他の財価格変化
32-40期:価格安定
⑤結果をリストに入れて出力。
注 長いスパンで安定期を取った理由は、このブログで行ったことの次の段階では価格以外の変数を変動させる予定があるからです。
コード
効用関数のパラメータを計算する
※データのダウンロードが面倒くさいと思いますので、ここを飛ばしても最終的なシミュレーションはできるようにしました。
まずは、メキシコ国家地理統計院(INEGI)が公開する2018年世帯消費調査(ENIGH)の"trabajos_2018.csv"、"poblacion_2018.csv"、"concentradohogar_2018.csv"を
今開いているディレクトリの中に入れます。
https://www.inegi.org.mx/programas/enigh/nc/2018/
次に、以下のコードを実行します。
# モジュールのインポート
import numpy as np
import pandas as pd
from tqdm import tqdm_notebook as tqdm
# 効用関数で使うパラメータの推計
# 週当たり労働時間の合計値(多分、成人構成員の労働時間総計だと思う)
tr_ori = pd.read_csv("trabajos_2018.csv", usecols=["folioviv", "htrab"])
# foliovivが重複していた。多分、同じ家内の違う世帯が分けられている。これを足す。
# 箱を作る
tr = pd.DataFrame(np.arange(4).reshape(2,2), columns=["folioviv", "htrab"], index=[1, 2])
tr = tr.drop(tr.index[[0, 1]])
tr = tr.reset_index(drop=True)
# ユニークなfoliovivごとに和を計算して、箱に入れる。
vivs = tr_ori["folioviv"].unique()
vivs = vivs.tolist()
for viv in tqdm(vivs):
trr = tr_ori[tr_ori["folioviv"]==viv]
htrab = trr["htrab"].sum()
# アペンド
tr = tr.append({"folioviv":viv, "htrab":htrab}, ignore_index=True)
# 費用
"""
mayores:12歳以上構成員、ing_cor:月総収入、trabajo:月自営業以外で働いて得た収入、negocio:月自営業収入、vesti_calz:衣類に使った総費用、
salud:医療系に使った総費用、foraneo:海外輸送費、mantenim:自動車系、comunica:情報伝達、educa_espa:教育とフィエスタなど
"""
co = pd.read_csv("concentradohogar_2018.csv", usecols=["folioviv", "tam_loc", "mayores", "ing_cor", "trabajo", "negocio", "frutas", "azucar",
"cafe", "bebidas", "tabaco", "vesti_calz", "salud", "foraneo", "mantenim",
"comunica", "educa_espa"])
# 州の識別子
pb = pd.read_csv("poblacion_2018.csv", usecols=["folioviv", "residencia"])
# dfの結合
df = pd.merge(co, pb, on="folioviv")
df = pd.merge(df, tr, on="folioviv")
df = df[~df.duplicated()] # なぜか重複業があったので、重複行を消した
df = df[df["residencia"]!=" "] # なぜか州が空白""になる場合があったので、その行を消した
df = df[df["tam_loc"]!=1] # 対象地域を田舎に限定
df = df[df["tam_loc"]!=2]
# 割と娯楽に近いと判断した消費額の総計
df["sum_cons"] = df["frutas"] + df["azucar"] + df["cafe"] + df["bebidas"] + df["tabaco"] + df["vesti_calz"] + df["salud"] + df["foraneo"] + df["mantenim"] + df["comunica"] + df["educa_espa"]
# 自営業かどうか識別
df["self"] = (df["negocio"] > 0) * 1
# 非自営業者の賃金の平均値を求める
nonself = df[df["self"]==0]
wage = (nonself["trabajo"].sum() / 30) / (nonself["htrab"].sum() / 7) # 収入は月当り、労働時間は週当たりなので、日当たりに修正
# 世帯当たり、日当たり、余暇時間を計測。余暇時間=大人世帯員数×24 - 世帯労働時間/7 - 大人世帯員数×睡眠時間(6)
df["leisure"] = df["mayores"] * 24 - df["htrab"] / 7 - df["mayores"] * 6
# 余暇を取ることで犠牲にした月当たり収入を計算
df["opportunity"] = df["leisure"] * wage * 30
# その他消費財と余暇で犠牲にした収入が総収入+犠牲にした収入の何割を占めるか計算(全体平均)
income = df["ing_cor"].sum() + df["opportunity"].sum()
consumption = df["sum_cons"].sum()
opportunity = df["opportunity"].sum()
con_in = consumption / income
opp_in = opportunity / income
これによって、
「田舎、自営業者を除く平均賃金(時給)」 = 75.25114451327885
「余暇を過ごす際の機会費用 / 総消費額」 = 0.7171948682330835
「生活必需品でない財の総消費額 / 総消費額」 = 0.06287930254251227
が得られました。
本シミュレーションでは、効用は2次式モデルで表され、↑で求めた後者2つが効用関数のパラメータとして使われます。
この方法が理論的に間違っていることを含めて、詳しいことは「……①」で説明したので、そちらをご確認ください。
なお、以上に示したコードをわざわざ実行しなくても、次に続くコードでは↑の数値自体を打ち込んでます。
メイン実行部分
冒頭で設定したグローバル変数の大半は実際のデータから引用しました。
どのようなデータを使ったのかは、「……①」をご確認ください。
①自給農家
↓ちょっと修正しました(tqdmをはじめにimportし忘れてたので、追加しました)
# モジュールのインポート
from tqdm import tqdm_notebook as tqdm
from scipy.optimize import minimize
# グローバル変数(4か月を1サイクルとする)
ao = 0.06 # その他の財を消費するときの係数(0.06)
al = 0.72 # 余暇を消費するときの係数(0.72)
aoo = 0.01 # その他の財だけ消費するときの係数(休む暇がなくてつらいから低め)
aLl = 0.01 # 余暇だけ消費するときの係数(遊ぶものが無くて暇なので低め)
aol = 0.15 # まんべんなく使えるときのうれしさ
w = 75.3 # 賃金(時給)
tw = 20 # 労働市場で労働を売る際にかかる単位当たり取引費用
ta = 5024207380 / 8324248200 / 10 # Aを売るときの取引費用(価格の10分の1と簡単に設定)
r = 2000 * 4 # 地価(4か月一括で借りる前提の地代)
SEED = 12345 # シード値
R = 40 # 繰り返し回数の設定
L = (24 - 6) * 30 * 4 # 初期賦存労働力(4か月あたり時間)
Yield = 5024207380 / 396397.92 # 単収(kg / ha)
Equip = 1 / 52 # 土地装備率(ha / 時間)
appe = 0.25 * 30 * 4 # 満腹制約(4か月当たりに食べる量)
price0 = 5024207380 / 8324248200 # 作物価格(peso/ha)
milk_meat = 130/4 + 25/4 # 食費
# クラス定義
class Autarky:
"""自給的農家を表現するクラスの定義"""
def __init__(self, cat): # コンストラクタ
self.category = cat
self.oriA = 2 # 保有土地面積(ha)
self.oriL = L # 保有労働時間
self.utility = 0 # 最大効用(ひとまず0)
self.co = 0 # 効用最大時のOの消費量
self.l = 0 # 効用最大時の余暇時間
self.C = 0 # 効用最大時の総消費額
self.profit = 0 # 効用最大時の利潤
self.qa = 0 # 効用最大時のAの生産量
self.LA = 0 # 以下、効用最大時の各生産要素の使用量
self.AA = 0
self.Ln = 0
self.An = 0
"""
効用最大化問題
x = [co, La, Ln, l, Aa, An]
"""
def solveUmax(self, Market): # 利潤を最良化するようにAとBを生産する
pA = Market.pA
po = Market.po
oriA = self.oriA
oriL = self.oriL
"""効用関数"""
def utility(x): # 二次式モデル
return -1 * (ao*x[0] + al*x[3] + 1/2*(aoo*x[0]*x[0] + aLl*x[3]*x[3] + aol*x[0]*x[3]))
"""流動性制約"""
def cons_liquidity(x):
return (w - tw) * x[2] + r * x[5] - po * x[0] - milk_meat
"""空腹制約"""
def appetite(x):
return Yield * Equip * x[1] - appe
"""土地面積と投入労働力の関係性"""
def labor_land(x):
return x[4] - Equip * x[1]
"""賦存要素制約"""
def labor_cons(x):
return oriL - x[1] - x[2] - x[3]
def land_cons(x):
return oriA - x[4] - x[5]
"""各変数の符号制約"""
def co(x):
return x[0]
def La(x):
return x[1]
def Ln(x):
return x[2]
def l(x):
return x[3]
def Aa(x):
return x[4]
def An(x):
return x[5]
cons = ({"type": "ineq", "fun": cons_liquidity}, {"type": "ineq", "fun": appetite}, {"type": "ineq", "fun": labor_land},
{"type": "ineq", "fun": co}, {"type": "ineq", "fun": La}, {"type": "ineq", "fun": Ln}, {"type": "ineq", "fun": l},
{"type": "ineq", "fun": Aa}, {"type": "ineq", "fun": An}, {"type": "eq", "fun": labor_cons},
{"type": "ineq", "fun": land_cons})
# Aの生産に要素を全部りしている状態を初期値とする。
x0 = [0, oriL, 0, 0, oriA, 0]
res = minimize(utility, x0, constraints=cons, method="SLSQP") # 最適化問題を解くコマンド
# 結果が負になったときの対応
while (res.x[0] < 0) or (res.x[1] < 0) or (res.x[2] < 0) or (res.x[3] < 0) or (res.x[4] < 0) or (res.x[5] < 0):
x0 = []
for X in res.x:
if X < 0:
X = 0
x0.append(X)
res = minimize(utility, x0, constraints=cons, method="SLSQP")
"""計算した結果をしまっていく"""
self.LA = res.x[1]
self.Ln = res.x[2]
self.AA = res.x[4]
self.An = res.x[5]
self.co = res.x[0]
self.l = res.x[3]
self.utility = - 1 * res.fun
self.profit = (w - tw) * res.x[2] + r * res.x[5]
self.qa = Yield * Equip * res.x[1]
self.C = po * res.x[0]
# クラスAutarkyの定義終わり
# クラス定義 Market
class Market:
def __init__(self):
self.pA = price0
self.po = 30
def price_A(self): # pAが1.5倍に値上げ
self.pA *= 1.5
def price_o(self): # poが90%に値下げ
self.po *= 0.9
# クラスMarketの定義終わり
# 下請け関数の定義
# 価格無変化時における次期の計算を統括するcalcn_n()関数の定義
def calcn_n(t, a, Market):
# ①今期初めにおける価格をリストに入れる
pAlist.append(Market.pA)
polist.append(Market.po)
tlist.append(t) # 時間
# ②自給的農家の効用最良化
for i in range(len(a)):
a[i].solveUmax(Market)
# pAが1度変化した時における次期の計算を統括するcalcn_A()関数の定義
def calcn_A(t, a, Market):
# ①pB価格の変化
Market.price_A()
# ②今期初めにおける価格をリストに入れる
pAlist.append(Market.pA) # 価格
polist.append(Market.po)
tlist.append(t) # 時間
# ③農家の効用最良化
for i in range(len(a)):
a[i].solveUmax(Market)
# poが1度変化した時における次期の計算を統括するcalcn_o()関数の定義
def calcn_o(t, a, Market):
# ①po価格の変化
Market.price_o()
# ②今期初めにおける価格をリストに入れる
pAlist.append(Market.pA) # 価格
polist.append(Market.po)
tlist.append(t) # 時間
# ③農家の効用最良化
for i in range(len(a)):
a[i].solveUmax(Market)
# pAとpoが1度変化した時における次期の計算を統括するcalcn_Ao()関数の定義
def calcn_Ao(t, a, Market):
# ①pAとpo価格の変化
Market.price_A()
Market.price_o()
# ②今期初めにおける価格をリストに入れる
pAlist.append(Market.pA) # 価格
polist.append(Market.po)
tlist.append(t) # 時間
# ③農家の効用最良化
for i in range(len(a)):
a[i].solveUmax(Market)
# 要素の集計値計算及びリストへの追加を行うCalc_list()関数の定義
def calc_list(a):
qa = 0
profit = 0
LA = 0
Ln = 0
AA = 0
An = 0
l = 0
co = 0
utility = 0
C = 0
for i in range(len(a)):
qa += a[i].qa
profit += a[i].profit
LA += a[i].LA
AA += a[i].AA
Ln += a[i].Ln
An += a[i].An
l += a[i].l
co += a[i].co
utility += a[i].utility
C += a[i].C
utilitylistA.append(utility)
colistA.append(co)
ClistA.append(C)
profitlistA.append(profit)
qalistA.append(qa)
LAlistA.append(LA)
AAlistA.append(AA)
AnlistA.append(An)
LnlistA.append(Ln)
llistA.append(l)
# メイン実行部
# 初期化
Market = Market() # 変数にクラスMarketのインスタンスを入れる
# リストの中にカテゴリ0のAutarkyのインスタンスを複製生成(する予定。今回は一人ずつ)
a = [Autarky(0)]
# 農家の状態のリスト化
utilitylistA = []
ca_plistA = []
colistA = []
ClistA = []
profitlistA = []
qalistA = []
qblistA = []
LAlistA = []
AAlistA = []
AnlistA = []
LnlistA = []
llistA = []
# 価格と生産物の余りのリスト化
pAlist = []
polist = []
# 時間のリスト
tlist = []
# シミュレーション
for t in tqdm(range(R)):
if t <= 10: # 1~10期:初期価格
calcn_n(t, a, Market)
calc_list(a)
if t == 11: # 11期:A価格変化
calcn_A(t, a, Market)
calc_list(a)
if (t > 11) and (t <= 20): # 12~20期:A価格変化後の安定
calcn_n(t, a, Market)
calc_list(a)
if t == 21: # 21期:o価格変化
calcn_o(t, a, Market)
calc_list(a)
if (t > 21) and (t <= 30): # 22~30期:o価格変化後の安定
calcn_n(t, a, Market)
calc_list(a)
if t == 31: # 31期:Aとo価格変化
calcn_Ao(t, a, Market)
calc_list(a)
if (t > 31) and (t <= 40): # 32~40期:Aとo価格変化後の安定
calcn_n(t, a, Market)
calc_list(a)
# シミュレーションパートの終わり
# 重要な変数のリストをそのまま表示
print("収入",profitlistA,"\n","\n","A生産",qalistA,"\n","\n","LA",LAlistA,"\n","\n","Ln",LnlistA,"\n","\n","l", llistA, "\n","\n",
"A農地", AAlistA, "\n","\n","貸出農地",AnlistA, "\n","\n","効用",utilitylistA, "\n","\n", "o消費",colistA,"\n","\n","C",ClistA, "\n","\n",
"pA",pAlist,"\n","\n","po",polist)
# sell&buy.py
②net-seller
①自給農家でお見せしたコードの「# クラス定義 // Class Autarky: ~ # クラスAutarkyの定義終わり」までの部分を以下のコードに変えてください。
# クラス定義
class Seller:
"""自給的農家を表現するクラスの定義"""
def __init__(self, cat): # コンストラクタ
self.category = cat
self.oriA = 2 # 保有土地面積
self.oriL = L # 保有労働時間
self.utility = 0 # 最大効用(ひとまず0)
self.co = 0 # 効用最大時のOの消費量
self.l = 0 # 効用最大時の余暇時間
self.C = 0 # 効用最大時の総消費額
self.profit = 0 # 効用最大時の利潤
self.qa = 0 # 効用最大時のAの生産量
self.LA = 0 # 以下、効用最大時の各生産要素の使用量
self.AA = 0
self.Ln = 0
self.An = 0
"""
効用最大化問題
x = [co, La, Ln, l, Aa, An]
"""
def solveUmax(self, Market): # 利潤を最良化するようにAとBを生産する
pA = Market.pA
po = Market.po
oriA = self.oriA
oriL = self.oriL
"""効用関数"""
def utility(x): # 二次式モデル
return -1 * (ao*x[0] + al*x[3] + 1/2*(aoo*x[0]*x[0] + aLl*x[3]*x[3] + aol*x[0]*x[3]))
"""流動性制約"""
def cons_liquidity(x):
return (pA - ta) * (Yield * Equip * x[1] - appe) - po * x[0] - (w + tw) * x[2] - r * x[5] - milk_meat
"""空腹制約"""
def appetite(x):
return Yield * Equip * x[1] - appe
"""土地面積と投入労働力の関係性"""
def labor_land(x):
return x[4] + x[5] - Equip * (x[1] + x[2])
"""賦存要素制約"""
def labor_cons(x):
return oriL - x[1] - x[3]
def land_cons(x):
return oriA - x[4]
"""各変数の符号制約"""
def co(x):
return x[0]
def La(x):
return x[1]
def Ln(x):
return x[2]
def l(x):
return x[3]
def Aa(x):
return x[4]
def An(x):
return x[5]
def Anmax(x):
return 100 - x[5]
cons = ({"type": "ineq", "fun": cons_liquidity}, {"type": "ineq", "fun": appetite}, {"type": "ineq", "fun": labor_land},
{"type": "ineq", "fun": co}, {"type": "ineq", "fun": La}, {"type": "ineq", "fun": Ln}, {"type": "ineq", "fun": l},
{"type": "ineq", "fun": Aa}, {"type": "ineq", "fun": An}, {"type": "eq", "fun": labor_cons},
{"type": "ineq", "fun": land_cons}, {"type": "ineq", "fun": Anmax})
# Aの生産に要素を全部りしている状態を初期値とする。
x0 = [0, oriL, 0, 0, oriA, 0]
res = minimize(utility, x0, constraints=cons, method="SLSQP") # 最適化問題を解くコマンド
# 結果が負になったときの対応
while (res.x[0] < 0) or (res.x[1] < 0) or (res.x[2] < 0) or (res.x[3] < 0) or (res.x[4] < 0) or (res.x[5] < 0):
x0 = []
for X in res.x:
if X < 0:
X = 0
x0.append(X)
res = minimize(utility, x0, constraints=cons, method="SLSQP")
# 農地投入がかなり大きいのに、労働投入が0になったときの対応(初期値をちょっと変えてやりなおし)
if (res.x[1] <= 0) and (res.x[4] > 1):
x0 = [0, oriL - 1, 0, 1, Equip * (oriL - 1), 0]
res = minimize(utility, x0, constraints=cons, method="SLSQP")
# 結果が負になったときの対応2
while (res.x[0] < 0) or (res.x[1] < 0) or (res.x[2] < 0) or (res.x[3] < 0) or (res.x[4] < 0) or (res.x[5] < 0):
x0 = []
for X in res.x:
if X < 0:
X = 0
x0.append(X)
res = minimize(utility, x0, constraints=cons, method="SLSQP")
"""計算した結果をしまっていく"""
self.LA = res.x[1]
self.Ln = res.x[2]
self.AA = res.x[4]
self.An = res.x[5]
self.co = res.x[0]
self.l = res.x[3]
self.utility = - 1 * res.fun
self.profit = (pA - ta) * (Yield * Equip * res.x[1] - appe)
self.qa = Yield * Equip * res.x[1]
self.C = po * res.x[0] + (w + tw) * res.x[2] + r * res.x[5]
# クラスSellerの定義終わり
次に、「# メイン実行部」以下4行目の
a = [Autarky(0)]
を
a = [Seller(0)]
にしてください。
③net-buyer
①自給農家でお見せしたコードの「# クラス定義 // Class Autarky: ~ # クラスAutarkyの定義終わり」までの部分を以下のコードに変えてください。
# クラス定義
class Buyer:
"""自給的農家を表現するクラスの定義"""
def __init__(self, cat): # コンストラクタ
self.category = cat
self.oriA = 2 # 保有土地面積
self.oriL = L # 保有労働時間
self.utility = 0 # 最大効用(ひとまず0)
self.co = 0 # 効用最大時のOの消費量
self.ca = 0
self.l = 0 # 効用最大時の余暇時間
self.C = 0 # 効用最大時の総消費額
self.profit = 0 # 効用最大時の利潤
self.qa = 0 # 効用最大時のAの生産量
self.LA = 0 # 以下、効用最大時の各生産要素の使用量
self.AA = 0
self.Ln = 0
self.An = 0
"""
効用最大化問題
x = [co, La, Ln, l, Aa, An, ca]
"""
def solveUmax(self, Market): # 利潤を最良化するようにAとBを生産する
pA = Market.pA
po = Market.po
oriA = self.oriA
oriL = self.oriL
"""効用関数"""
def utility(x): # 二次式モデル
return -1 * (ao*x[0] + al*x[3] + 1/2*(aoo*x[0]*x[0] + aLl*x[3]*x[3] + aol*x[0]*x[3]))
"""流動性制約"""
def cons_liquidity(x):
return (w - tw) * x[2] + r * x[5] - po * x[0] - (pA + ta) * x[6] - milk_meat
"""空腹制約"""
def appetite(x):
return Yield * Equip * x[1] + x[6] - appe
"""土地面積と投入労働力の関係性"""
def labor_land(x):
return x[4] - Equip * x[1]
"""賦存要素制約"""
def labor_cons(x):
return oriL - x[1] - x[2] - x[3]
def land_cons(x):
return oriA - x[4] - x[5]
"""各変数の符号制約"""
def co(x):
return x[0]
def La(x):
return x[1]
def Ln(x):
return x[2]
def l(x):
return x[3]
def Aa(x):
return x[4]
def An(x):
return x[5]
def ca(x):
return x[6]
cons = ({"type": "ineq", "fun": cons_liquidity}, {"type": "ineq", "fun": appetite}, {"type": "ineq", "fun": labor_land},
{"type": "ineq", "fun": co}, {"type": "ineq", "fun": La}, {"type": "ineq", "fun": Ln}, {"type": "ineq", "fun": l},
{"type": "ineq", "fun": Aa}, {"type": "ineq", "fun": An}, {"type": "ineq", "fun": ca}, {"type": "eq", "fun": labor_cons},
{"type": "ineq", "fun": land_cons})
# Aの生産に要素を全部りしている状態を初期値とする。
x0 = [0, oriL, 0, 0, oriA, 0, 0]
res = minimize(utility, x0, constraints=cons, method="SLSQP") # 最適化問題を解くコマンド
# 結果が負になったときの対応
while (res.x[0] < 0) or (res.x[1] < 0) or (res.x[2] < 0) or (res.x[3] < 0) or (res.x[4] < 0) or (res.x[5] < 0):
x0 = []
for X in res.x:
if X < 0:
X = 0
x0.append(X)
res = minimize(utility, x0, constraints=cons, method="SLSQP")
"""計算した結果をしまっていく"""
self.LA = res.x[1]
self.Ln = res.x[2]
self.AA = res.x[4]
self.An = res.x[5]
self.co = res.x[0]
self.ca = res.x[6]
self.l = res.x[3]
self.utility = - 1 * res.fun
self.profit = (w - tw) * res.x[2] + r * res.x[5]
self.qa = Yield * Equip * res.x[1]
self.C = po * res.x[0] + (pA + ta) * res.x[6]
# クラスBuyerの定義終わり
次に、「# メイン実行部」以下4行目の
a = [Autarky(0)]
を
a = [Buyer(0)]
にしてください。
結果
上のコードを実行すると、最適解である各選択変数の各時期における値がリストで返ってきます。
それでは、せっかくシミュレーション結果が得られたので、
収入と効用に着目して、「自給農家」「net-seller」「net-buyer」を比較してみましょう!
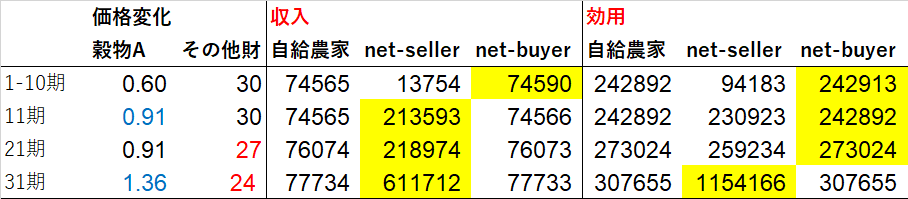
収入と効用の比較結果
表中「収入」「効用」について、3種類の農家を比べたコラムでは、各期において最も値が大きいセルを黄色で塗りました。
この表から分かることを「収入」と「効用」に分けて考察しました。
〇収入に着目:net-sellerは価格の変化に反応しやすい
まず、
初期時点において、net-sellerの収入が他の2種類の農家の6分の1程度しかないことが分かります。
初期時点の価格は現実をまあまあ反映してますので、この結果が示すことは、
「2haの農地で飼料用トウモロコシを作ってる単作農家は、農業を辞めたら収入が6倍になる」という事です。
実際は、2haくらいの農地を所有する農家は換金作物なども作っているため、もう少しマシな状況ですが、如何に農家の置かれる状況が悪いかが分かりますね。なるほど、離農者が続出するわけだ。
次に、
「収入」を見てみると、net-sellerの値が上がりまくってることが分かります。価格が1.5倍になったとき、収入は10倍以上になりました。
実は、この背景で、net-sellerは「余暇」の時間をどんどん削りまくって穀物A栽培に投入しまくってます。農産物価格が上がったから、仕事をしまくったわけですね。
したがって、市場に農産物の売り手として参加する農家は、農産物価格に過敏に反応するという事が分かりました。
自然な結果ですが、もしもnet-sellerが「自給農家」や「net-buyer」に変身できるとしたら、その農家は価格変動に弱い「net-seller」を続けたいと思いますかね?
net-sellerが価格変化に過敏すぎるという点も離農の一員なのかもしれません。
〇効用に着目:net-buyerになるのが一番効用が高い
まず、自給農家とnet-buyerの効用(と収入)がほとんど同じになった理由を説明します。
これは、自分ひとり分の穀物Aを自給するのは非常に簡単であるという事を示します。
表中には載せてませんが、自給農家が穀物Aの栽培に配分した農地は、0.0023ha = 0.23a = 23m^2でした。費やした時間は0.12時間 = 7.2分でした。
ここで想定したのは飼料用トウモロコシだったので、大規模機械などを使うことによって、人が食べるトウモロコシより大規模に生産される可能性があります。
また、1人が自給する分だけのトウモロコシを作る状況下において、同じ状況が再現されるか分かりません。
しかし、いずれにせよ、トウモロコシ栽培は結構お手軽だという事は言えそうですね。
日本における米栽培の利点も、時間をかけないで作ることができるので、兼業に向いていることだと言われます。
次に、真ん中の次期のnet-sellerとその他の農家を比べると可哀そうな事実に気づきます。
net-sellerの収入はその他の農家の収入の3倍なのに、効用がほとんど同じですね。
これは、net-sellerが働きすぎて、余暇が極めて少ない事を示唆しています。
いずれにせよ、この世界のnet-sellerがその他の農家と同じくらいの効用を得るには、穀物Aの初期価格を1.5倍に引き上げて、
余暇を減らして収入を3倍に引き上げる必要があるということが分かりました。
さいごに
ということで、今回は農家経済シミュレーションのコードと結果を確認しました。
シミュレーション結果から、いかにnet-sellerが可哀そうなのか分かりましたね(笑)
今後の課題としては、まず、もう少しパラメータの調整を頑張ってみて、現実に近い初期設定を実現させたいです。
なんとなく、賃金が高すぎるような気がしますね。
あとは、複合栽培と、作付け面積当たり一定額支給される補助金を組み込めないか検討してみます。
そのあと、ついにマルチエージェントシミュレーションを作り始めようと思います。
現状において答え(コード)が見えないのが、多数の農家が同じフィールドでわちゃわちゃ動くゲームを作るときに、各農家間のやりとりにおける着地点=価格や契約をマッチングさせる方法です。
価格や契約は、需要=供給、Aの利得=Bの利得、で決まるはずなのですが、さて、どんなコードを書けばそういう動きをしてくれるのか、、、。
ま、とりあえずなんかそれっぽい感じで作ってみます。
ここまで読んでいただいた方、ありがとうございました!