対象者
本記事は理論的なお話ですので、実装ベースで学習中の人はスルーしてくださっても大丈夫です。
「ディープラーニングと物理学」という本に書かれている内容(本記事では2章について)について、自分なりに解釈したものをなぐり書きしています。物理の視点から深層学習に切り込んでいてなかなか面白い本でした。理論ばっかりですが全体的にかなり噛み砕いて説明してありますので、そんなに読みにくい印象はないですね。もちろん理解できるかは別の問題です泣
目次
数学的な定式化
まずは必要な定式化を行います。
機械学習の目的は「未知のデータに対する予測を得ること」ですね。この時重要なのは 「私たちは与えられた環境(ルール)に関する知識を持っていない」 という前提があることです。
例えばサイコロのそれぞれの目の出る確率は同様に確からしく$\frac{1}{6}$である、なんてのは自明ですよね。このような場合に機械学習でサイコロの目の出る確率を探る必要は皆無なわけです。
しかし手書き数字認識などの、人間でもどうやって認識しているのか明確にアルゴリズム化できないような場合など、現実にはたくさんの「ルールに対する知識がない」状態があります。そのような状態に対して機械学習を用いる意味があるんですね。
ただ先の例のサイコロについても、「サイコロ」そのものを隠蔽してしまえば途端に「ルールに対する知識がない」状態を作り出すことが可能です。
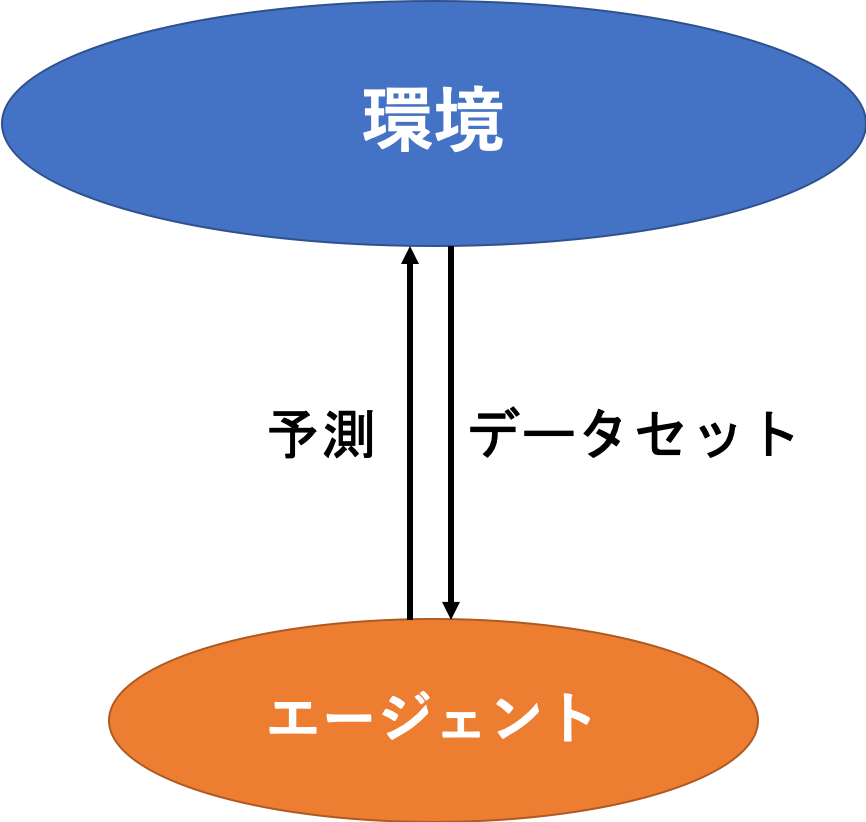
こんな感じで、環境からはデータセットが与えられ、エージェント(機械学習のモデル)がそこから予測する、というような感じですね。
与えられたデータセットというのがいわゆる経験です。とりあえず今回はデータセットとして$$\{ (x[i], d[i]) \}_{i=1, 2, \ldots, N}$$が与えられていることにします。
このデータセットからデータ$(x, d)$が得られる、という経験確率$$\hat{P}(x, d) = \cfrac{n(x, d)}{n(U)}$$が定義できます。ここで
- $n(•)$ : データの個数
- $U$ : データセット全体集合
としています。
ところでそもそもの「環境が与えるデータセットがどのように生成されているのか(つまりルール)」をデータ生成確率として$$P(x, d)$$のように定義しておきます。ちなみにこのデータ生成確率が存在することを仮定しています。存在しないと議論が発展しないですしね〜
このデータ生成確率は、少なくともエージェントは知り得ない情報となっています。
そして、環境がデータセットを作成することをサンプリングといい、$$(x[i], d[i]) \sim P(x, d)$$と書きます。
補足ですが、データセットが十分大きければエージェントが$P(x, d)$を正確に予測することが可能なことは大数の法則から示されます。
さて、エージェントを具体化していきましょう。
エージェントが$P(x, d)$を近似的に知るためには、エージェントが持つパラメータ$J$に依存する経験確率$$Q_J(x, d)$$を、パラメータ$J$を調整することで$P(x, d)$へと漸近させる必要があります。
この過程を一般に学習や訓練と呼びます。
学習が進んでいるかを知るために、$Q_J(x, d)$と$P(x, d)$とのある意味での距離を測る関数が必要です。ここで用いられるのが相対エントロピー1$$D_{KL}(P\|Q_J) = \sum_{x, d}{P(x, d) \log{\cfrac{P(x, d)}{Q_J(x, d)}}}$$です。$P\|Q_J$は$P$と$Q_J$の引数が非対称であることを強調するための記法です。
$D_{KL} \ge 0$なので、相対エントロピーが最も小さくなる時は等号成立時であり、その時$P(x, d) = Q_J(x, d)$であることが示せます。つまり、相対エントロピーを小さくする方に学習すれば学習が進んでいることになります。そのため、この相対エントロピー(またはその期待値)を汎化誤差と言います。
しかしこの汎化誤差にはデータ生成確率が使われているため、そのまま指標として用いることができません。
そのため代わりに先に定義した経験確率$\hat{P}(x, d)$を用いた経験誤差$$D_{KL}(\hat{P} \| Q_J) = \sum_{x, d}{\hat{P}(x, d) \log{\cfrac{\hat{P}(x, d)}{Q_J(x, d)}}}$$が用いられます。
エージェントのやることは汎化誤差を減少させることですが、実際に指標として用いることができるのは経験誤差です。そのため、経験誤差を減少させることが必ずしも汎化誤差を減少させる結果につながらないことがあるのがお分かりかと思います。このように、経験誤差ばかりが極端に小さくなることを過学習といいます。
VC次元
議論を進めるために、ここで重要な指標であるVC次元という考え方を導入します。
関連するお話として極限同定とかPAC学習とかがあるようですが、極限同定は全くわからないのでスルーしておきます...まずはPAC学習について。
PACモデル
確率的近似学習モデル(PAC Model: Probably Approximately Correct Model)は、仮説集合が有限な場合の学習可能性を扱うためのモデルです。とりあえず言葉の定義から。
仮説
機械学習における仮説とは、まあ簡単に言うと入力から出力を生成する写像(関数)のことを言います。
f: x \rightarrow y, \quad x \in R^d, y \in R^D
ある目的関数を近似しようとしているニューラルネットワークであったり、決定木であったり、そういった「機械学習のモデルそのもの」という認識でいいと思います。
仮説集合
仮説集合は文字通り仮説の集まり(集合)です。先の「仮説は機械学習のモデルそのもの」という認識で言うと、独立して学習されたモデルの集合です。例えばニューラルネットワークで言うならそれぞれの重みとバイアスが微妙に異なるモデルたちです。
F = \{f \mid f(W, x) = Wx, W \in R^{D \times d} \}
上式はある機械学習モデルを$f(W, x) = Wx$とした場合の式です。
機械学習とは何らかの手法で仮説集合から良いモデルを探し出すことを言います。
さて、PACモデルを考えるモチベーションは、極限同定のように汎化誤差をゼロにする場合を考えるのではなく、まあまあ良い学習をするために必要な学習データについて議論したいということです。
詳しくはこれなどを見てください。
PACモデルの問題点とVC次元
PACモデルの議論は「仮説集合が有限である」という前提があります。つまり、例えばニューラルネットワークなどの、重みやバイアスにより仮説を生成する学習モデルではうまく議論できないのです。これを改善するために導入する考え方が VC次元(Vapnik-Chervonenkis dimension) です。直感的には下図のような感じです。
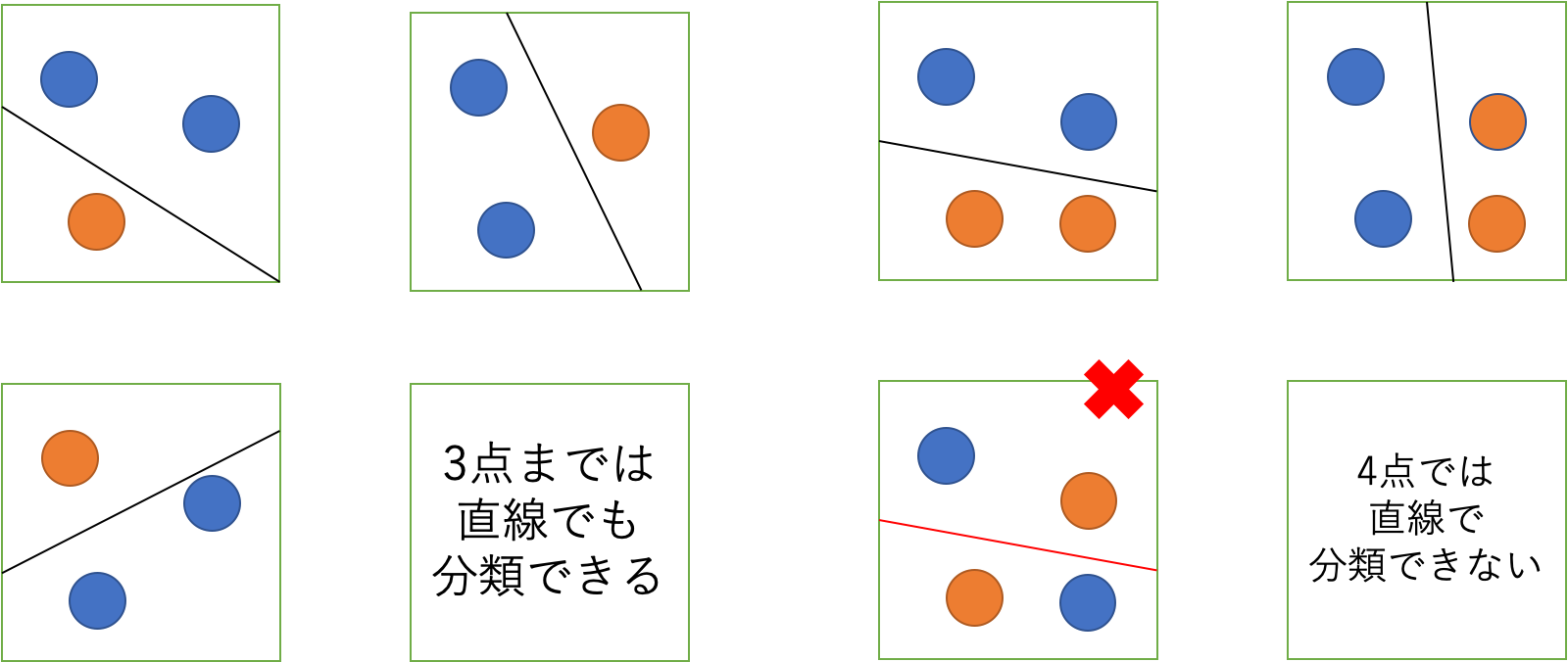
この図の場合次のような結論になります。
2次元空間における線形識別器(直線)のVC次元は3次元
「ディープラーニングと物理学」では次のように書いてありました。
モデル$Q_J$を$$Q_J(x, d) = Q_J(d \mid x)P(x) = \delta(f_J(x) - d) P(x)$$とします。
$\delta(•)$はDiracのデルタ関数です。
以下の議論は簡単のため$d \in \{0, 1\}$の二値分類問題とします。
この時、$f_J (x)$は入力$x$を$0, 1$に振り分ける仕事をしており、その振り分け方の総数はデータ数を$N$とすると$2^N$通りあります。もし$J$を十分動かして$$[f_J(x_1), f_J(x_2), \ldots, f_J(x_N)]$$がその全ての振り分け方を実現できるなら、モデル$Q_J$はデータに対して完全学習できる能力があることになります。
このような状況が実現される$N$の最大値をVC次元と言います。
先の線形識別器の場合ではデータ数$3$までは全ての振り分け方を実現できるため、「VC次元は3次元である」という結論になりますね。
過学習と汎化の難しさ
さて、色々と議論をすっ飛ばして汎化誤差と経験誤差の不等式を示します。というか導出過程が調べてもいまいち見つからなかった/実は見つかってるけど理解できず気付いてないので途中を書けませんでした...
この本が「ディープラーニングと物理学」で参考文献として示されていました。高いので買えません。笑
閑話休題...
不等式を示します。
D_{KL}(P \| Q_J) \le D_{KL}(\hat{P} \| Q_J) + \mathcal{O}\left( \sqrt{\cfrac{\log{\frac{N}{d_{VC}}}}{\frac{N}{d_{VC}}}} \right)
$\mathcal{O}(•)$はランダウの記法で表された計算オーダです。$N$はデータ数、$d_{VC}$がVC次元です。
まず、とりあえず私たちが学習の指標として使える経験誤差$D_{KL}(\hat{P} \| Q_J)$を小さくすることを考えましょう。これを小さくするためにできることは以下の二つがまず考えられます。
- パラメータ$J$を調整する
- モデルの表現力を向上させる
一つ目に関しては、ニューラルネットワークにおいては誤差逆伝播法と勾配降下法を用いることで実現されています。ただこれだけではもちろん限界があるので、モデルの表現力を向上させる必要があります。
ニューラルネットワークにおけるモデルの表現力向上は各層のニューロンの数を増やすことか層を深くすることで実現されます。
そのような形でモデルを複雑化していけば、原理的には経験誤差を限りなく小さくすることも可能でしょう。
一方で
表現力を向上させる$=$仮説を高次元化する
と言い換えることができます。例えば2次元の特徴空間を識別するために、2次元の関数を用いるのではなく3次元の関数を用いるイメージです。
高次元化するとモデルの表現力は飛躍的に向上します。ただし$d_{VC}$次元も伴って。
これが意味するところは、データ数に対してあまりに高次元化しすぎると$$\cfrac{N}{d_{VC}} \to 0$$となる、つまるところ
\lim_{\frac{N}{d_{VC}} \to 0} \cfrac{\log \frac{N}{d_{VC}}}{\frac{N}{d_{VC}}} = \infty \\
\Leftrightarrow D_{KL}(P \| Q_J) \le D_{KL}(\hat{P} \| Q_J) + \infty
となってしまうわけです。これでは経験誤差をいくら小さくしても汎化誤差を小さくしたと保証することができません。流石に無限大まで発散、というのは現実的ではないですが、こんな感じで汎化誤差を小さくしたことを保証できない状態を過学習といいます。
したがって、データのスケールに応じて適切なモデルを用意しないといけません。この考え方をオッカムの剃刀とか言ったりもします。
さて、既存研究が提案しているResNetなどのモデルは圧倒的に複雑です。その分データ数に対して圧倒的に巨大な$d_{VC}$次元となってしまっており、先の不等式では汎化性能が保証できません。しかしながら十分に良い汎化性能を示しているように見えています。
では上記の議論が間違いかというとそうではなく、上記の不等式では保証できないだけで、もしかするともっと詳細な、
D_{KL}(P \| Q_J) \le D_{KL}(\hat{P} \| Q_J) + \mathcal{O}(\textrm{Some formula}) \le D_{KL}(\hat{P} \| Q_J) + \mathcal{O}\left( \sqrt{\cfrac{\log{\frac{N}{d_{VC}}}}{\frac{N}{d_{VC}}}} \right)
と書けるような不等式が存在する可能性があります。そのような不等式を探す試みは色々となされているようですが、2019年1月時点では発見されていないようです。
これが過学習と汎化の難しさですね。
おわりに
もしより詳細な不等式が発見されて、より理論的にニューラルネットワークを構築することができればブラックボックス問題などの解明にも役立ちそうですよね!
参考
- ■S3 群(脳・知能・人間)– 3 編(人工知能と学習)
- 計算論的学習理論入門 -PAC学習とかVC次元とか-
- 統計的学習理論(有限仮説集合の場合の予測損失の上界)
- 統計的学習理論でのコトバの定義が分かりやすかったのでまとめ
-
カルバック・ライブラー距離とも呼ばれています。ちなみに距離の公理を満たしていないため、実際は分離度と呼ばれるものに分類されます。 ↩