BRDFと偏光BRDF(pBRDF)の違い

BRDFとは

BRDF(Bidirectional Reflectance Distribution Function) とは、双方向反射率分布関数を表し、ある特定の角度で光が入射・反射した時、その反射率を返す関数のことです。偏光BRDF(pBRDF)とは、それを偏光も考慮するようにしたものになります。

最新の物理ベースレンダラーMitsuba2では、偏光レンダリングの機能が実装されています。
偏光レンダリングを実施する上では、光の偏光状態を追跡していかなければならず、光が反射・透過した時の偏光状態の変化を計算できなければなりません。その計算をする上で偏光BRDFは必要不可欠なものとなります。
関連記事は以下になります。

• 最新物理ベースレンダラー Mitsuba2を触ってみる(1) 導入編
• 最新物理ベースレンダラー Mitsuba2を触ってみる(4) 偏光レンダリング編

少し学術的な込み入った話になります。
細かいところで私の自己満足的なまとめも含まれているので興味のある方以外は流し読みで良いと思います。
以下の説明はなるべく直観的な理解が出来るよう平易な表現を使うようにしたので、厳密な定義からは外れていることが多くあります。
なるべく出典元の文献へのリンクを貼っていくつもりです。ご容赦下さい。

無偏光BRDF（普通のやつ）

まずpBRDFの詳細を見る前に、従来のBRDFの式について復習をします。
典型的なマイクロファセット（微細表面 ）を考慮した等方性BRDFモデル$f$は下記のような関数で表されます。

f = f_d + f_s = \frac{\rho}{\pi} + k_s\frac{DGF}{4 \cos{\theta_i} \cos{\theta_o}}

もちろんBRDFには他の形のモデル（もっと簡単なものや、もっと複雑なもの）も沢山ありますが、pBRDFで基本形として採用しているのがこの式なので、以降はこの式を通常の無偏光BRDFとします。ちなみにBRDFとしてすべての物質を表現できる完全なモデルはまだ発明されていません（その中でもDisney [Burley2012¹]のモデルは比較的広範囲の物質を再現できますが、複雑です）、なのであくまでも様々な仮定ありきのパラメータ付きモデルとして付き合うのが良いです。

$f_d=\frac{\rho}{\pi}$は拡散反射項、$f_s=k_s\frac{DGF}{4 \cos{\theta_i} \cos{\theta_o}}$は鏡面反射項で、拡散反射（物体本来の色）と鏡面反射（テカリのような成分）2つの足し合わせで表現されます。これをニ色性反射モデルと呼びます、ほとんどのBRDFモデルはニ色性反射を採用しています。
$\rho$は拡散反射の反射率（アルベド）、$k_s$は鏡面反射の反射率（アルベド）、$\theta_i$は入射角、$\theta_o$は出射角になります。
入射ベクトル$\boldsymbol{\rm{\omega}}_i$、出射ベクトル$\boldsymbol{\rm{\omega}}_o$として下図にイメージを描きました。

$\boldsymbol{\rm{h}}$は入射ベクトルと出射ベクトルのハーフベクトルで、下記で計算できます。

\boldsymbol{\rm{h}}=norm(\boldsymbol{\rm{\omega}}_i+\boldsymbol{\rm{\omega}}_o)

$norm$はベクトルの正規化です。このハーフベクトル$\boldsymbol{\rm{h}}$は物理ベースのBRDFを計算するうえで必要不可欠なものになります。

拡散反射項

f_d = \frac{\rho}{\pi}

拡散反射項$f_d=\rho / \pi$は、入射・出射方向に依存せず常に一定なります、これをランバート反射と呼びます。
（完全に脱線しますが、ランバート反射の発見は1760年で永久カメラの発明より約一世紀ほど昔になります、凄いですね）。

鏡面反射項

f_s = k_s\frac{DGF}{4 \cos{\theta_i} \cos{\theta_o}}

マイクロファセット分布項D

$D$はマイクロファセット分布項になります。マイクロファセットとは通常の法線$\boldsymbol{\rm{n}}$では捉えられない無数の表面の微小な形状のことです。
マイクロファセット理論には下図で示すように「鏡面反射を跳ね返すマイクロファセットは、そのマイクロファセットの法線$\boldsymbol{\rm{m}}$とハーフベクトル$\boldsymbol{\rm{h}}$が一致したものだけ」という仮定があります。なのでハーフベクトル$\boldsymbol{\rm{h}}$に対するマイクロファセットの分布（数）がわかれば、確率的にその鏡面反射の程度がわかるということになります。

マイクロファセット分布項$D$だけでも様々なモデルが提案されていますが、最もポピュラーなモデルの１つであるGGXモデル[Walter2007²]は下式で表されます。

D = \frac{\sigma^2}{\pi \cos^4{\theta_h}(\sigma^2+\tan^2{\theta_h})^2}

入射ベクトルと出射ベクトルのハーフベクトル$\boldsymbol{\rm{h}}$を計算し、$\boldsymbol{\rm{h}}$と法線$\boldsymbol{\rm{n}}$の間の角度が$\theta_h$になります。ハーフベクトル$\boldsymbol{\rm{h}}$の角度が$\theta_h$のときのマイクロファセットの数（割合）を得られます。$\theta_h$に従った$D$の値を以下に示します。

$\sigma(>0)$は表面の粗さを表し、大きいほど鏡面反射が反射方向で大きく広がるイメージです、大体の物質は$\sigma<1$で表現できます。$\sigma=1$で一様分布になり、$\sigma>1$でスーパーラフの（表面が非常に粗く、ハーフベクトルの直交方向に強く反射する）物質を表現できます、ただこのような物質は稀です。ほとんどの物質は$\sigma<1$なので、$\theta_h=0$になるとき鏡面反射が最大になります。「表面法線と一致するマイクロファセット法線の数がなんとなく一番多そうだよね」という理解で良いと思います。あくまでもモデルなのですから。

Masking-Shadowing項（幾何減衰項）G

$G$はmasking-shadowing項（幾何減衰項）で、ある方向のマイクロファセット法線を持つマイクロファセットの中でどの程度が遮蔽されているかを返す関数になります。表面に微細な形状があると当然光がそのまま見えない場所も存在しますので、それを考慮する項です。
これも様々なモデルがあるのですが、有名なSmithモデル[Heitz2014³]は下式になります。

G = \Bigg(\frac{2}{1+\sqrt{1+\sigma^2 \tan^2{\theta_i}}}\Bigg)\Bigg(\frac{2}{1+\sqrt{1+\sigma^2 \tan^2{\theta_o}}}\Bigg)

下図で表されるように入射・出射角度が大きくなるほど、遮蔽される割合が上がるので減衰していきます。また表面粗さ$\sigma$が大きくなる（右にいく）ほど、減衰の程度が上がっていきます。これは直観とも合っていますね。

幾何減衰項$G$も物理的な考察を出発点に複雑な計算を伴って導かれているのですが、pBRDFの本質とはあまり絡まないので今回は詳細な説明は省略させていただきます。こちらのサイトさんが非常に詳しいです。

フレネル項F

$F$はフレネル項です。光が屈折率の異なる物質間の界面に入射すると、一部は反射し、一部は透過（屈折）します。この現象を式で表現したものがフレネル式で、通常（無偏光）のBRDFでは反射のみを扱います。フレネルの式は偏光と密接な関係があります、なので通常のBRDFでは無偏光を仮定していますが、偏光の概念を使いなるべく丁寧に説明します。

入射面と垂直に振動する偏光をs偏光、入射面内で振動する偏光をp偏光と呼びます、下図のようにそれぞれの偏光で反射率および透過率が違います。反射率・透過率についてはマクスウェル方程式から出発して電磁場の境界条件を元に導かれます。

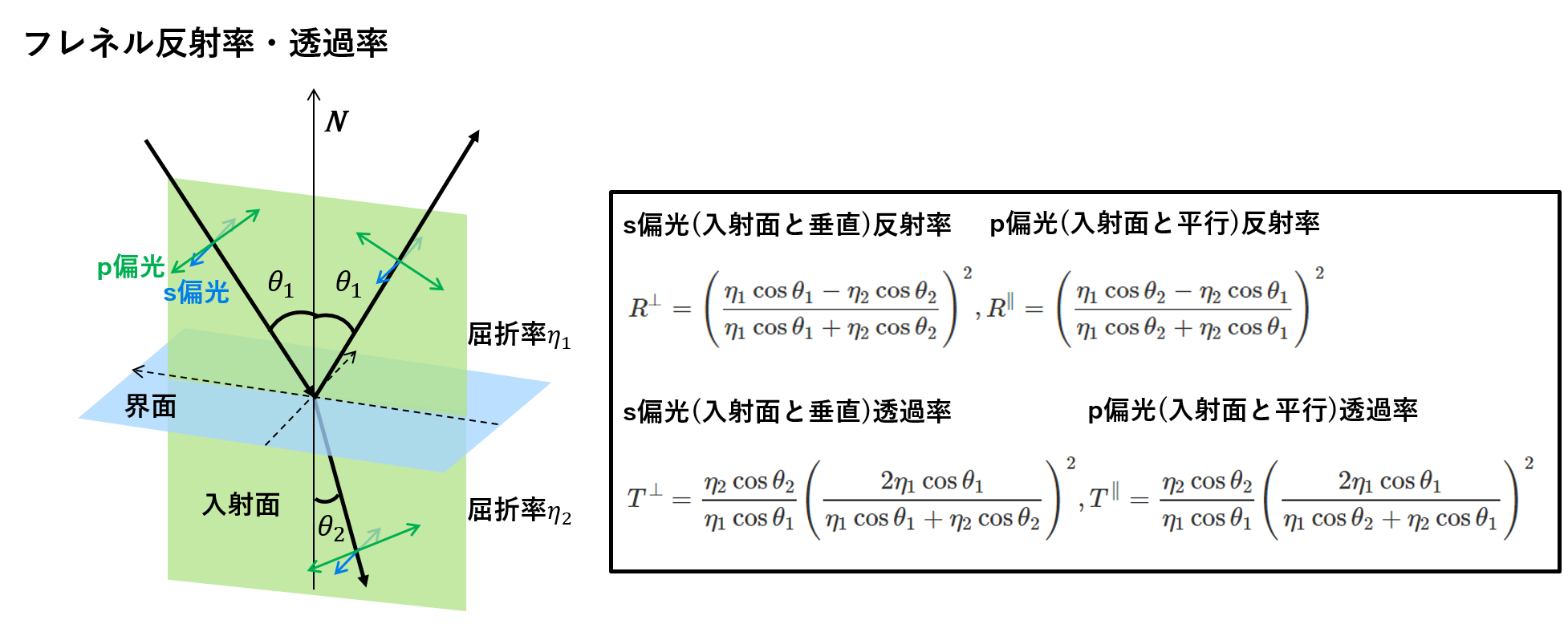
今回は反射のみを扱うので、s偏光のフレネル反射率を$R^\perp$、p偏光のフレネル反射率を$R^\parallel$とすると下式で表されます。

R^\perp = \Bigg(\frac{\eta_1 \cos{\theta_1}-\eta_2 \cos{\theta_2}}{\eta_1 \cos{\theta_1}+\eta_2 \cos{\theta_2}}\Bigg)^2 ,
R^\parallel = \Bigg(\frac{\eta_1 \cos{\theta_2}-\eta_2 \cos{\theta_1}}{\eta_1 \cos{\theta_2}+\eta_2 \cos{\theta_1}}\Bigg)^2

ここで$\theta_1$は入射角、$\theta_2$は屈折角、$\eta_1$は入射側の屈折率、$\eta_2$は反射する物質の屈折率です。
ここでスネルの法則により、下式が成り立ちます。

\frac{\sin \theta_1}{\sin \theta_2} = \frac{\eta_2}{\eta_1}

変形をすると、

\cos{\theta_2}=\sqrt{1-((\eta_1/\eta_2)\sin{\theta_1})^2}

上記を代入すると、

R^\perp = \Bigg(\frac{\eta_1 \cos{\theta_1}-\eta_2 \sqrt{1-((\eta_1/\eta_2)\sin{\theta_1})^2}}{\eta_1 \cos{\theta_1}+\eta_2 \sqrt{1-((\eta_1/\eta_2)\sin{\theta_1})^2}}\Bigg)^2 ,
R^\parallel = \Bigg(\frac{\eta_1 \sqrt{1-((\eta_1/\eta_2)\sin{\theta_1})^2}-\eta_2 \cos{\theta_1}}{\eta_1 \sqrt{1-((\eta_1/\eta_2)\sin{\theta_1})^2}+\eta_2 \cos{\theta_1}}\Bigg)^2

光は空気中からオブジェクトで反射すると仮定すると、$\eta_2/\eta_1=\eta$と空気との相対屈折率で表すことができます。
よって、$\eta_2/\eta_1=\eta$（相対屈折率）とし、$\theta_1=\theta_i$とすると。

R^\perp = \Bigg(\frac{\cos{\theta_i}-\eta \sqrt{1-((1 / \eta)\sin{\theta_i})^2}}{\cos{\theta_i}+\eta \sqrt{1-((1 / \eta)\sin{\theta_i})^2}}\Bigg)^2 ,
R^\parallel = \Bigg(\frac{\sqrt{1-((1 / \eta)\sin{\theta_i})^2}-\eta \cos{\theta_i}}{\sqrt{1-((1 / \eta)\sin{\theta_i})^2}+\eta \cos{\theta_i}}\Bigg)^2

無偏光の場合、フレネル反射率$R$は、s偏光フレネル反射率$R^\perp$とp偏光フレネル反射率$R^\parallel$の平均になります。
またサブサーフェス（一回物質内に入り出射する光）を考慮しないので、フレネル項$F=R$となります。
よってフレネル項$F$は下式で表されます。

F = \frac{1}{2}(R^\perp+R^\parallel)=\frac{1}{2}\Bigg(\frac{\cos{\theta_i}-\eta \sqrt{1-((1 / \eta)\sin{\theta_i})^2}}{\cos{\theta_i}+\eta \sqrt{1-((1 / \eta)\sin{\theta_i})^2}}\Bigg)^2+\frac{1}{2}\Bigg(\frac{\sqrt{1-((1 / \eta)\sin{\theta_i})^2}-\eta \cos{\theta_i}}{\sqrt{1-((1 / \eta)\sin{\theta_i})^2}+\eta \cos{\theta_i}}\Bigg)^2

色々な計算をしているように見えますが、結局のところ入射光の角度$\theta_i$と相対屈折率$\eta$の2変数のみに依存するということになります。入射光の角度$\theta_i$と相対屈折率$\eta$によって、フレネル項$F$（反射率$R$）とs偏光フレネル反射率$R^\perp$とp偏光フレネル反射率$R^\parallel$がどのように変化するか見てみます。一見式が複雑に見えるのでコードも載せます。

import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')

theta = np.arange(90)
eta_list = [1.0, 1.5, 2.0, 2.5]

t = np.radians(theta) # degree -> radian
ct = np.cos(t)

for eta in eta_list:
  st = (1-(1/eta*np.sin(t))**2)**0.5
  Rs = ((ct - eta*st)/(ct + eta*st))**2
  Rp = ((st - eta*ct)/(st + eta*ct))**2
  F = (Rs + Rp)*0.5
  plt.plot(theta, F, '-',label='n={}'.format(eta)) # Change F to Rs, Rp

plt.title('Fresnel term') # Change to Rs, Rp 
plt.legend()
plt.xlabel('theta_i')
plt.xlim(0, 90)
plt.ylim(0, 1)
plt.show()

左から、フレネル項$F$（反射率$R$）、s偏光フレネル反射率$R^\perp$、p偏光フレネル反射率$R^\parallel$と相対屈折率$\eta$を変えながらプロットしています。
フレネル項$F$は入射角$\theta_i$が90°に近くなるに従って急激に上がります。s偏光フレネル反射率$R^\perp$も入射角$\theta_i$に従い増加します。しかしp偏光フレネル反射率$R^\parallel$は入射角$\theta_i$が60°付近になると1回0になり、その後に急激に増加します（このp偏光反射率が0になる角度のことをブリュースター角$\theta_B$と呼び、屈折率$\eta$を使い$\theta_B=\tan^{-1}{\eta}$で求めることができます）。

偏光BRDF

Mitsuba2の偏光レンダリングの解説でも述べたのですが、偏光の状態は4次元のストークスペクトル$\boldsymbol{\rm{s}}=[s_0, s_1, s_2, s_3]$で表現されます。
$s_0$：輝度（振幅）
$s_1$：直線偏光の水平成分(0°)と垂直成分(90°)の差、$s_1=1$は完全水平偏光、$s_1=-1$は完全垂直偏光
$s_2$：直線偏光の45°成分と135°成分の差、$s_2=1$は完全45°偏光、$s_2=-1$は完全135°偏光
$s_3$：円偏光の右回り成分と左回り成分の差、$s_3=1$は完全右回り円偏光、$s_3=-1$は完全左回り円偏光

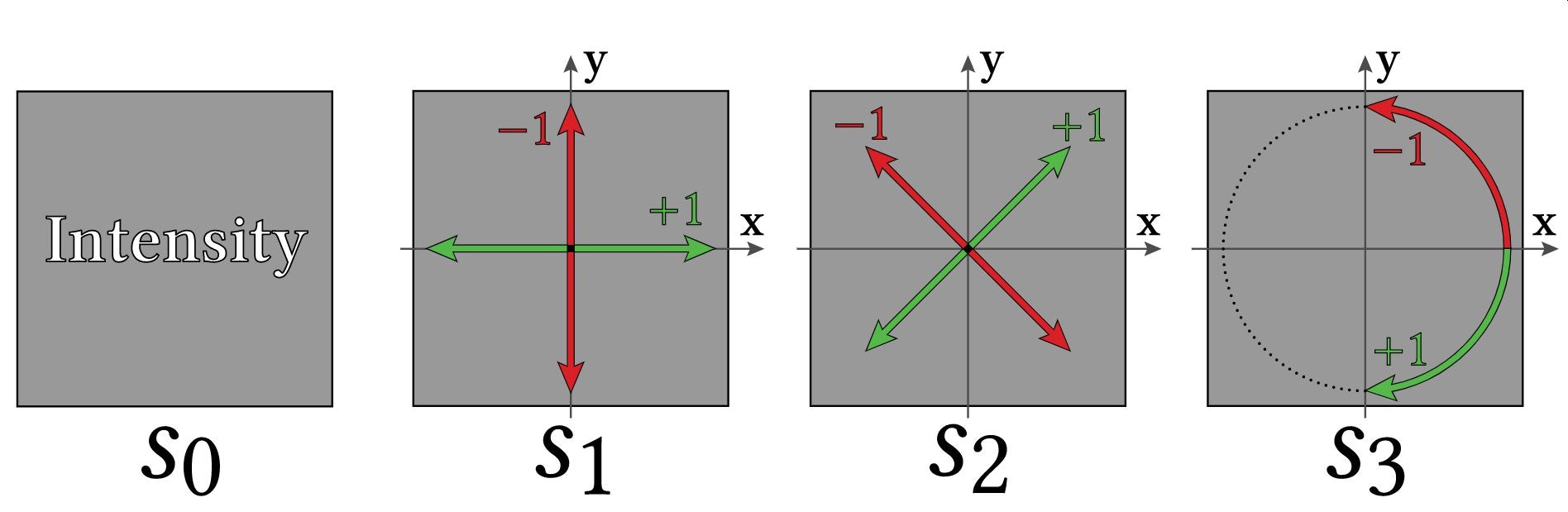
従来のレンダラーでは偏光状態を考慮しない（無偏光）ので、$\boldsymbol{\rm{s}}=[1,0,0,0]$だったことになります。
レンダリング中は、光はオブジェクトと相互作用し、偏光状態が変化します。この変化をミューラー行列$\boldsymbol{\rm{M}} \in \mathbb{R}^{4 \times 4}$で記述します。
光がオブジェクトで反射や透過をするとき、入射光のストークスベクトル$\boldsymbol{\rm{s}}_i$と出射光$\boldsymbol{\rm{s}}_o$のストークスベクトルの関係性は以下になります。

\boldsymbol{\rm{s}}_o = \boldsymbol{\rm{M}} \boldsymbol{\rm{s}}_i

これらを考慮した入射ベクトル$\boldsymbol{\rm{\omega}}_i$、出射ベクトル$\boldsymbol{\rm{\omega}}_o$との関係性は下図になります。

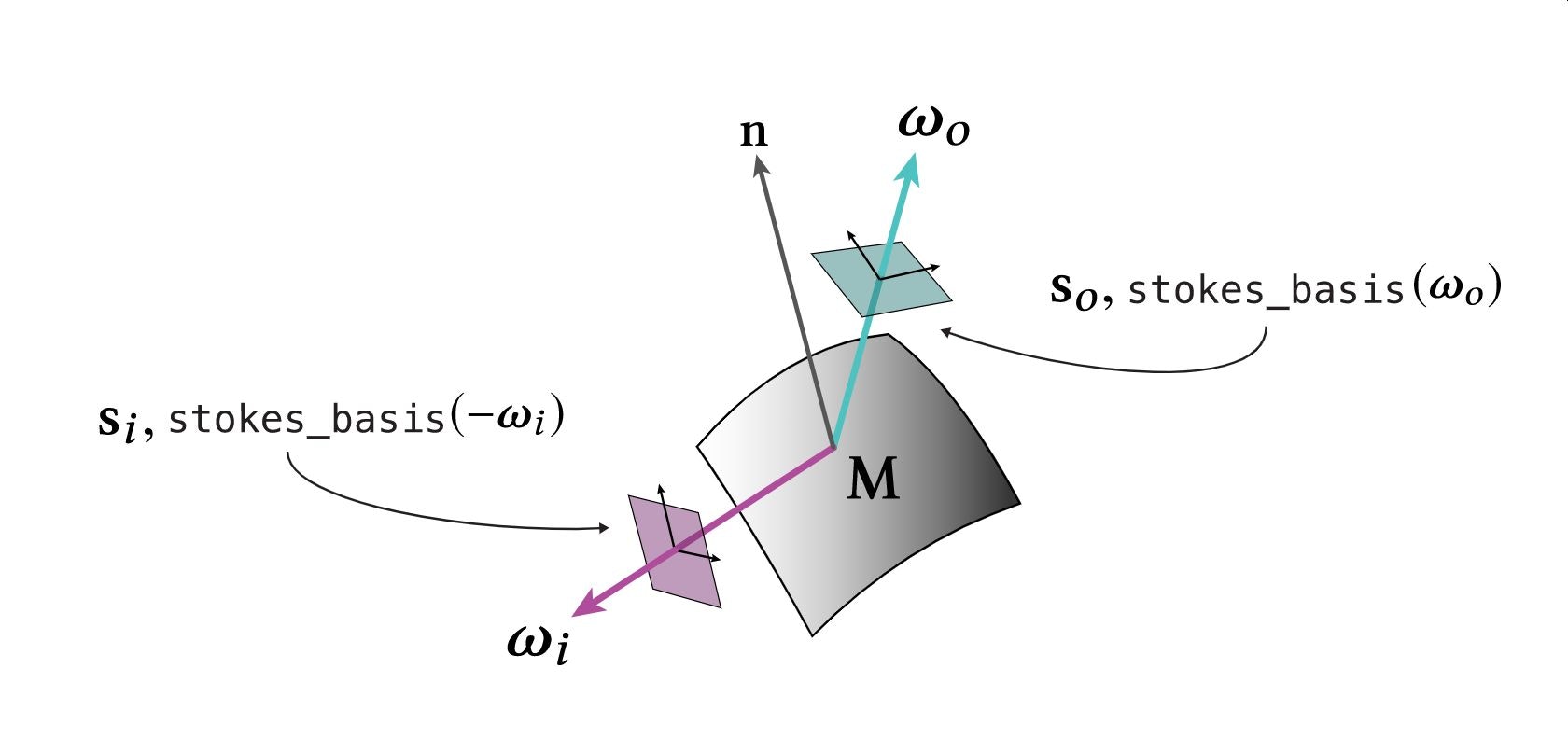
pBRDFも入射・出射ベクトルが求まったらその比（反射率みたいなもの）が求まるのは従来のBRDFと変わっていないです。
ただ従来のBRDFのスカラー値ではなく上記のような$4 \times 4$のミューラー行列を返すようになります。正確にはCosine減衰$\cos \theta_i = (\boldsymbol{\rm{n}} \cdot \boldsymbol{\rm{\omega}}_i)$があるので、偏光BRDF$\boldsymbol{\rm{P}}$を使った場合、下式で入射出射のストークスベクトルの変化を表現できます。

\boldsymbol{\rm{s}}_o = (\boldsymbol{\rm{n}} \cdot \boldsymbol{\rm{\omega}}_i)\boldsymbol{\rm{P}} \boldsymbol{\rm{s}}_i

以降はMitsuba2がpBRDFを実装する上でのベースとなっている[Baek2018⁴]を参考にして解説をしていきます。
偏光BRDF$\boldsymbol{\rm{P}}$は、通常のBRDFと同じように二色性反射モデルになります。ただし全ての項が$4 \times 4$の行列になります。
下式で表されます。

\boldsymbol{\rm{P}} = \boldsymbol{\rm{P}}_{\rm{d}}+\boldsymbol{\rm{P}}_{\rm{s}}

偏光拡散反射項$ \boldsymbol{\rm{P}}_{\rm{d}} $は下式で表されます。

\boldsymbol{\rm{P}}_{\rm{d}}=\boldsymbol{\rm{C}}_{\rm{n} \rightarrow \rm{o}}(\phi_o)\boldsymbol{\rm{F}}_\rm{o}^T(\theta_o;\eta)\boldsymbol{\rm{D}}(\rho)\boldsymbol{\rm{F}}_\rm{i}^T(\theta_i;\eta)\boldsymbol{\rm{C}}_{\rm{i} \rightarrow \rm{n}}(-\phi_i)

これを１つの行列として表すと下式になります。

\boldsymbol{\rm{P}}_{\rm{d}} = \rho
\begin{bmatrix}
\frac{T_o^\perp+T_o^\parallel}{2}\frac{T_i^\perp+T_i^\parallel}{2} & \frac{T_o^\perp+T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \cos{2 \phi_i} & -\frac{T_o^\perp+T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \sin{2 \phi_i} & 0 \\
\frac{T_o^\perp-T_o^\parallel}{2} \frac{T_i^\perp+T_i^\parallel}{2} \cos{2 \phi_o} & \frac{T_o^\perp-T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \cos{2 \phi_o} \cos{2 \phi_i} & -\frac{T_o^\perp-T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \cos{2 \phi_o} \sin{2 \phi_i} & 0 \\
-\frac{T_o^\perp-T_o^\parallel}{2} \frac{T_i^\perp+T_i^\parallel}{2} \sin{2 \phi_o}& -\frac{T_o^\perp-T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \sin{2 \phi_o} \cos{2 \phi_i} & \frac{T_o^\perp-T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \sin{2 \phi_o} \sin{2 \phi_i} & 0 \\
0 & 0 & 0 & 0
\end{bmatrix}

偏光鏡面反射項$ \boldsymbol{\rm{P}}_{\rm{s}} $は下式で表されます。

\boldsymbol{\rm{P}}_{\rm{s}}=\Bigg(k_s\frac{DG}{4 \cos{\theta_i} \cos{\theta_o}}\Bigg)\boldsymbol{\rm{C}}_{\rm{h} \rightarrow \rm{o}}(\varphi_o)\boldsymbol{\rm{F}}^R(\theta_d;\eta)\boldsymbol{\rm{C}}_{\rm{i} \rightarrow \rm{h}}(-\varphi_i)

これを１つの行列として表すと下式になります。

\boldsymbol{\rm{P}}_{\rm{s}}=\boldsymbol{\rm{P}}_{\rm{s}}=k_s\frac{DG}{4 \cos{\theta_i} \cos{\theta_o}}
\begin{bmatrix}
 \frac{R^\perp+R^\parallel}{2} &
 \frac{R^\perp-R^\parallel}{2}\cos{2 \varphi_i} &
 -\frac{R^\perp-R^\parallel}{2}\sin{2 \varphi_i} &
 0
 \\
 \frac{R^\perp-R^\parallel}{2}\cos{2 \varphi_o} &
 \frac{R^\perp+R^\parallel}{2}\cos{2 \varphi_i}\cos{2 \varphi_o} +\sqrt{R^\perp R^\parallel} \sin{2 \varphi_i}\sin{2 \varphi_o} \cos \delta &
 -\frac{R^\perp+R^\parallel}{2}\sin{2 \varphi_i}\cos{2 \varphi_o} + \sqrt{R^\perp R^\parallel} \cos{2 \varphi_i}\sin{2 \varphi_o} \cos \delta &
 \sqrt{R^\perp R^\parallel}  \sin{2 \varphi_o} \sin \delta
\\
 -\frac{R^\perp-R^\parallel}{2}\sin{2 \varphi_o} &
 -\frac{R^\perp+R^\parallel}{2}\cos{2 \varphi_i}\sin{2 \varphi_o} +\sqrt{R^\perp R^\parallel} \sin{2 \varphi_i}\cos{2 \varphi_o} \cos \delta &
 \frac{R^\perp+R^\parallel}{2}\sin{2 \varphi_i}\sin{2 \varphi_o} + \sqrt{R^\perp R^\parallel} \cos{2 \varphi_i}\cos{2 \varphi_o} \cos \delta &
 \sqrt{R^\perp R^\parallel}  \cos{2 \varphi_o} \sin \delta
\\
 0 &
 -\sqrt{R^\perp R^\parallel} \sin{2 \varphi_i} \sin \delta &
 -\sqrt{R^\perp R^\parallel} \cos{2 \varphi_i} \sin \delta &
 \sqrt{R^\perp R^\parallel} \cos \delta
\end{bmatrix}

拡散反射(Diffuse Reflection)と鏡面反射(Specular Reflection)のイメージは下図です。

偏光の拡散反射項では、偏光した光が1回物質の中に入って、無偏光化されたのちに、物体界面で部分偏光して出射します。
一方偏光の鏡面反射項では、偏光した光が物体界面マイクロファセットの影響を受けて振幅が変わり、偏光したまま反射します。

偏光拡散反射項

\boldsymbol{\rm{P}}_{\rm{d}}=\boldsymbol{\rm{C}}_{\rm{n} \rightarrow \rm{o}}(\phi_o)\boldsymbol{\rm{F}}_\rm{o}^T(\theta_o;\eta)\boldsymbol{\rm{D}}(\rho)\boldsymbol{\rm{F}}_\rm{i}^T(\theta_i;\eta)\boldsymbol{\rm{C}}_{\rm{i} \rightarrow \rm{n}}(-\phi_i)

無偏光BRDFの拡散反射項$\rho / \pi$と比較して、非常に複雑になっているように見えますが、１つ１つ意味を理解していきます。
$\theta_i,\theta_o$は、入射・出射光線と法線ベクトルの間の角度になります。入射・出射角（まとめて天頂角）と呼びます。
$\phi_i, \phi_o$は入射・出射光線の基準座標と法線$\boldsymbol{\rm{n}}$を基準(y軸)とした座標系の間の角度ずれになります、方位角と呼びます。

偏光座標回転行列C

$\boldsymbol{\rm{C}}(\vartheta)$は偏光成分の座標回転ミューラー行列になります。
座標回転ミューラー行列$\boldsymbol{\rm{C}}$は、ストークスベクトルをz軸（光の伝播方向）に対して反時計回りの角度$\vartheta$で回転させます。回転行列は主にストークベクトルの座標系を、適用するミューラー変換行列の座標系に変換するために用いられます。

\boldsymbol{\rm{C}}(\vartheta)=
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & \cos{2\vartheta} & \sin{2\vartheta}  & 0 \\
0 & -\sin{2\vartheta} & \cos{2\vartheta} & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}

$\boldsymbol{\rm C}_{\rm i \rightarrow \rm o}$は入射光の偏光座標系から、入射面の偏光座標系への変換行列になります。

対して$\boldsymbol{\rm C}_{\rm o \rightarrow \rm i}$は出射面の偏光座標系から、カメラ偏光座標系への変換行列です。

偏光フレネル行列F

$\boldsymbol{\rm{F}}(\theta_o;\eta)$はフレネル行列になります。
フレネル行列$\boldsymbol{\rm{F}}$は、反射する場合$\boldsymbol{\rm{F}}^R$、透過する場合$\boldsymbol{\rm{F}}^T$で一般化することができ、下式で表されます。

\boldsymbol{\rm{F}}^{F \in {T, R}}(\theta;\eta)=
\begin{bmatrix}
\frac{F^\perp+F^\parallel}{2} & \frac{F^\perp-F^\parallel}{2} & 0 & 0 \\
\frac{F^\perp-F^\parallel}{2} & \frac{F^\perp+F^\parallel}{2} & 0 & 0 \\
0 & 0 & \sqrt{F^\perp F^\parallel} \cos \delta & \sqrt{F^\perp F^\parallel} \sin \delta \\
0 & 0 & -\sqrt{F^\perp F^\parallel} \sin \delta & \sqrt{F^\perp F^\parallel} \cos \delta
\end{bmatrix}

ここで$\delta$は偏光の垂直成分と平行成分の間の位相遅延です。誘電体表面の場合、下式で表されます。

\delta = \left\{
\begin{array}{ll}
0 & (\theta \leq \theta_B) \\
\pi & (\theta > \theta_B)
\end{array}
\right.

偏光の拡散反射項では、偏光した光が1回物質の中に入り出射します。なのでフレネル透過率を考慮します。フレネル透過率は無偏光BRDFのところでも一瞬触れたのですが、下式で表されます。

T^\perp = \frac{\eta_2 \cos{\theta_2}}{\eta_1 \cos{\theta_1}}\Bigg(\frac{2 \eta_1 \cos{\theta_1}}{\eta_1 \cos{\theta_1}+\eta_2 \cos{\theta_2}}\Bigg)^2 ,
T^\parallel = \frac{\eta_2 \cos{\theta_2}}{\eta_1 \cos{\theta_1}}\Bigg(\frac{2 \eta_1 \cos{\theta_1}}{\eta_1 \cos{\theta_2}+\eta_2 \cos{\theta_1}}\Bigg)^2

ここでフレネル反射率と同じようにスネルの法則$\cos \theta_2=\sqrt{1-((\eta_1/\eta_2)\sin \theta_1)^2}$と相対屈折率$\eta_2/\eta_1=\eta$および$\theta_1=\theta_{i,o}$を代入すると、

T^\perp = \frac{\eta \sqrt{1-((1/\eta)\sin \theta_{i,o})^2}}{\cos{\theta_{i,o}}}\Bigg(\frac{2 \cos{\theta_{i,o}}}{\cos{\theta_{i,o}}+\eta \sqrt{1-((1/\eta)\sin \theta_{i,o})^2}}\Bigg)^2
\\
T^\parallel = \frac{\eta \sqrt{1-((1/\eta)\sin \theta_{i,o})^2}}{\cos{\theta_{i,o}}}\Bigg(\frac{2 \cos{\theta_{i,o}}}{ \sqrt{1-((1/\eta)\sin \theta_{i,o})^2}+\eta \cos{\theta_{i,o}}}\Bigg)^2

この式は更に下記のように整理できます。

T^\perp = \frac{4 \eta \cos{\theta_{i,o}} \sqrt{1-((1/\eta)\sin \theta_{i,o})^2}}{
\bigl(\cos{\theta_{i,o}}+\eta \sqrt{1-((1/\eta)\sin \theta_{i,o})^2}\bigr)^2}
\\
T^\parallel = \frac{4 \eta \cos{\theta_{i,o}} \sqrt{1-((1/\eta)\sin \theta_{i,o})^2}}{ \bigl(\sqrt{1-((1/\eta)\sin \theta_{i,o})^2}+\eta \cos{\theta_{i,o}}\bigl)^2}

$\eta$に対して更に整理できますが、ここで止めます。個人的な好みもあるのですが、この形にしておくことで前のフレネル反射率の計算コードがほぼそのまま流用できます。

左から、フレネル透過率$F^T=(T^\perp+T^\perp)/2$、s偏光フレネル透過率$T^\perp$、p偏光フレネル透過率$T^\parallel$と相対屈折率を変えながらプロットしています。基本的にフレネル反射率と反対の傾向があります。

無偏光化行列D

対象物の表面で吸収された光は、表面下散乱により完全に無偏光化されます。拡散における吸収は$4 \times 4$の無偏光化行列$D$として定式化されます。

\boldsymbol{\rm{D}}(\rho)=
\begin{bmatrix}
\rho & 0 & 0 & 0 \\
0 & 0 & 0 & 0  \\
0 & 0 & 0 & 0  \\
0 & 0 & 0 & 0 
\end{bmatrix}

左上の要素は拡散アルベド$\rho$であり、残りの要素はゼロです。
この行列を通すと、ストークスベクトルの$s_0$以外の成分はゼロになります。

偏光拡散反射項の計算

\boldsymbol{\rm{P}}_{\rm{d}}=\boldsymbol{\rm{C}}_{\rm{n} \rightarrow \rm{o}}(\phi_o)\boldsymbol{\rm{F}}_\rm{o}^T(\theta_o;\eta)\boldsymbol{\rm{D}}(\rho)\boldsymbol{\rm{F}}_\rm{i}^T(\theta_i;\eta)\boldsymbol{\rm{C}}_{\rm{i} \rightarrow \rm{n}}(-\phi_i)

上の行列式を、前述した各ミューラー行列を代入して、計算していきます。

\boldsymbol{\rm{C}}_{\rm{n} \rightarrow \rm{o}}(\phi_o)\boldsymbol{\rm{F}}_\rm{o}^T(\theta_o;\eta)=
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & \cos{2 \phi_o} & \sin{2 \phi_o}  & 0 \\
0 & -\sin{2 \phi_o} & \cos{2 \phi_o} & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\frac{T_o^\perp+T_o^\parallel}{2} & \frac{T_o^\perp-T_o^\parallel}{2} & 0 & 0 \\
\frac{T_o^\perp-T_o^\parallel}{2} & \frac{T_o^\perp+T_o^\parallel}{2} & 0 & 0 \\
0 & 0 & \sqrt{T_o^\perp T_o^\parallel} \cos \delta & \sqrt{T_o^\perp T_o^\parallel} \sin \delta \\
0 & 0 & -\sqrt{T_o^\perp T_o^\parallel} \sin \delta & \sqrt{T_o^\perp T_o^\parallel} \cos \delta
\end{bmatrix}
=
\begin{bmatrix}
\frac{T_o^\perp+T_o^\parallel}{2} & \frac{T_o^\perp-T_o^\parallel}{2} & 0 & 0 \\
\frac{T_o^\perp-T_o^\parallel}{2} \cos{2 \phi_o}& \frac{T_o^\perp+T_o^\parallel}{2} \cos{2 \phi_o}& \sqrt{T_o^\perp T_o^\parallel} \sin{2 \phi_o} \cos \delta & \sqrt{T_o^\perp T_o^\parallel} \sin{2 \phi_o} \sin \delta \\
-\frac{T_o^\perp-T_o^\parallel}{2} \sin{2 \phi_o}& -\frac{T_o^\perp+T_o^\parallel}{2} \sin{2 \phi_o}& \sqrt{T_o^\perp T_o^\parallel} \cos{2 \phi_o} \cos \delta & \sqrt{T_o^\perp T_o^\parallel} \sin{2 \phi_o} \cos\delta \\
0 & 0 & -\sqrt{T_o^\perp T_o^\parallel} \sin \delta & \sqrt{T_o^\perp T_o^\parallel} \cos \delta
\end{bmatrix}

\boldsymbol{\rm{C}}_{\rm{n} \rightarrow \rm{o}}(\phi_o)\boldsymbol{\rm{F}}_\rm{o}^T(\theta_o;\eta)\boldsymbol{\rm{D}}(\rho)=
\begin{bmatrix}
\frac{T_o^\perp+T_o^\parallel}{2} & \frac{T_o^\perp-T_o^\parallel}{2} & 0 & 0 \\
\frac{T_o^\perp-T_o^\parallel}{2} \cos{2 \phi_o}& \frac{T_o^\perp+T_o^\parallel}{2} \cos{2 \phi_o}& \sqrt{T_o^\perp T_o^\parallel} \sin{2 \phi_o} \cos \delta & \sqrt{T_o^\perp T_o^\parallel} \sin{2 \phi_o} \sin \delta \\
-\frac{T_o^\perp-T_o^\parallel}{2} \sin{2 \phi_o}& -\frac{T_o^\perp+T_o^\parallel}{2} \sin{2 \phi_o}& \sqrt{T_o^\perp T_o^\parallel} \cos{2 \phi_o} \cos \delta & \sqrt{T_o^\perp T_o^\parallel} \sin{2 \phi_o} \cos\delta \\
0 & 0 & -\sqrt{T_o^\perp T_o^\parallel} \sin \delta & \sqrt{T_o^\perp T_o^\parallel} \cos \delta
\end{bmatrix}
\begin{bmatrix}
\rho & 0 & 0 & 0 \\
0 & 0 & 0 & 0  \\
0 & 0 & 0 & 0  \\
0 & 0 & 0 & 0 
\end{bmatrix}
=
\begin{bmatrix}
\rho \frac{T_o^\perp+T_o^\parallel}{2}& 0 & 0 & 0 \\
\rho \frac{T_o^\perp-T_o^\parallel}{2} \cos{2 \phi_o}& 0 & 0 & 0  \\
-\rho \frac{T_o^\perp-T_o^\parallel}{2} \sin{2 \phi_o}& 0 & 0 & 0  \\
0 & 0 & 0 & 0 
\end{bmatrix}

\boldsymbol{\rm{C}}_{\rm{n} \rightarrow \rm{o}}(\phi_o)\boldsymbol{\rm{F}}_\rm{o}^T(\theta_o;\eta)\boldsymbol{\rm{D}}(\rho)\boldsymbol{\rm{F}}_\rm{i}^T(\theta_i;\eta)=\rho 
\begin{bmatrix}
\frac{T_o^\perp+T_o^\parallel}{2}& 0 & 0 & 0 \\
\frac{T_o^\perp-T_o^\parallel}{2} \cos{2 \phi_o}& 0 & 0 & 0  \\
-\frac{T_o^\perp-T_o^\parallel}{2} \sin{2 \phi_o}& 0 & 0 & 0  \\
0 & 0 & 0 & 0 
\end{bmatrix}
\begin{bmatrix}
\frac{T_i^\perp+T_i^\parallel}{2} & \frac{T_i^\perp-T_i^\parallel}{2} & 0 & 0 \\
\frac{T_i^\perp-T_i^\parallel}{2} & \frac{T_i^\perp+T_i^\parallel}{2} & 0 & 0 \\
0 & 0 & \sqrt{T_i^\perp T_i^\parallel} \cos \delta & \sqrt{T_i^\perp T_i^\parallel} \sin \delta \\
0 & 0 & -\sqrt{T_i^\perp T_i^\parallel} \sin \delta & \sqrt{T_i^\perp T_i^\parallel} \cos \delta
\end{bmatrix}=\rho 
\begin{bmatrix}
\frac{T_o^\perp+T_o^\parallel}{2}\frac{T_i^\perp+T_i^\parallel}{2} & \frac{T_o^\perp+T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} & 0 & 0 \\
\frac{T_o^\perp-T_o^\parallel}{2} \frac{T_i^\perp+T_i^\parallel}{2} \cos{2 \phi_o}& \frac{T_o^\perp-T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \cos{2 \phi_o} & 0 & 0 \\
-\frac{T_o^\perp-T_o^\parallel}{2} \frac{T_i^\perp+T_i^\parallel}{2} \sin{2 \phi_o}& -\frac{T_o^\perp-T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \sin{2 \phi_o} & 0 & 0 \\
0 & 0 & 0 & 0
\end{bmatrix}

\boldsymbol{\rm{C}}_{\rm{n} \rightarrow \rm{o}}(\phi_o)\boldsymbol{\rm{F}}_\rm{o}^T(\theta_o;\eta)\boldsymbol{\rm{D}}(\rho)\boldsymbol{\rm{F}}_\rm{i}^T(\theta_i;\eta)\boldsymbol{\rm{C}}_{\rm{i} \rightarrow \rm{n}}(-\phi_i)
= \rho
\begin{bmatrix}
\frac{T_o^\perp+T_o^\parallel}{2}\frac{T_i^\perp+T_i^\parallel}{2} & \frac{T_o^\perp+T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} & 0 & 0 \\
\frac{T_o^\perp-T_o^\parallel}{2} \frac{T_i^\perp+T_i^\parallel}{2} \cos{2 \phi_o}& \frac{T_o^\perp-T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \cos{2 \phi_o} & 0 & 0 \\
-\frac{T_o^\perp-T_o^\parallel}{2} \frac{T_i^\perp+T_i^\parallel}{2} \sin{2 \phi_o}& -\frac{T_o^\perp-T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \sin{2 \phi_o} & 0 & 0 \\
0 & 0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & \cos{2 \phi_i} & -\sin{2 \phi_i}  & 0 \\
0 & \sin{2 \phi_i} & \cos{2 \phi_i} & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
= \rho
\begin{bmatrix}
\frac{T_o^\perp+T_o^\parallel}{2}\frac{T_i^\perp+T_i^\parallel}{2} & \frac{T_o^\perp+T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \cos{2 \phi_i} & -\frac{T_o^\perp+T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \sin{2 \phi_i} & 0 \\
\frac{T_o^\perp-T_o^\parallel}{2} \frac{T_i^\perp+T_i^\parallel}{2} \cos{2 \phi_o} & \frac{T_o^\perp-T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \cos{2 \phi_o} \cos{2 \phi_i} & -\frac{T_o^\perp-T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \cos{2 \phi_o} \sin{2 \phi_i} & 0 \\
-\frac{T_o^\perp-T_o^\parallel}{2} \frac{T_i^\perp+T_i^\parallel}{2} \sin{2 \phi_o}& -\frac{T_o^\perp-T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \sin{2 \phi_o} \cos{2 \phi_i} & \frac{T_o^\perp-T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \sin{2 \phi_o} \sin{2 \phi_i} & 0 \\
0 & 0 & 0 & 0
\end{bmatrix}

よって、最終的に下式の偏光拡散反射ミューラー行列が得られます。

\boldsymbol{\rm{P}}_{\rm{d}} = \rho
\begin{bmatrix}
\frac{T_o^\perp+T_o^\parallel}{2}\frac{T_i^\perp+T_i^\parallel}{2} & \frac{T_o^\perp+T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \cos{2 \phi_i} & -\frac{T_o^\perp+T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \sin{2 \phi_i} & 0 \\
\frac{T_o^\perp-T_o^\parallel}{2} \frac{T_i^\perp+T_i^\parallel}{2} \cos{2 \phi_o} & \frac{T_o^\perp-T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \cos{2 \phi_o} \cos{2 \phi_i} & -\frac{T_o^\perp-T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \cos{2 \phi_o} \sin{2 \phi_i} & 0 \\
-\frac{T_o^\perp-T_o^\parallel}{2} \frac{T_i^\perp+T_i^\parallel}{2} \sin{2 \phi_o}& -\frac{T_o^\perp-T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \sin{2 \phi_o} \cos{2 \phi_i} & \frac{T_o^\perp-T_o^\parallel}{2}\frac{T_i^\perp-T_i^\parallel}{2} \sin{2 \phi_o} \sin{2 \phi_i} & 0 \\
0 & 0 & 0 & 0
\end{bmatrix}

偏光鏡面反射項

\boldsymbol{\rm{P}}_{\rm{s}}=\Bigg(k_s\frac{DG}{4 \cos{\theta_i} \cos{\theta_o}}\Bigg)\boldsymbol{\rm{C}}_{\rm{h} \rightarrow \rm{o}}(\varphi_o)\boldsymbol{\rm{F}}^R(\theta_d;\eta)\boldsymbol{\rm{C}}_{\rm{i} \rightarrow \rm{h}}(-\varphi_i)

1回の反射だけを考慮するので行列式だけ見ると偏光拡散反射項と比較してかなりシンプルです。
無偏光BRDFのフレネル項をミューラー行列にしたものと捉えることができます。
$D$はマイクロファセット分布項、$G$はMasking-Shadowing項です。これらは無偏光BRDFで用いているものと同じなので、説明は省略します。

他もほとんど偏光拡散反射項の方と同じミューラー行列なのですが、偏光座標回転行列の解釈の仕方が少し異なります。
無偏光BRDFのところで説明したマイクロファセット理論によれば、鏡面反射はハーフベクトルと一致したマイクロファセットのみで生じると仮定されています。したがって鏡面反射偏光のストークスベクトルは、表面法線$\boldsymbol{\rm{n}}$ ではなくハーフベクトル$\boldsymbol{\rm{h}}$ を基準にして計算されます。必然座標回転行列の基準面もハーフベクトルを用いて構成されます。
$\varphi_i, \varphi_o$は入射・出射光線の基準座標とハーフベクトル$\boldsymbol{\rm{h}}$を基準(y軸)とした座標系の間の角度ずれ（方位角）になります。

偏光鏡面反射項の計算

偏光拡散反射項と同じように、ミューラー行列を順に計算していきます。

\boldsymbol{\rm{C}}_{\rm{h} \rightarrow \rm{o}}(\varphi_o)\boldsymbol{\rm{F}}^R(\theta_d;\eta)=
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & \cos{2 \varphi_o} & \sin{2 \varphi_o}  & 0 \\
0 & -\sin{2 \varphi_o} & \cos{2 \varphi_o} & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\frac{R^\perp+R^\parallel}{2} & \frac{R^\perp-R^\parallel}{2} & 0 & 0 \\
\frac{R^\perp-R^\parallel}{2} & \frac{R^\perp+R^\parallel}{2} & 0 & 0 \\
0 & 0 & \sqrt{R^\perp R^\parallel} \cos \delta & \sqrt{R^\perp R^\parallel} \sin \delta \\
0 & 0 & -\sqrt{R^\perp R^\parallel} \sin \delta & \sqrt{R^\perp R^\parallel} \cos \delta
\end{bmatrix}
=
\begin{bmatrix}
\frac{R^\perp+R^\parallel}{2} & \frac{R^\perp-R^\parallel}{2} & 0 & 0 \\
\frac{R^\perp-R^\parallel}{2}\cos{2 \varphi_o} & \frac{R^\perp+R^\parallel}{2}\cos{2 \varphi_o} & \sqrt{R^\perp R^\parallel} \sin{2 \varphi_o} \cos \delta & \sqrt{R^\perp R^\parallel}  \sin{2 \varphi_o} \sin \delta \\
-\frac{R^\perp-R^\parallel}{2}\sin{2 \varphi_o} & -\frac{R^\perp+R^\parallel}{2}\sin{2 \varphi_o} & \sqrt{R^\perp R^\parallel} \cos{2 \varphi_o} \cos \delta & \sqrt{R^\perp R^\parallel}  \cos{2 \varphi_o} \sin \delta \\
0 & 0 & -\sqrt{R^\perp R^\parallel} \sin \delta & \sqrt{R^\perp R^\parallel} \cos \delta
\end{bmatrix}

\boldsymbol{\rm{C}}_{\rm{h} \rightarrow \rm{o}}(\varphi_o)\boldsymbol{\rm{F}}^R(\theta_d;\eta)\boldsymbol{\rm{C}}_{\rm{i} \rightarrow \rm{h}}(-\varphi_i)=
\begin{bmatrix}
 \frac{R^\perp+R^\parallel}{2} & \frac{R^\perp-R^\parallel}{2} & 0 & 0
 \\
 \frac{R^\perp-R^\parallel}{2}\cos{2 \varphi_o} &
 \frac{R^\perp+R^\parallel}{2}\cos{2 \varphi_o} &
 \sqrt{R^\perp R^\parallel} \sin{2 \varphi_o} \cos \delta &
 \sqrt{R^\perp R^\parallel}  \sin{2 \varphi_o} \sin \delta
 \\
 -\frac{R^\perp-R^\parallel}{2}\sin{2 \varphi_o} &
 -\frac{R^\perp+R^\parallel}{2}\sin{2 \varphi_o} &
 \sqrt{R^\perp R^\parallel} \cos{2 \varphi_o} \cos \delta &
 \sqrt{R^\perp R^\parallel}  \cos{2 \varphi_o} \sin \delta
 \\
 0 &
 0 &
 -\sqrt{R^\perp R^\parallel} \sin \delta &
 \sqrt{R^\perp R^\parallel} \cos \delta
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & \cos{2 \varphi_i} & -\sin{2 \varphi_i}  & 0 \\
0 & \sin{2 \varphi_i} & \cos{2 \varphi_i} & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
=
\begin{bmatrix}
 \frac{R^\perp+R^\parallel}{2} &
 \frac{R^\perp-R^\parallel}{2}\cos{2 \varphi_i} &
 -\frac{R^\perp-R^\parallel}{2}\sin{2 \varphi_i} &
 0
 \\
 \frac{R^\perp-R^\parallel}{2}\cos{2 \varphi_o} &
 \frac{R^\perp+R^\parallel}{2}\cos{2 \varphi_i}\cos{2 \varphi_o} +\sqrt{R^\perp R^\parallel} \sin{2 \varphi_i}\sin{2 \varphi_o} \cos \delta &
 -\frac{R^\perp+R^\parallel}{2}\sin{2 \varphi_i}\cos{2 \varphi_o} + \sqrt{R^\perp R^\parallel} \cos{2 \varphi_i}\sin{2 \varphi_o} \cos \delta &
 \sqrt{R^\perp R^\parallel}  \sin{2 \varphi_o} \sin \delta
\\
 -\frac{R^\perp-R^\parallel}{2}\sin{2 \varphi_o} &
 -\frac{R^\perp+R^\parallel}{2}\cos{2 \varphi_i}\sin{2 \varphi_o} +\sqrt{R^\perp R^\parallel} \sin{2 \varphi_i}\cos{2 \varphi_o} \cos \delta &
 \frac{R^\perp+R^\parallel}{2}\sin{2 \varphi_i}\sin{2 \varphi_o} + \sqrt{R^\perp R^\parallel} \cos{2 \varphi_i}\cos{2 \varphi_o} \cos \delta &
 \sqrt{R^\perp R^\parallel}  \cos{2 \varphi_o} \sin \delta
\\
 0 &
 -\sqrt{R^\perp R^\parallel} \sin{2 \varphi_i} \sin \delta &
 -\sqrt{R^\perp R^\parallel} \cos{2 \varphi_i} \sin \delta &
 \sqrt{R^\perp R^\parallel} \cos \delta
\end{bmatrix}

よって、最終的に下式の偏光鏡面反射ミューラー行列が得られます。

\boldsymbol{\rm{P}}_{\rm{s}}=k_s\frac{DG}{4 \cos{\theta_i} \cos{\theta_o}}
\begin{bmatrix}
 \frac{R^\perp+R^\parallel}{2} &
 \frac{R^\perp-R^\parallel}{2}\cos{2 \varphi_i} &
 -\frac{R^\perp-R^\parallel}{2}\sin{2 \varphi_i} &
 0
 \\
 \frac{R^\perp-R^\parallel}{2}\cos{2 \varphi_o} &
 \frac{R^\perp+R^\parallel}{2}\cos{2 \varphi_i}\cos{2 \varphi_o} +\sqrt{R^\perp R^\parallel} \sin{2 \varphi_i}\sin{2 \varphi_o} \cos \delta &
 -\frac{R^\perp+R^\parallel}{2}\sin{2 \varphi_i}\cos{2 \varphi_o} + \sqrt{R^\perp R^\parallel} \cos{2 \varphi_i}\sin{2 \varphi_o} \cos \delta &
 \sqrt{R^\perp R^\parallel}  \sin{2 \varphi_o} \sin \delta
\\
 -\frac{R^\perp-R^\parallel}{2}\sin{2 \varphi_o} &
 -\frac{R^\perp+R^\parallel}{2}\cos{2 \varphi_i}\sin{2 \varphi_o} +\sqrt{R^\perp R^\parallel} \sin{2 \varphi_i}\cos{2 \varphi_o} \cos \delta &
 \frac{R^\perp+R^\parallel}{2}\sin{2 \varphi_i}\sin{2 \varphi_o} + \sqrt{R^\perp R^\parallel} \cos{2 \varphi_i}\cos{2 \varphi_o} \cos \delta &
 \sqrt{R^\perp R^\parallel}  \cos{2 \varphi_o} \sin \delta
\\
 0 &
 -\sqrt{R^\perp R^\parallel} \sin{2 \varphi_i} \sin \delta &
 -\sqrt{R^\perp R^\parallel} \cos{2 \varphi_i} \sin \delta &
 \sqrt{R^\perp R^\parallel} \cos \delta
\end{bmatrix}

まとめ

偏光BRDF(pBRDF)について、従来のBRDFと何が違うのか、比較をしながら見てきました。
基本的なマイクロファセット理論はそのままで、ミューラー行列を使い偏光の変化を追うことができるようになっています。

以上です。

---

1. Brent Burley. 2012. Physically-Based Shading at Disney. ACM SIGGRAPH 2012 Course. ↩

2. Bruce Walter et al. 2007. Microfacet models for refraction through rough surfaces. In Eurographics conference on Rendering Techniques. Eurographics Association, 195–206. ↩

3. Eric Heitz. 2014. Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs. J. Comput. Graph. Techn. 3, 2 (2014), 48–107. ↩

4. Seung-Hwan Baek et al. 2018. Simultaneous Acquisition of Polarimetric SVBRDF and Normals. ACM SIGGRAPH Asia 2018. ↩