はじめに
こんちには。kumiskyです。
R Advent Calendar 2014の31日目の記事です。
お客様にアンケートを実施している企業は多いですよね。
この記事では、アンケート結果の回答同士の関係を見たい時には、どんな手法が適しているだろうか、というお話をしてみたいと思います。
動機
私の勤務先でも顧客満足度調査というアンケートを毎年実施しています。
顧客満足度の目標値があり、それを上げるために行っています。
アンケートでは、総合の満足度と、各要素の満足度をお聞きします。
各要素というのは、機能・デザイン・買いやすさ・窓口の対応などです。
この回答から、製品やサービスのどこに不満を感じると全体の満足度が下がりやすいのか、
今後のお付き合いを止めたいと思うのか、を調べていきます。
顧客に満足してもらうためには何を優先的に改善すると良さそうかを把握したい、というのがモチベーションです。
この時、私がまず総合満足度と各要素の満足度の関係を見るために使ったのは、ピアソンの積率相関係数です。
いわゆる普通の相関です。
試行錯誤
そこに、技術者の方から突っ込みが入りました。
「積率相関係数は、値が正規分布に従うことを仮定しています。
満足度という連続尺度で無いものに、積率相関係数を使うのは違和感がありませんか?」
(尺度のおさらい)────────────────────────────────────────
連続尺度:数値で測れるデータ(身長や体重)
→体重 80gは 40kgの人の 2倍の重さ。各値の間隔が等しい。
順序尺度:順序だけに意味がある値(スポーツの1位2位など)
→5段階評価の 「5」は「1」の 5倍という意味ではない。各値の間隔は等しい訳ではない。
名義尺度:名称などの値(男女や都道府県など)
→各値の間に大小関係がない
───────────────────────────────────────────────────────
アンケート回答などの順序尺度であれば連関係数や順位相関を使うべき、という説もあり、
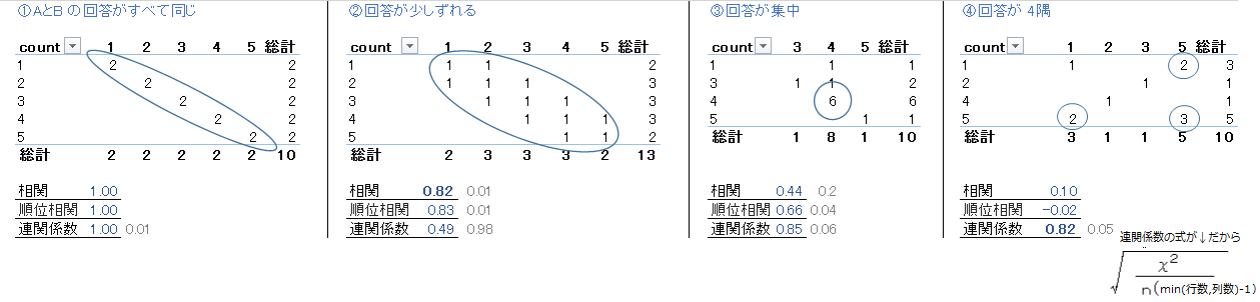
理解のために、まずは 4種類の回答の組み合わせを作って各種相関を出してみました。(サンプルなので回答は 10件だけです)
とても綺麗な線形の関係があるときは、積率相関でも連関係数でも相関が高くなります。(上図の左側)
ただ、例えば点の関係しかない時でも、連関係数だと評価されてしまいます。(上図の右側)
連続尺度でないものに積率相関を使うのはおかしい、という理屈は分かるものの、
こうしてみると、今回のアンケートでは線形の関係を知りたいので、やはり連関係数だと知りたい答えにはたどり着けない気がしてしまいます。
別の相関が登場
そこで、先ほど突っ込みをいただいた技術者に相談してみました。
彼の提案は、ポリコリック相関を使うのはどうか、というものでした。
問題は、連続尺度でないものに積率相関を使うことなので、このケースであれば、回答の方を連続量にしてしまおうという方法です。
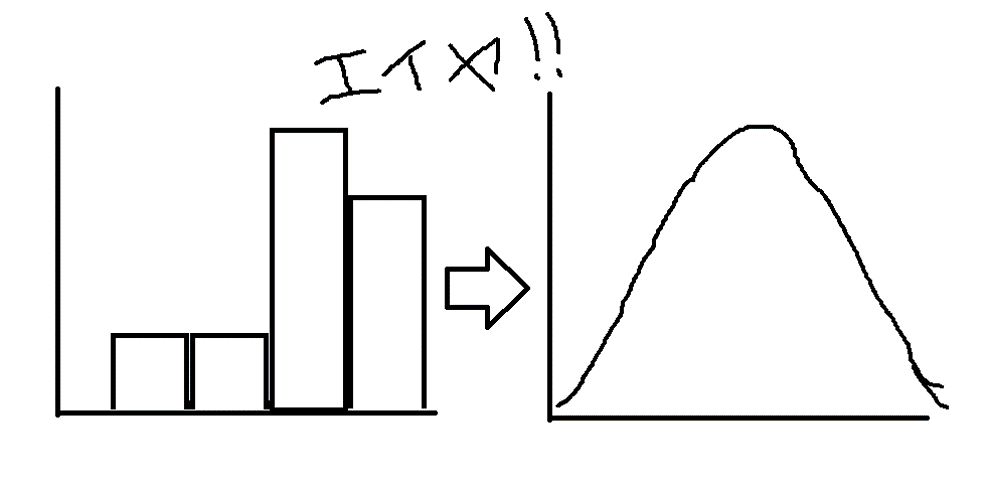
そう、こんな風に、、
と、心理尺度から二次元正規分布になるようなもっともらしい連続量を推定しよう!
そして、その推定した連続量同士の相関を見ればいいじゃないか、というもの。
少し強引な気がするでしょうか。
ポリコリック相関では、アンケート回答など表に出てきている値は順序尺度でも、
回答の裏に隠れた心理量は正規分布しているという仮定をおいています。
順序としては、本当の心理量は下図の右で、回答が下図の左として現れているだけだから、元に戻してから考えよう、という訳です。
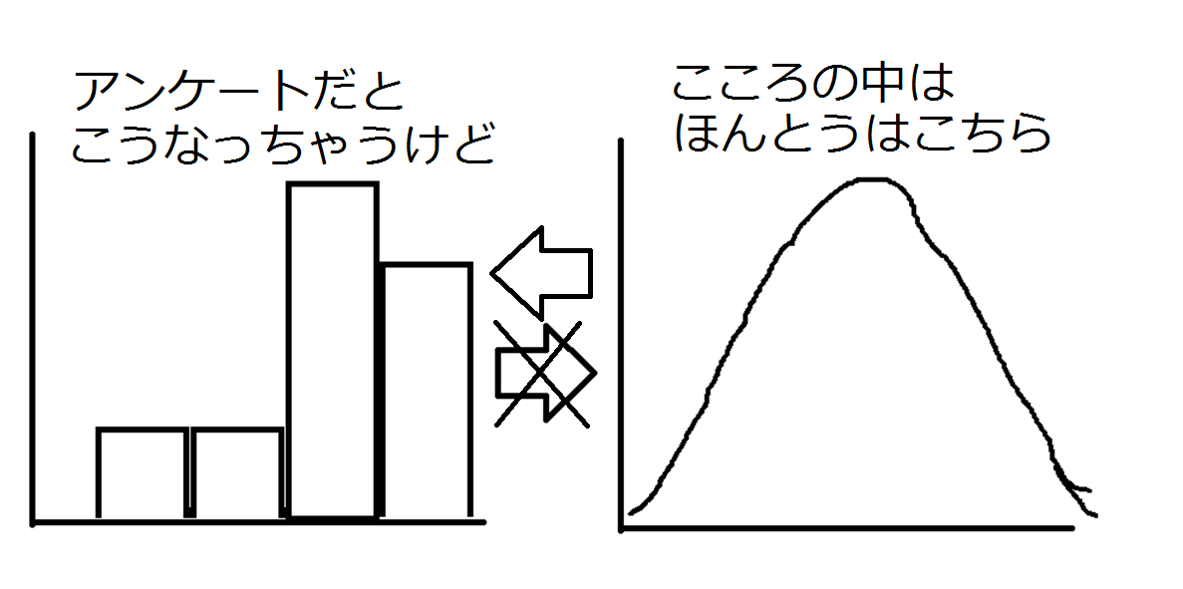
例えば 5点満点中 3点を選択した人の中にも、2点寄りの3点、という人もいれば、4点寄りの3点、という人もいそうですよね。
注意点としては、真値が正規分布を仮定できないような値には使えません。
詳しくは、私の下手な説明よりも以下をご覧ください。
-証明
カテゴリカルデータの相関係数
http://norimune.net/673
-理論
順序尺度の相関係数(ポリコリック相関係数)について (小杉考司)
http://kosugitti.sakura.ne.jp/wp/wp-content/uploads/2013/08/polynote.pdf
私は知りませんでしたが、昔、心理尺度の関係性を見る時にピアソンの相関を使っていたのは妥協の産物だったようで、今はコンピューターの性能が上がり高度な計算もできるようになったので、様々な相関が出てきているようです。
Rのパッケージ
Rでパッケージが提供されてますので、使うときは以下の呪文を唱えるだけで大丈夫です。
ポリコリック相関係数(順序尺度×順序尺度の相関)
install.packages("polycor") # (hなし)
library(polycor)して使う。関数名はpolychor(hあり)
polychor(x,y)
連続尺度×順序尺度の相関を見るポリコリアル相関係数なども提供されています。
polycorパッケージによる順序相関係数の算出
http://www.okada.jp.org/RWiki/?polycor%A5%D1%A5%C3%A5%B1%A1%BC%A5%B8%A4%CB%A4%E8%A4%EB%BD%E7%BD%F8%C1%EA%B4%D8%B7%B8%BF%F4%A4%CE%BB%BB%BD%D0