陰関数でベジェ曲線の交点を求めてみた

はじめに

ベジェ曲線の交点を求める方法は、ベジェ曲線を図形として分割することを繰り返す手法[1][2]のほかに、陰関数を経由して代数方程式に変換し解を求める方法[3][4]もあります。
後者のほうが曲線の形状や交差のパターンの影響を受けずスマートにできそうな気がしますが、試してみると交点は求まるけど実装するのは大変そう ...　という記事です。
（以前投稿した記事の再投稿です）

対象

以下のような2つの3次ベジェ曲線の交点を求めようとします。
　

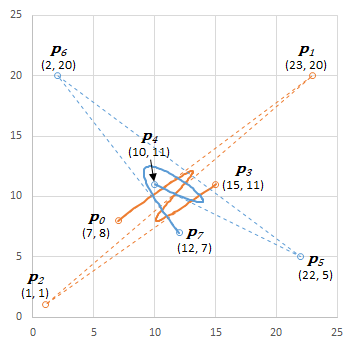
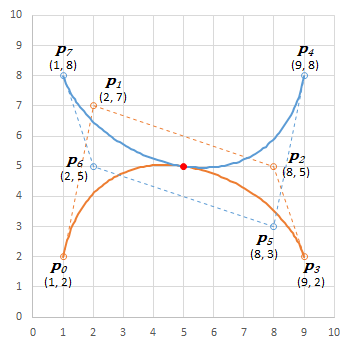
曲線${\boldsymbol{B}}_0$（オレンジ色）は；

\begin{array}{l}
x=f_0(t)=
\begin{bmatrix}
t^3 & t^2 & t & 1
\end{bmatrix}
\begin{bmatrix}
-1 & 3 & -3 & 1 \\
3 & -6 & 3 & 0 \\
-3 & 3 & 0 & 0 \\
1 & 0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
p_{0x} \\
p_{1x} \\
p_{2x} \\
p_{3x}
\end{bmatrix}
=a_0t^3+a_1t^2+a_2t+a_3
\\
y=g_0(t)=
\begin{bmatrix}
t^3 & t^2 & t & 1
\end{bmatrix}
\begin{bmatrix}
-1 & 3 & -3 & 1 \\
3 & -6 & 3 & 0 \\
-3 & 3 & 0 & 0 \\
1 & 0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
p_{0y} \\
p_{1y} \\
p_{2y} \\
p_{3y}
\end{bmatrix}
=b_0t^3+b_1t^2+b_2t+b_3
\end{array}

同様に、曲線${\boldsymbol{B}}_1$（青色）は；

\begin{array}{l}
x=f_1(u)=
\begin{bmatrix}
u^3 & u^2 & u & 1
\end{bmatrix}
\begin{bmatrix}
-1 & 3 & -3 & 1 \\
3 & -6 & 3 & 0 \\
-3 & 3 & 0 & 0 \\
1 & 0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
p_{4x} \\
p_{5x} \\
p_{6x} \\
p_{7x}
\end{bmatrix}
=c_0u^3+c_1u^2+c_2u+c_3
\\
y=g_1(u)=
\begin{bmatrix}
u^3 & u^2 & u & 1
\end{bmatrix}
\begin{bmatrix}
-1 & 3 & -3 & 1 \\
3 & -6 & 3 & 0 \\
-3 & 3 & 0 & 0 \\
1 & 0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
p_{4y} \\
p_{5y} \\
p_{6y} \\
p_{7y}
\end{bmatrix}
=d_0u^3+d_1u^2+d_2u+d_3
\end{array}

とします。$t$と$u$はパラメトリック変数です。

手順

1. $f_0(t)$と$g_0(t)$を陰関数 $F_0(x,y)=0$ に変換する。
2. $F_0(x,y)=0$ の$x$に$f_1(u)$、$y$に$g_1(u)$を代入した$u$についての9次方程式の根を求める。
3. 実数かつ$0$～$1$の根を$f_1(u)$と$g_1(u)$に代入して、交点候補の$x$と$y$を求める。
4. $f_1(u)$と$g_1(u)$を陰関数 $F_1(x,y)=0$ に変換する。
5. $F_1(x,y)=0$ の$x$に$f_0(t)$、$y$に$g_0(t)$を代入した$t$についての9次方程式の根を求める。
6. 実数かつ$0$～$1$の根を$f_0(t)$と$g_0(t)$に代入して、交点候補の$x$と$y$を求める。
7. 交点候補を突き合わせ、ペアになったものが交点。

陰関数に変換

Wolfram AlphaのEliminateで変数$t$を消去し、陰関数に変換できます。[5]

入力

Collect[Expand[Eliminate[{a0*t^3+a1*t^2+a2*t+a3==x,b0*t^3+b1*t^2+b2*t+b3==y},t]],{x,y}]

結果

y (-6 a0^2 a3 b0 b3 + 3 a0^2 a3 b1 b2 - a0 a1 a3 b0 b2 - 2 a0 a1 a3 b1^2 + a0 a2 a3 b0 b1 + 3 a0 a3^2 b0^2 + 2 a1^2 a3 b0 b1 - 3 a1 a2 a3 b0^2) + 3 a0^2 a3 b0 b3^2 + 3 a0^2 a3 b0 y^2 - 3 a0^2 a3 b1 b2 b3 + a0^2 a3 b2^3 + x (6 a0 a3 b0^2 b3 - 6 a0 a3 b0^2 y - 6 a0 a3 b0 b1 b2 + 2 a0 a3 b1^3 + 4 a1 a3 b0^2 b2 - 2 a1 a3 b0 b1^2 + 2 a2 a3 b0^2 b1 - 3 a3^2 b0^3) + a0 a1 a3 b0 b2 b3 + 2 a0 a1 a3 b1^2 b3 - a0 a1 a3 b1 b2^2 - a0 a2 a3 b0 b1 b3 - 2 a0 a2 a3 b0 b2^2 + a0 a2 a3 b1^2 b2 - 3 a0 a3^2 b0^2 b3 + 3 a0 a3^2 b0 b1 b2 - a0 a3^2 b1^3 - 2 a1^2 a3 b0 b1 b3 + a1^2 a3 b0 b2^2 + 3 a1 a2 a3 b0^2 b3 - a1 a2 a3 b0 b1 b2 - 2 a1 a3^2 b0^2 b2 + a1 a3^2 b0 b1^2 + a2^2 a3 b0^2 b2 - a2 a3^2 b0^2 b1 + a3^3 b0^3 + 3 a3 b0^3 x^2 = a0^3 b3^3 - a0^3 y^3 + x (y (-6 a0^2 b0 b3 + 3 a0^2 b1 b2 - a0 a1 b0 b2 - 2 a0 a1 b1^2 + a0 a2 b0 b1 + 2 a1^2 b0 b1 - 3 a1 a2 b0^2) + 3 a0^2 b0 b3^2 + 3 a0^2 b0 y^2 - 3 a0^2 b1 b2 b3 + a0^2 b2^3 + a0 a1 b0 b2 b3 + 2 a0 a1 b1^2 b3 - a0 a1 b1 b2^2 - a0 a2 b0 b1 b3 - 2 a0 a2 b0 b2^2 + a0 a2 b1^2 b2 - 2 a1^2 b0 b1 b3 + a1^2 b0 b2^2 + 3 a1 a2 b0^2 b3 - a1 a2 b0 b1 b2 + a2^2 b0^2 b2) - a0^2 a1 b2 b3^2 - 2 a0^2 a2 b1 b3^2 + a0^2 a2 b2^2 b3 + y (-3 a0^3 b3^2 + 2 a0^2 a1 b2 b3 + 4 a0^2 a2 b1 b3 - a0^2 a2 b2^2 - 2 a0 a1^2 b1 b3 - 6 a0 a1 a2 b0 b3 + a0 a1 a2 b1 b2 + 2 a0 a2^2 b0 b2 - a0 a2^2 b1^2 + 2 a1^3 b0 b3 - a1^2 a2 b0 b2 + a1 a2^2 b0 b1 - a2^3 b0^2) + y^2 (3 a0^3 b3 - a0^2 a1 b2 - 2 a0^2 a2 b1 + a0 a1^2 b1 + 3 a0 a1 a2 b0 - a1^3 b0) + a0 a1^2 b1 b3^2 + x^2 (3 a0 b0^2 b3 - 3 a0 b0^2 y - 3 a0 b0 b1 b2 + a0 b1^3 + 2 a1 b0^2 b2 - a1 b0 b1^2 + a2 b0^2 b1) + 3 a0 a1 a2 b0 b3^2 - a0 a1 a2 b1 b2 b3 - 2 a0 a2^2 b0 b2 b3 + a0 a2^2 b1^2 b3 + a1^3 (-b0) b3^2 + a1^2 a2 b0 b2 b3 - a1 a2^2 b0 b1 b3 + a2^3 b0^2 b3 + b0^3 x^3

求まった式を手作業で整理します。項を左辺に集めて$F_0(x,y)=0$の形に直したりします。
出来上がった式の$x$に$f_0(t)$、$y$に$g_0(t)$を代入して$0$になることをSage Mathで確認しておきます。

確認用

var('a0 a1 a2 a3')
var('b0 b1 b2 b3')
x=a0*t^3+a1*t^2+a2*t+a3
y=b0*t^3+b1*t^2+b2*t+b3
F0=a3^3*b0^3-a2*a3^2*b0^2*b1+a1*a3^2*b0*b1^2-a0*a3^2*b1^3+a2^2*a3*b0^2*b2-2*a1*a3^2*b0^2*b2-a1*a2*a3*b0*b1*b2+3*a0*a3^2*b0*b1*b2+a0*a2*a3*b1^2*b2+a1^2*a3*b0*b2^2-2*a0*a2*a3*b0*b2^2-a0*a1*a3*b1*b2^2+a0^2*a3*b2^3-a2^3*b0^2*b3+3*a1*a2*a3*b0^2*b3-3*a0*a3^2*b0^2*b3+a1*a2^2*b0*b1*b3-2*a1^2*a3*b0*b1*b3-a0*a2*a3*b0*b1*b3-a0*a2^2*b1^2*b3+2*a0*a1*a3*b1^2*b3-a1^2*a2*b0*b2*b3+2*a0*a2^2*b0*b2*b3+a0*a1*a3*b0*b2*b3+a0*a1*a2*b1*b2*b3-3*a0^2*a3*b1*b2*b3-a0^2*a2*b2^2*b3+a1^3*b0*b3^2-3*a0*a1*a2*b0*b3^2+3*a0^2*a3*b0*b3^2-a0*a1^2*b1*b3^2+2*a0^2*a2*b1*b3^2+a0^2*a1*b2*b3^2-a0^3*b3^3+(-3*a3^2*b0^3+2*a2*a3*b0^2*b1-2*a1*a3*b0*b1^2+2*a0*a3*b1^3-a2^2*b0^2*b2+4*a1*a3*b0^2*b2+a1*a2*b0*b1*b2-6*a0*a3*b0*b1*b2-a0*a2*b1^2*b2-a1^2*b0*b2^2+2*a0*a2*b0*b2^2+a0*a1*b1*b2^2-a0^2*b2^3-3*a1*a2*b0^2*b3+6*a0*a3*b0^2*b3+2*a1^2*b0*b1*b3+a0*a2*b0*b1*b3-2*a0*a1*b1^2*b3-a0*a1*b0*b2*b3+3*a0^2*b1*b2*b3-3*a0^2*b0*b3^2)*x+(a2^3*b0^2-3*a1*a2*a3*b0^2+3*a0*a3^2*b0^2-a1*a2^2*b0*b1+2*a1^2*a3*b0*b1+a0*a2*a3*b0*b1+a0*a2^2*b1^2-2*a0*a1*a3*b1^2+a1^2*a2*b0*b2-2*a0*a2^2*b0*b2-a0*a1*a3*b0*b2-a0*a1*a2*b1*b2+3*a0^2*a3*b1*b2+a0^2*a2*b2^2-2*a1^3*b0*b3+6*a0*a1*a2*b0*b3-6*a0^2*a3*b0*b3+2*a0*a1^2*b1*b3-4*a0^2*a2*b1*b3-2*a0^2*a1*b2*b3+3*a0^3*b3^2)*y+(3*a3*b0^3-a2*b0^2*b1+a1*b0*b1^2-a0*b1^3-2*a1*b0^2*b2+3*a0*b0*b1*b2-3*a0*b0^2*b3)*x^2+(3*a1*a2*b0^2-6*a0*a3*b0^2-2*a1^2*b0*b1-a0*a2*b0*b1+2*a0*a1*b1^2+a0*a1*b0*b2-3*a0^2*b1*b2+6*a0^2*b0*b3)*x*y+(a1^3*b0-3*a0*a1*a2*b0+3*a0^2*a3*b0-a0*a1^2*b1+2*a0^2*a2*b1+a0^2*a1*b2-3*a0^3*b3)*y^2-b0^3*x^3+3*a0*b0^2*x^2*y-3*a0^2*b0*x*y^2+a0^3*y^3
F0.simplify_full()

交点を求める

Sage Mathなら9次方程式の解も一発です。

p0x=7; p1x=23; p2x=1; p3x=15
p0y=8; p1y=20; p2y=1; p3y=11
p4x=10; p5x=22; p6x=2; p7x=12
p4y=11; p5y=5; p6y=20; p7y=7
var('t u')
a0=-p0x+3*p1x-3*p2x+p3x
a1=3*p0x-6*p1x+3*p2x
a2=-3*p0x+3*p1x
a3=p0x
b0=-p0y+3*p1y-3*p2y+p3y
b1=3*p0y-6*p1y+3*p2y
b2=-3*p0y+3*p1y
b3=p0y
c0=-p4x+3*p5x-3*p6x+p7x
c1=3*p4x-6*p5x+3*p6x
c2=-3*p4x+3*p5x
c3=p4x
d0=-p4y+3*p5y-3*p6y+p7y
d1=3*p4y-6*p5y+3*p6y
d2=-3*p4y+3*p5y
d3=p4y
x=c0*u^3+c1*u^2+c2*u+c3
y=d0*u^3+d1*u^2+d2*u+d3
F0=a3^3*b0^3-a2*a3^2*b0^2*b1+a1*a3^2*b0*b1^2-a0*a3^2*b1^3+a2^2*a3*b0^2*b2-2*a1*a3^2*b0^2*b2-a1*a2*a3*b0*b1*b2+3*a0*a3^2*b0*b1*b2+a0*a2*a3*b1^2*b2+a1^2*a3*b0*b2^2-2*a0*a2*a3*b0*b2^2-a0*a1*a3*b1*b2^2+a0^2*a3*b2^3-a2^3*b0^2*b3+3*a1*a2*a3*b0^2*b3-3*a0*a3^2*b0^2*b3+a1*a2^2*b0*b1*b3-2*a1^2*a3*b0*b1*b3-a0*a2*a3*b0*b1*b3-a0*a2^2*b1^2*b3+2*a0*a1*a3*b1^2*b3-a1^2*a2*b0*b2*b3+2*a0*a2^2*b0*b2*b3+a0*a1*a3*b0*b2*b3+a0*a1*a2*b1*b2*b3-3*a0^2*a3*b1*b2*b3-a0^2*a2*b2^2*b3+a1^3*b0*b3^2-3*a0*a1*a2*b0*b3^2+3*a0^2*a3*b0*b3^2-a0*a1^2*b1*b3^2+2*a0^2*a2*b1*b3^2+a0^2*a1*b2*b3^2-a0^3*b3^3+(-3*a3^2*b0^3+2*a2*a3*b0^2*b1-2*a1*a3*b0*b1^2+2*a0*a3*b1^3-a2^2*b0^2*b2+4*a1*a3*b0^2*b2+a1*a2*b0*b1*b2-6*a0*a3*b0*b1*b2-a0*a2*b1^2*b2-a1^2*b0*b2^2+2*a0*a2*b0*b2^2+a0*a1*b1*b2^2-a0^2*b2^3-3*a1*a2*b0^2*b3+6*a0*a3*b0^2*b3+2*a1^2*b0*b1*b3+a0*a2*b0*b1*b3-2*a0*a1*b1^2*b3-a0*a1*b0*b2*b3+3*a0^2*b1*b2*b3-3*a0^2*b0*b3^2)*x+(a2^3*b0^2-3*a1*a2*a3*b0^2+3*a0*a3^2*b0^2-a1*a2^2*b0*b1+2*a1^2*a3*b0*b1+a0*a2*a3*b0*b1+a0*a2^2*b1^2-2*a0*a1*a3*b1^2+a1^2*a2*b0*b2-2*a0*a2^2*b0*b2-a0*a1*a3*b0*b2-a0*a1*a2*b1*b2+3*a0^2*a3*b1*b2+a0^2*a2*b2^2-2*a1^3*b0*b3+6*a0*a1*a2*b0*b3-6*a0^2*a3*b0*b3+2*a0*a1^2*b1*b3-4*a0^2*a2*b1*b3-2*a0^2*a1*b2*b3+3*a0^3*b3^2)*y+(3*a3*b0^3-a2*b0^2*b1+a1*b0*b1^2-a0*b1^3-2*a1*b0^2*b2+3*a0*b0*b1*b2-3*a0*b0^2*b3)*x^2+(3*a1*a2*b0^2-6*a0*a3*b0^2-2*a1^2*b0*b1-a0*a2*b0*b1+2*a0*a1*b1^2+a0*a1*b0*b2-3*a0^2*b1*b2+6*a0^2*b0*b3)*x*y+(a1^3*b0-3*a0*a1*a2*b0+3*a0^2*a3*b0-a0*a1^2*b1+2*a0^2*a2*b1+a0^2*a1*b2-3*a0^3*b3)*y^2-b0^3*x^3+3*a0*b0^2*x^2*y-3*a0^2*b0*x*y^2+a0^3*y^3
F0.roots(u,ring=CC)
x=a0*t^3+a1*t^2+a2*t+a3
y=b0*t^3+b1*t^2+b2*t+b3
F1=c3^3*d0^3-c2*c3^2*d0^2*d1+c1*c3^2*d0*d1^2-c0*c3^2*d1^3+c2^2*c3*d0^2*d2-2*c1*c3^2*d0^2*d2-c1*c2*c3*d0*d1*d2+3*c0*c3^2*d0*d1*d2+c0*c2*c3*d1^2*d2+c1^2*c3*d0*d2^2-2*c0*c2*c3*d0*d2^2-c0*c1*c3*d1*d2^2+c0^2*c3*d2^3-c2^3*d0^2*d3+3*c1*c2*c3*d0^2*d3-3*c0*c3^2*d0^2*d3+c1*c2^2*d0*d1*d3-2*c1^2*c3*d0*d1*d3-c0*c2*c3*d0*d1*d3-c0*c2^2*d1^2*d3+2*c0*c1*c3*d1^2*d3-c1^2*c2*d0*d2*d3+2*c0*c2^2*d0*d2*d3+c0*c1*c3*d0*d2*d3+c0*c1*c2*d1*d2*d3-3*c0^2*c3*d1*d2*d3-c0^2*c2*d2^2*d3+c1^3*d0*d3^2-3*c0*c1*c2*d0*d3^2+3*c0^2*c3*d0*d3^2-c0*c1^2*d1*d3^2+2*c0^2*c2*d1*d3^2+c0^2*c1*d2*d3^2-c0^3*d3^3+(-3*c3^2*d0^3+2*c2*c3*d0^2*d1-2*c1*c3*d0*d1^2+2*c0*c3*d1^3-c2^2*d0^2*d2+4*c1*c3*d0^2*d2+c1*c2*d0*d1*d2-6*c0*c3*d0*d1*d2-c0*c2*d1^2*d2-c1^2*d0*d2^2+2*c0*c2*d0*d2^2+c0*c1*d1*d2^2-c0^2*d2^3-3*c1*c2*d0^2*d3+6*c0*c3*d0^2*d3+2*c1^2*d0*d1*d3+c0*c2*d0*d1*d3-2*c0*c1*d1^2*d3-c0*c1*d0*d2*d3+3*c0^2*d1*d2*d3-3*c0^2*d0*d3^2)*x+(c2^3*d0^2-3*c1*c2*c3*d0^2+3*c0*c3^2*d0^2-c1*c2^2*d0*d1+2*c1^2*c3*d0*d1+c0*c2*c3*d0*d1+c0*c2^2*d1^2-2*c0*c1*c3*d1^2+c1^2*c2*d0*d2-2*c0*c2^2*d0*d2-c0*c1*c3*d0*d2-c0*c1*c2*d1*d2+3*c0^2*c3*d1*d2+c0^2*c2*d2^2-2*c1^3*d0*d3+6*c0*c1*c2*d0*d3-6*c0^2*c3*d0*d3+2*c0*c1^2*d1*d3-4*c0^2*c2*d1*d3-2*c0^2*c1*d2*d3+3*c0^3*d3^2)*y+(3*c3*d0^3-c2*d0^2*d1+c1*d0*d1^2-c0*d1^3-2*c1*d0^2*d2+3*c0*d0*d1*d2-3*c0*d0^2*d3)*x^2+(3*c1*c2*d0^2-6*c0*c3*d0^2-2*c1^2*d0*d1-c0*c2*d0*d1+2*c0*c1*d1^2+c0*c1*d0*d2-3*c0^2*d1*d2+6*c0^2*d0*d3)*x*y+(c1^3*d0-3*c0*c1*c2*d0+3*c0^2*c3*d0-c0*c1^2*d1+2*c0^2*c2*d1+c0^2*c1*d2-3*c0^3*d3)*y^2-d0^3*x^3+3*c0*d0^2*x^2*y-3*c0^2*d0*x*y^2+c0^3*y^3
F1.roots(t,ring=CC)

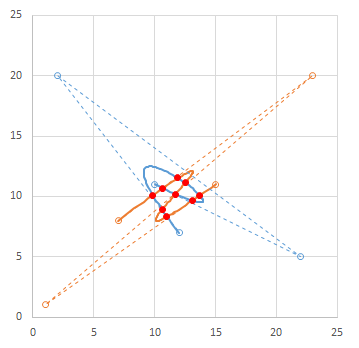
結果

$t$	$x$	$y$
0.0705390793450691	9.84461191120046	10.0977201559658
0.0972454495384701	10.6577721427949	10.6765423110032
0.151317532883142	11.9093731132269	11.5258935928247
0.423317135673883	12.5041615575362	11.1254986683473
0.504784914630604	11.6996978170450	10.1925189113631
0.616234378772213	10.6052155938325	8.90887875422645
0.858627731561791	11.0117797671531	8.32809526476686
0.947328062423360	13.0765930040221	9.65244107470244
0.966598091975171	13.7148564179511	10.0927716028542

$u$	$x$	$y$
0.0192470307676812	10.6577721427949	10.6765423110032
0.0549916382769417	11.6996978170450	10.1925189113631
0.122057002218322	13.0765930040221	9.65244107470243
0.320989106683592	13.7148564179511	10.0927716028542
0.442530534075141	12.5041615575362	11.1254986683473
0.488155778702660	11.9093731132269	11.5258935928247
0.900475882753311	9.84461191120046	10.0977201559658
0.944674407179144	10.6052155938325	8.90887875422645
0.963072466334768	11.0117797671531	8.32809526476686

　

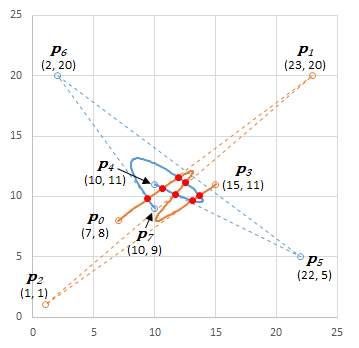
他の例

　

$t$	$x$	$y$
0.0585637754674532	9.43493704741260	9.80138377405827
0.0972456724048092	10.6577783668721	10.6765466824220
0.154353010679454	11.9650417792797	11.5616434144591
0.420784902292453	12.5261497143433	11.1519314423992
0.504773797264918	11.6998148118118	10.1926525928442
0.654000922786538	10.3321138525400	8.54997985319283
0.832480771875075	10.6470861376084	8.13381491403699
0.947409126304024	13.0791259723170	9.65417103848613
0.966443403801796	13.7094396537700	10.0890008674247

$u$	$x$	$y$
0.0192476635566331	10.6577783668721	10.6765466824220
0.0550089406644050	11.6998148118118	10.1926525928442
0.122462462532929	13.0791259723169	9.65417103848613
0.311971168194480	13.7094396537700	10.0890008674247
0.428026614816431	12.5261497143433	11.1519314423992
0.468474338480286	11.9650417792797	11.5616434144591
0.974162274493753	9.43493704741260	9.80138377405827
1.01322055921012	-	-
1.02477551181756	-	-

　

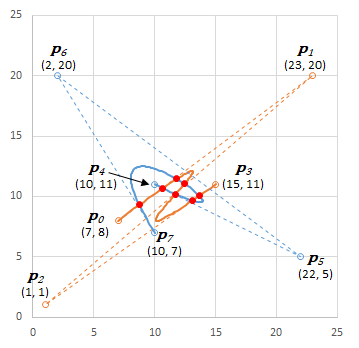
$t$	$x$	$y$
0.0397658991999607	8.73314524643015	9.28828195723746
0.0972452415230028	10.6577663334556	10.6765382308705
0.145557093199524	11.7996461055933	11.4547106185745
0.430283011071176	12.4423716245570	11.0516910994345
0.504793746568507	11.6996048728763	10.1924127107790
0.947291286459872	13.0754442986481	9.65165658411668
0.965461703810384	13.6751752629341	10.0651608525537
0.752680887301335 - 0.0942533376803876*I	-	-
0.752680887301335 + 0.0942533376803876*I	-	-

$u$	$x$	$y$
0.0192472918240925	10.6577663334556	10.6765382308705
0.0550008610109918	11.6996048728763	10.1924127107790
0.122220320258592	13.0754442986481	9.65165658411668
0.317174194109741	13.6751752629341	10.0651608525537
0.434315916130098	12.4423716245570	11.0516910994345
0.479827996329169	11.7996461055933	11.4547106185745
0.931670905582179	8.73314524643016	9.28828195723746
0.983708843870787 - 0.00663807680631019*I	-	-
0.983708843870787 + 0.00663807680631019*I	-	-

　　6次方程式になります。

$t$	$x$	$y$
0.500000000000000　※重根	5.00000000000000	5.00000000000000
0.111397175094424 - 0.755325517520512*I	-	-
0.111397175094424 + 0.755325517520512*I	-	-
1.48860282490558 - 0.563765078306780*I	-	-
1.48860282490558 + 0.563765078306780*I	-	-

$u$	$x$	$y$
0.500000000000000　※重根	5.00000000000000	5.00000000000000
0.111397175094424 - 0.755325517520512*I	-	-
0.111397175094424 + 0.755325517520512*I	-	-
1.48860282490558 - 0.563765078306780*I	-	-
1.48860282490558 + 0.563765078306780*I	-	-

参考文献

1. T.W. Sederberg, T. Nishita
   Curve intersection using Bézier clipping
   Computer-Aided Design, Vol.22, Issue 9, Nov.1990, pp.538-549
   http://nishitalab.org/user/nis/cdrom/cad/CAGD90Curve.pdf

2. ベジェ曲線入門 -- Curve/curve intersection
   https://pomax.github.io/bezierinfo/ja-JP/index.html#curveintersection

3. Thomas W. Sederberg
   Computer Aided Geometric Design, pp.191-208
   Brigham Young University ScholarsArchive -- Faculty Publications
   https://scholarsarchive.byu.edu/facpub/1/

4. T.W Sederberg, D.C Anderson, R.N Goldman
   Implicit representation of parametric curves and surfaces
   Computer Vision, Graphics, and Image Processing, Vol.28, Issue 1, Oct.1984, pp.72-84
   https://www.sciencedirect.com/science/article/abs/pii/0734189X84901403

5. Mathematics Stack Exchange -- Quadratic Bezier curves representation as implicit quadratic equation
   https://math.stackexchange.com/questions/438743/quadratic-bezier-curves-representation-as-implicit-quadratic-equation