これは,湧源クラブ Advent Calendar 20日目 の記事です!
この記事を読むとできるようになること
一見難しそうな拡散方程式を数値計算できる
学部の授業でやった計算を紹介します.
出てくる式は,修論の研究でもめっちゃ使っています.
原始惑星系円盤(Protoplanetary disk)とは
できたてほやほやの恒星の周りにできる,ガスと塵からなる円盤のことです.
質量のほとんど(99%くらい)は水素とヘリウムが主体のガスであると考えられています.
原始惑星系円盤の中で,塵やガスが集まって惑星が誕生します.
現在の太陽系には原始惑星系円盤は残っていませんが,
他の恒星の周りに存在するものは電波望遠鏡で観測されています.
今回は,この原始惑星系円盤のガスの密度進化を解いてみましょう.
拡散方程式
$r$方向(円盤の中心から外側に向かう向き)のガス面密度の拡散方程式は次のようになります.
\frac{\partial\Sigma_{\rm g}}{\partial t}-\frac{1}{r}\frac{\partial}{\partial r}\left[3r^{1/2}\frac{\partial}{\partial r}\left(\Sigma_{\rm g}\nu r^{1/2}\right)\right]=0
$\Sigma_{\rm g}$はガスの面密度と呼ばれる量で,普通の質量密度を$\rho_{\rm g}$として次で定義されます(次元は${\rm ML^{-2}}$).
\Sigma_{\rm g} = \int_{-\infty}^{\infty} \rho_{\rm g} dz
$\nu$は粘性係数です(次元は${\rm L^2T^{-1}}$).
拡散方程式の導出は記事の後ろに書いてあるかもしれないです.
無次元化
では,この式を計算していきたいのですが,明らかに複雑でめんどくさそうですよね.
数値計算を行うときによく用いられる手法として,無次元化というものがあります.
様々な物理量(今回の場合,$r, \Sigma_{\rm g}, \nu, t$)をそれぞれ適当な値で規格化することで,式をスッキリさせて計算しやすくします.
円盤の典型的な半径,円盤の典型的な寿命,中心($r=0$)での面密度をそれぞれ
$r_1, t_0, \Sigma_0$とします.
そして,次のように無次元の数$x, \sigma, \tau$を用いてそれぞれの物理量を変数変換します.
r \equiv x^2 r_1\\
\Sigma \equiv \sigma \Sigma_0\\
t \equiv \tau t_0
$\nu$についてはとりあえず置いておきましょう.
これらを元の方程式に代入すると,
\frac{\partial \sigma}{\partial \tau} - \frac{3t_0}{4r_1^2} \frac{1}{x^3} \frac{\partial^2}{\partial x^2}(\sigma \nu x) = 0.
ここで,$\nu \propto r$ と仮定し,
$\nu = 4r_1^2/(3t_0) x^2$ とおきます.
すると,次のようになります.
\frac{\partial \sigma}{\partial \tau} - \frac{1}{x^3} \frac{\partial^2}{\partial x^2}(\sigma x^3) = 0
$y = \sigma x^3$とおくと,
\frac{\partial y}{\partial \tau} - \frac{\partial^2 y}{\partial x^2} = 0
となって,よく見る拡散方程式の形になります.
これを計算して,最後に変数変換したものを元に戻せばOKです.
計算結果
Fortranで書いた計算コードを記します(学部時代に書いたのそのまま).
サンプルコード
program main
implicit none
! r方向の刻み
INTEGER, parameter :: jmax = 200
! 時間ステップ数
INTEGER, parameter :: nmax = 10000000
! 出力時間ステップ
INTEGER, parameter :: nint = 10000
REAL, dimension(0:jmax) :: u
REAL, dimension(1:jmax-1) :: unew
REAL delx, delt, r, x
INTEGER j,n
INTEGER i
CHARACTER(len = 20) fname
i = 0
delx = 1.0 / real(jmax)
delt = (delx**2) /3
! クーラン数
r = delt / delx*2
!初期条件
u(0) = 0.0
DO j = 1, jmax-1
x = real(j)*delx
u(j) = x*exp(-(x/0.1)**2)
END DO
u(jmax) = 0.0
DO n = 0, nmax
IF (mod(n, nint) == 0) THEN
write(fname,'(i5.5,a)') , i, '.dat'
open(10, file = fname)
DO j = 1, jmax
x = real(j)*delx
! 元々の変数に変換して出力
write(10,'(2f12.5)') x**2, u(j)/(x**3)
END DO
CLOSE(10)
i = i +1
END IF
! 拡散方程式の差分方程式
DO j = 1, jmax-1
unew(j) = u(j+1)*r + u(j)*(1.0 - r*2.0) + u(j-1)*r
END DO
! 値の更新
DO j = 1, jmax-1
u(j) = unew(j)
END DO
END DO
END program main
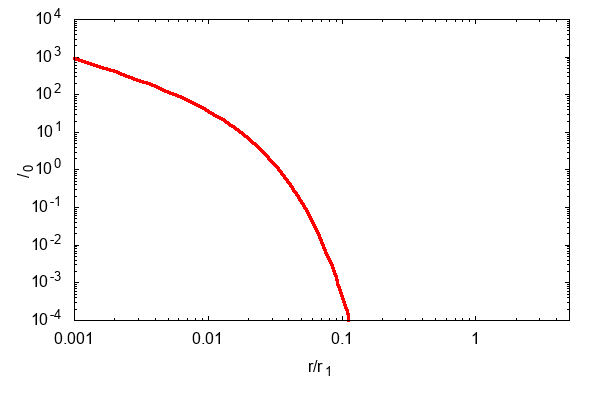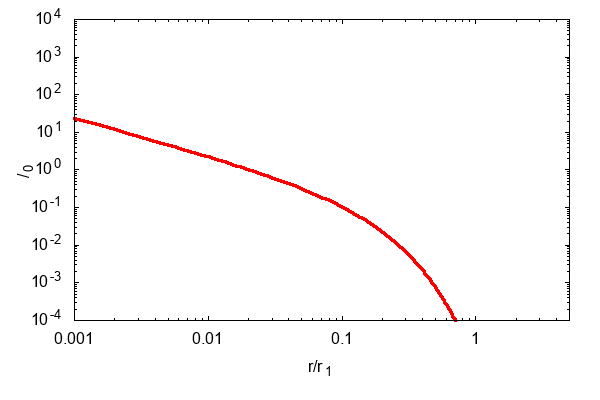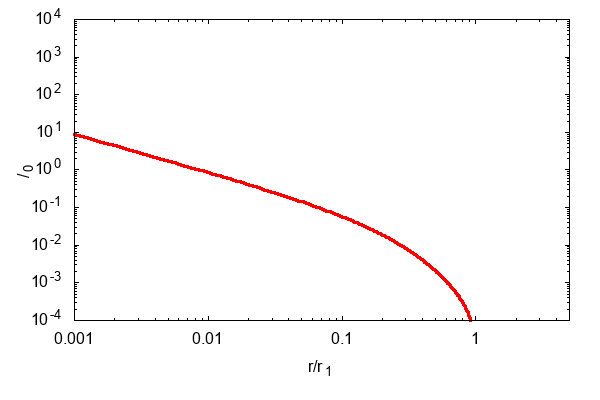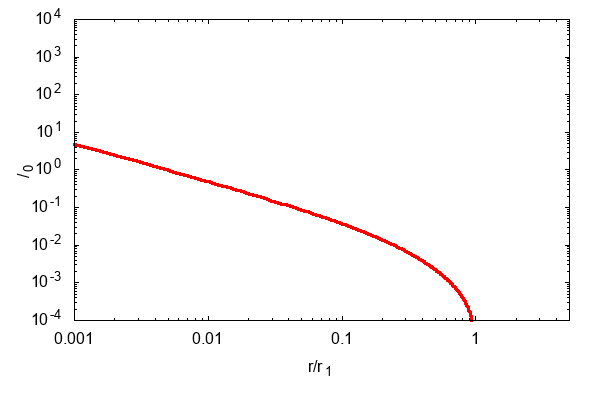
計算すると,こんな感じで面密度が拡散していきます
(横軸縦軸ともに,適当な値で規格化しています).
(昔書いたコードを使ったので,動画はgnuplotで作りました)
自己相似解
さて,上の動画をキャプチャするとこんな感じになります.
色が濃くなるにつれて時間が進んでいくことを表しています.
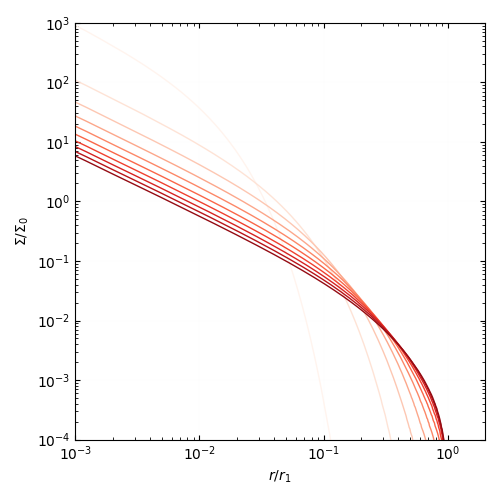
よく見ると,各時刻の面密度のグラフは
他の時刻の面密度のグラフを伸び縮みさせた形になっています.
このような解を自己相似解といいます.
付録:拡散方程式の導出
力尽きたので,読者への宿題とする.
付録:拡散方程式の解析解
ここまで頑張って書いておいてなんですが,
実はこの方程式,特別な場合には解析解が存在します.
\nu = \nu_1(r/r_1)^{\gamma}\qquad (\nu_1 は r=r_1 での \nu)
と仮定すると,
\Sigma_{\rm g} = \frac{C}{3\pi \nu_1 (r/r_1)^{\gamma}} T^{-\frac{5/2-\gamma}{2-\gamma}} \exp\left[ -\frac{(r/r_1)^{2-\gamma}}{T} \right].
ここで,$C$は積分定数,
T = \frac{t}{t_{\rm dif}} +1,\\
t_{\rm dif} = \frac{1}{3(2-\gamma)^2}\frac{r_1^2}{\nu_1}
半径Rより内側の円盤の質量は,
M_{\rm d}(R, t) = \int_0^R 2\pi r \Sigma_{\rm g} {\rm d}r
と書けます.円盤全体の質量は,$R\rightarrow \infty$として求まり,
$\Sigma_{\rm g}$の式を使って頑張って計算すると,
$C$が求まります.
\Sigma_{\rm g} = \frac{M_{\rm d}(0)}{2\pi r_1^2 (r/r_1)^{\gamma}} T^{-\frac{5/2-\gamma}{2-\gamma}} \exp\left[ -\frac{(r/r_1)^{2-\gamma}}{T} \right]
