Serializablitiyとは？ 2. View Serializabilityについて

前回のまとめ

FSRという基準を導入したが実用性がイマイチなので別の基準を考える。

View Equivalency

さて、最後の状態が一致するかどうかでスケジュールの等価性をテストすると不都合が起きてしまうので、それにさらに制約を加えて行く。2つのスケジュール図の最後の状態の一致のみを見てはダメなので、2つのスケジュール図のトランザクションのすべてのステップでのエルブランセマンティクスが一致した場合に満たされるのがView Equivalency（ビュー等価）である。
もちろん最後の状態も「すべてのステップ」のうちの1つなのでView Equivalencyを満たす場合Final State Equivalencyも確実に満たす。また、トランザクションを直列に逐次実行したスケジュールとView Equivalencyが満たされる場合、そのトランザクションは View Serializable(以下VSR)と呼ばれる。
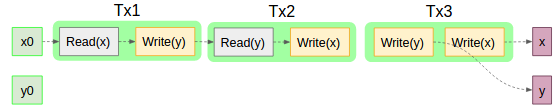
これで例えばさっきの物がどうなるかというと、トランザクションaのi番目のステップをTxa_iと表記するとして

↑のエルブランセマンティクス

Tx1_1 = x0
Tx1_2 = F1(x0)
Tx2_1 = y0
Tx2_2 = F2(y0)
Tx3_1 = F3()
Tx3_2 = F3()
x = F3()
y = F3()

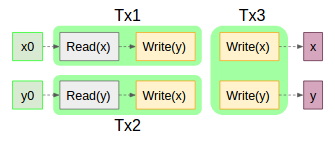
とそれぞれ表される。先ほどFinal State Equivalentだった以下のスケジュールについて

↑のエルブランセマンティクス

Tx1_1 = x0
Tx1_2 = F1(x0)
Tx2_1 = Write(y) = F1(Read(x)) = F1(x0)
Tx2_2 = Write(x) = F2(Read(y)) = F2(Write(y)) = F2(F1(Read(x))) = F2(F1(x0)))
Tx3_1 = F3()
Tx3_2 = F3()
x = F3()
y = F3()

となり、Tx2_*のエルブランセマンティクスが一致しないのでVSRではない。x,yは一致しているのでFSRではある。

↑のエルブランセマンティクス

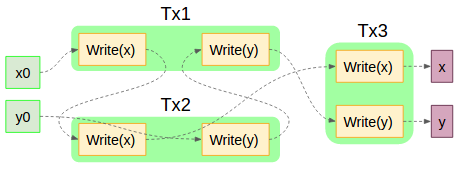
Tx1_1: F1()
Tx1_2: F1()
Tx2_1: F2()
Tx2_2: F2()
Tx3_1: F3()
Tx3_2: F3()

このスケジュール図はVSRを満たす(Tx1→Tx2→Tx3もしくはTx2→Tx1→Tx3の逐次実行とビュー等価)。だがもしTx3が居なかった場合に残される結果は「xはTx2が書いたもの」「yはTx1が書いたもの」という歪な形になる。この特性はアボートなどが今後含まれる事を考えると好ましくないので、ビュー等価でも人類はまだ満足できていないということになる。

なお、スケジュールがVSRの条件を満たすか否かはNP完全問題であることが証明されている。P=NPが証明された暁には特定の前提が満たされた状態でのトランザクションスケジューリングに大きなブレークスルーが起きるかも知れない。

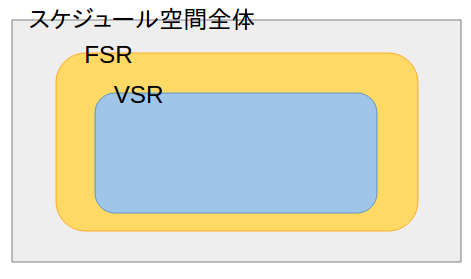
ここまでで、スケジュール空間の中におけるFSR, VSRの包含関係は

このようになっている。