Serializableとは何か
複数のトランザクションの実行スケジュールが渡された時、その挙動について論じる際の基準の1つがSerializabilityである。と、単純に一言で片付けば良いのだけれど実際にはこの中にも複数の階層と紆余曲折がある。それらについて追っていく。
Final State Equivalency
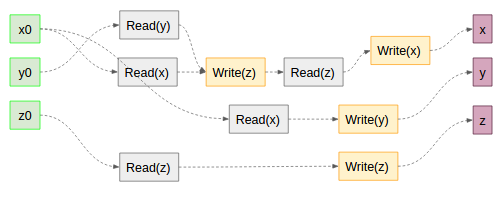
さて、Writeする値はそのトランザクションがそれまでにReadしてきた値から算出された値なので、Write操作は「そこまでのReadを引数に取る多引数関数」と見なす事ができる。説明上、トランザクションの数字と関数に付ける識別子を揃えて表記する。例えばTx1が実行する操作を多引数関数で表す時はF1を用いる。そしてReadは「その前に行われたWriteの結果そのもの」と見なせるので、例えばxの最終状態についてこのように書き下す事ができる。
x = Write(x) # xの最終状態はxにWriteした結果だから
= F4(Read(z)) # zの値を読んで何らかの関数F4を行った結果だから
= F4(Write(z)) # Read(z)される値はその前にWrite(z)した結果だから
= F4(F1(Read(x), Read(y))) # zはxとyの値を読んで何らかの操作F1を行った結果だから
= F4(F1(x0, y0)) # xの最終状態はxとyの初期状態に関数F1とF4を適用した結果である
y = F2(x0) # 途中式省略
z = F3(z0) # 途中式省略
こうやって全部の値に対して操作を書き下していくと最終状態を初期状態と関数の式で表現する事ができる、この式の事を専門用語で**「エルブランセマンティクス」と呼ぶ。2つのスケジュール図が与えられた時に全部の値に対してエルブランセマンティクスが一致すれば、2つのスケジュール図は全く同じ結果に至る事がわかる。これをFinal State Equivalent**と呼ぶ。
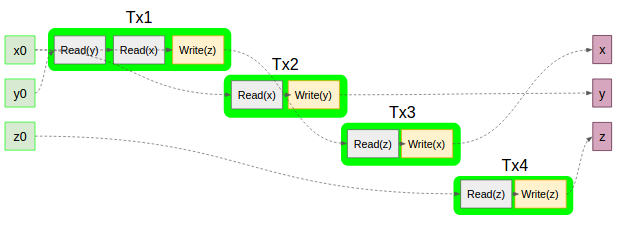
一見して別物に見える以下のスケジュール図も
エルブランセマンティクスを整理すれば
x = F4(F1(x0, y0))
y = F2(x0)
z = F3(z0)
となる。これは上の図と全く同一なので、この二つのスケジュールはFinal State Equivalentである。
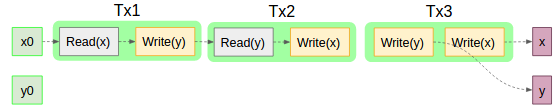
もちろんトランザクションを何らかの順で1つずつ直列(Serial)に実行した場合にもエルブランセマンティクスは定義できる。
このスケジュール図の通りに実行した結果から得られるエルブランセマンティクスは、先ほどのエルブランセマンティクスと(たまたま)完全に一致しているのでFinal State Equivalentである。このように「1つずつ直列に実行した」スケジュールとFinal State Equivalentな場合に対して特別にFinal State Serializability(以下FSR)と呼ぶ。
Serializableというのは「直列に実行した場合と同じ結果となる」と言い換えても良い。
さて苦労して定義したFSRだが実用的ではない。何故なら最終状態のエルブランセマンティクスしか相手にしていないので、例えば以下のトランザクション群の場合に困った事になる。
Tx1: Read(x) Write(y)
Tx2: Read(y) Write(x)
Tx3: Write(x) Write(y)
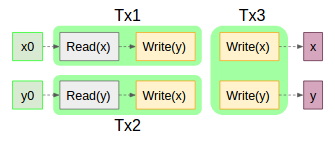
極端な例だが以下のようなスケジュール図が作られたとする。
x = F3()
y = F3()
である。Tx3が何も読まずに値を書いたので何らかの定数を書き込んだ事になっており、そこより前のトランザクションの結果は有っても無くてもグチャグチャでも構わない事になってしまう。実際にはTx1とTx2の間でWrite Skew Anomaly(詳細は後日)という矛盾が起きているにも関わらず、以下のSerial実行とEquivalentである。「終わりよければ全てよし」というか「終わりだけ一致していれば途中経過がどうなってもおかまいなし」に近い。
x = F3()
y = F3()
他にも、Read Onlyなトランザクションが居た場合、そのトランザクションが一貫性の無い値を読んだとしてもFSRは成立してしまう。
さらには、2つのスケジュール図がFinal State Equivalentであることを示すためにはそれぞれのスケジュールに登場した値のエルブランセマンティクスを追い、一致しているかを確かめれば良いので多項式時間で完了させることができる一方でFSRを満たしているかどうかをチェックするためには、トランザクション数Nに対してN!パターンある逐次実行パターンとそれぞれ一致するかを比較する他無く、実用的な速度が出ない。そもそもこれ単品では研究上では実用とされているモノを見たことがないが、議論の出発点として理解しやすいのでよく引き合いに出される。