Paxosとは何か
分散システムの金字塔とも呼ばれ、Leslie Lamport大先生の輝かしい成果の一つとして知られる分散合意アルゴリズムPaxos。
既存の解説
実はすでに存在するPaxosの解説は充分に質が高い
- Wikipediaの項目にも結構長々と書かれていて、これを読んで理解できた人はもう僕の記事を読む必要はない。
- 同様にPFIの久保田さんによる解説スライドもあり、これも良く書けているし、これを読んで理解できた人もこれ以上記事を読む必要はない。
- minghai氏によるブログ記事のこれとか特にこっちなんかはかなり納得感があり、これらを読んで理解できた人も(中略)
- tyonekura氏によるスライドも良くかけていて(中略)
この記事はこれらの説明に目を通してもなお理解できなかった人、もしくはこれらの説明をこれから読もうと思っている人に向けて書き、Paxosアルゴリズムの詳細な説明自体はそれらの記事に譲る。
何故Paxosは理解されないか
Paxosの説明を読んだのにわからなくてさー、と僕のところに聞きに来る人はおおよそ以下のパターンのどれかに分類される。
最初の論文が難解
いきなり原典であるThe Part-Time Parliamentを読みに行く人は大抵挫折する。現状これだけ日本語で解説されているものがあるので理解が目的であれば原典の方は暇なときに読む読み物として考えるぐらいで充分である。
ビザンチン将軍問題はこのLeslie Lamport大先生が提唱した分散システムの輝かしい研究成果の一つであり、このノリで「Paxos議会問題」とでも呼ぶべき難問として定義する心意気で研究をしてきた果てに出てきたのがこの成果と思われる。抜粋すると
I decided that what they were trying to do was impossible, and set out to prove it. Instead, I discovered the Paxos algorithm, described in this paper.
私は当初、合意するのは不可能であると判断してそれを証明するために出発したのだが、
代わりにこの論文で示されているPaxosアルゴリズムを発見するに至った。(拙訳)
そんな裏話は面白いといえば面白いのだが、いきなり読みに行ってもPaxosアルゴリズムそのものを理解する助けにはならない。後回しにしよう。
必要以上に難しいと喧伝されている
そんな過去の論文があるせいか難しいと必要以上に喧伝されている事がある。
興味深い例としてはPaxos Made Liveのpaperが難しい、更にはこのpaperの中でもPaxosがツラいと書いてある事をもってしてPaxosアルゴリズムの事を難しいとする根拠にしている場合も見たことがある。
Paxos Made Liveは「ChubbyというGoogle社内での高信頼な分散ロックサービスを実現するためにPaxosを利用したら結構大変だった」という内容を説明している論文ではあるがPaxosアルゴリズムそのものの事を難しいとは書いていない(多分)。Paxosが前提としている「メッセージが際限なく遅延・順序逆転などが起きうる環境下」で同様の特性を保ちながら分散ロックサービスを実現することが難しいと書いている。Paxosと分散ロックサービスの間の違いには大きな隔たりがあり、その違いを適切に汲み取るのはやはり専門家であっても難しい問題ではある。が、Paxosアルゴリズムそのものを学ぶ場合においてはこの議論は無視しても構わない。
何を達成したのか誤解してかかる人が多い
Paxosアルゴリズムとは「ただ一つの覆らない値を選択する」アルゴリズムであり、誤解を恐れずに言うとこれ単品ではロクな使い道がない。
しかしその「値を選択する」という説明を聞いて「分散キーバリューストアがいい感じに作れるんだね!」などと勝手に拡大解釈してドツボにハマる人は良く見てきた。かく言う僕もそのうちの一人である。分散キーバリューストアであれば、複数のキーバリューペアが次々と追加・更新・参照・削除できる事を当然期待し、そのためにはデータストアの状態を次々と書き換えていく事が前提となる。しかしPaxosアルゴリズム単品ではどうやってもその期待に応えることはできない。なのでPaxosアルゴリズムの説明を隅々まで眺めながら「なるほど、わかった気がするけどこれでキーバリューストアは実装できないのでは?」と勝手に失望する事になる。
Paxosで一度合意(選択)した値はアルゴリズム上二度と覆らない。一度確定したら二度と変化しない値というのはプログラミングの部品としてはimmutableなどという名前と共によく出てくるが、単品では立派なソフトウェアにはならない、例えば分散キーバリューストアを実現するのであればChubbyのように更にPaxosを拡張したMulti-Paxosなどに頼ることになる。
つまりPaxosは何をどうするのか。
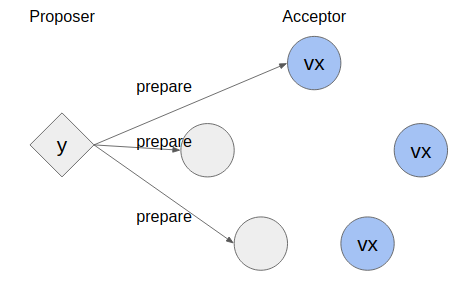
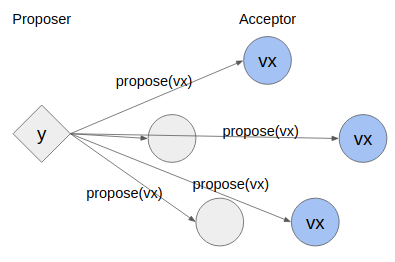
複数のProposer(1,2,...k)が思い思いの値(v1,v2,...vk)と提案番号(n1,n2,...nk)を持ち寄り、Acceptorのクラスタの中でv1,v2,...vkのどれかの値を選択することに合意することを目標にしている。選択された値は二度と覆ることはない。
擬似コード
以下に、現時点での理解における擬似コードを書く。
細部は論文とは異なるかも知れないし、もう少し効率的な実装方法もあるかとは思うが、論文の趣旨には反していないと考えている。
class Proposer:
def propose(self, v):
n = random() # 何らかの正の数が出るとする
while True:
# すべてのacceptorに対してprepareを試みる
responses = []
for acceptor in acceptors:
responses.append(acceptor.prepare(n))
# 戻り値に一つでもngが含まれていたら提案を初めからやり直す
restart_flag = False
for resp in responses:
if resp == None: # 返答が返ってきてなければ無視
continue
msg, num, v = resp
if msg == "ng":
n = num + 1 # nを大きくして次の提案は成功するようにする
restart_flag = True
break
if restart_flag:
continue # ngが返ってきていたのでやり直し
# もしくは返答が過半数を超えなかったら最初からやり直し
count = 0
for r in responses:
if r != None:
count += 1
if count < len(responses):
continue # 過半数未満
# 自分が採用するvを決める
max_num = 0
for resp in responses:
if resp == None: # 返答が返ってきてなければ無視
continue
msg, num, proposed_v = resp
if max_num < num and proposed_v != None:
max_num = num # 最大の提案番号numで
v = proposed_v # 自分の提案すべきvを変更する
# もしresponsesのproposed_vがすべてNoneだったらここでのvは初めから持ってきたvのまま
# 提案(propose)をする
success = True
for acceptor in acceptors:
if success:
success = acceptor.propose(n, v)
if success:
break # 全員からTrueが返ってきた場合だけpropose終了
class Acceptor:
def prepare(self, n):
if self.my_num < n: # 自分が過去に約束した提案番号より大きいならOKを返す
self.my_num = n
return ["ok", n, self.proposed_v]
else: # 小さいなら既に受領した提案番号を返す
return ["ng", self.my_num, None]
def propose(self, n, v):
if self.my_num <= n:
self.proposed_v = v
self.my_num = n
return True
else:
return False
「選択される」の定義
Paxosに於いて選択されるとは「Acceptorの過半数が同じvxを選んだ」という状態になること。(xというのはv1...vkのどれか一つという意味)
ひとたび選択されたら覆らないのだから、その状態で*prepare(np)をしにくるProposer p は選択済み状態を観測したら提案番号が低いために諦めるか、すでに選択済みのvxを上書きするようなpropose(np,vx)*を投げなくてはならない。
Proposerはprepareに対し過半数からokを貰った時点でしか*propose()*に進むことはできないので、*propose()*リクエストは必ず選択済みの値vを踏まえたもの(=提案する値はvxそのもの)になる。
Paxosをコーナーケースでいじめてみる
さて、Paxosにとって可能な限り複雑そうな状況に追い込んでみて値が反転するような事態に陥るかを検討してみよう。
PaxosプロトコルをProposeまで進める最小ステップは過半数からのprepareへの合意である。
ここで、提案番号2を持つProposerが値vを引っさげてproposeまで進んだとする。
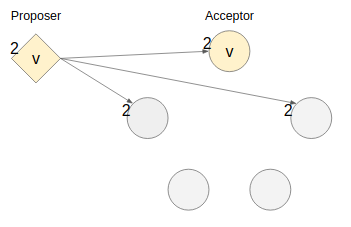
prepare及びproposeリクエストそのものは全acceptorに飛ばしているが、このままだと成功してしまうので一番ややこしそうな最小ケースとしてギリギリ過半数にだけprepareが届き、1件だけproposeが届いて他のパケットはドロップしてしまった状態を作ると上の図になる。
現状ではまだAcceptorの過半数は同じ提案された値を持っていないので値は選択されていない。
ここで新たなProposerがやってきて別の値uを提案しようともう少し大きい提案番号3を持ってきたとする(提案番号を小さくしてもいいのだがそれはそのままacceptorから却下されるので何も自体を複雑にしてくれない)。
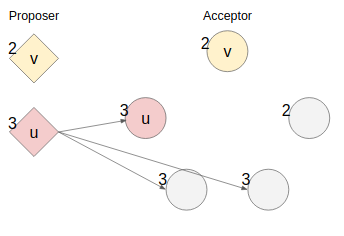
ここで、prepareを全acceptorに飛ばしているのだが、既にvをacceptしているacceptorには運悪く届かなかったとして、最小限のprepareの成功を経て、残る別のAcceptorの一つだけにproposeが成功するとする。現状でもまだAcceptorの過半数は同じ提案された値を持っていないので値は選択されていない。
同様にしてまた新たなProposerが現れて提案番号4かつ新たな値wに決定させようとprepare/proposeを行う。
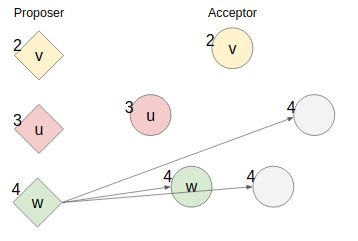
例によってprepareは都合よく既にpropose済みのacceptorには届かず、最小限のprepare成功をもってしてproposeへ進み、1件だけproposeに成功する。
現状でもまだAcceptorの過半数は同じ提案された値を持っていないので値は選択されていない。
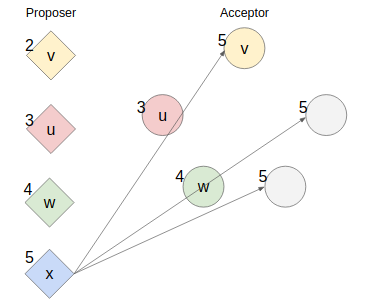
更に新たなProposerが現れて提案番号5かつ新たな値xに決定させようとprepare/proposeを行う。
しかしここでついに過半数を得るために既存のaccept済みのacceptorにprepareを送らざるを得なくなりaccept済みの値vを含むokレスポンスを取得してしまう。するとProposerは同じ提案番号5に対して既存のvをxの代わりに採用するためvを全体に展開する他無くなってしまう。
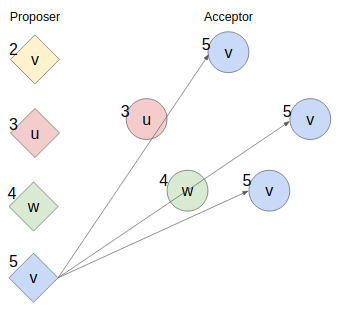
これが仮にいい具合に提案番号3のProposerXが割り込んできても
- 提案番号5のProposerのprepareより前に先にXのprepareが全Acceptorに到達: 提案番号5でprepareが上書きされるだけ
- 提案番号5のProposerのprepareより前に先にXのproposeが過半数のAcceptorに到達: 提案番号5のProposerがそのacceptされた値を観測して採用してそのまま続行
- 提案番号5のProposerのproposeより前に先にXのprepareが全Acceptorに到達: 提案番号5でprepare済みなのでそれより小さいprepareは拒否される
- 提案番号5のProposerのproposeより前に先にXのproposeが過半数のAcceptorに到達: 提案番号5でprepare済みなのでそれより小さいproposeは拒否される
という感じに、一度過半数を超えたものが裏返ることはない。
一度過半数を超えてしまった値を覆させるには、過半数のprepare成功を得る事なく充分大きな提案番号でproposeを投げつける他なく、それはPaxosプロトコルに違反する。
意図的にプロトコルに違反してくるProposerはPaxosアルゴリズムの範疇外となる(耐える亜種はあるらしいがPaxosそのものではない)のでPaxosアルゴリズムの穴ではない。
Multi-Paxosについて少し
Multi-Paxosは同じProposerが提案番号なりを引き継いで連続して提案をし続けるプロトコルだと勘違いされているが実はそれは誤解を含んでいるケースがある。
Multi-Paxosは何度もPaxosを実行することで「覆らない値」の「系列」を順番に合意していくものではあるが、個々のPaxosは独立して実行されており、その際には提案番号nとは全く別に増加する合意系列上の添字番号iを持つ。そしてそれぞれの添字番号に対して独立したPaxosをそれぞれ実行する。実装レベルでいうと**prepare()**などに引数iが増える形になる(もちろんそれ以外の実装法もあるが)。全部の個別のPaxosでProposerが別個に動くと面倒さが増えるのでそれを数秒の単位で連続して同じプロセスが単一のProposerであり続ければ故障頻度と通信遅延の間で速度のバランスが取れるね、というのがMulti-Paxosにおける最適化である。
まとめ
Paxos恐るるに足らず。だが単品では実用性はないため適宜Multi-PaxosやRaftなどを使っていこうな。