なでしこを使って、パズルのハノイの塔を解いてみましょう。
ハノイの塔とは
ルールに沿って杭に刺した円盤を移動させるパズルです。
ハノイの塔(ハノイのとう、Tower of Hanoi)は、パズルの一種。 ... ハノイの塔は、フランスの数学者エドゥアール・リュカが1883年に発売したゲーム『ハノイの塔』がルーツである ...
解が再帰的な構造をしているということから、この解の手順を表示させるという問題は、再帰的なコンピュータ・プログラムの単純な例題として多用されている。
ハノイの塔(Wikipedia)
ハノイの塔のルール
以下のルールに従ってすべての円盤を右端の杭に移動させられれば完成です。
- 3本の杭と、中央に穴の開いた大きさの異なる複数の円盤から構成される。
- 最初はすべての円盤が左端の杭に小さいものが上になるように順に積み重ねられている。
- 円盤を一回に一枚ずつどれかの杭に移動させることができるが、小さな円盤の上に大きな円盤を乗せることはできない。
解法は?
解法もWikipediaにありますので、詳しくはそちらを確認しましょう。
再帰を使うと簡単に解くことができます。
なでしこ3で解く方法
なでしこ3で解くには、次のようなプログラムを記述します。簡易エディタか、貯蔵庫で次のプログラムを実行してみましょう。
●(SRCからDESへ)円盤移動とは
「・{SRC}から{DES}へ移動」と表示。
ここまで。
●(円盤数をSRCからDESへTMPで)ハノイ解読とは
もし、円盤数=1ならば:
SRCからDESへ円盤移動
もし、円盤数が2以上ならば:
# 円盤数より上の円盤を待避用の杭に移動
(円盤数-1)をSRCからTMPへDESでハノイ解読。
# 一番下の円盤を目的地に移動
SRCからDESへ円盤移動
# 待避用の杭に移動した円盤を目的地に移動
(円盤数-1)をTMPからDESへSRCでハノイ解読。
ここまで。
# 解法を表示する
3を「A」から「C」へ「B」でハノイ解読。
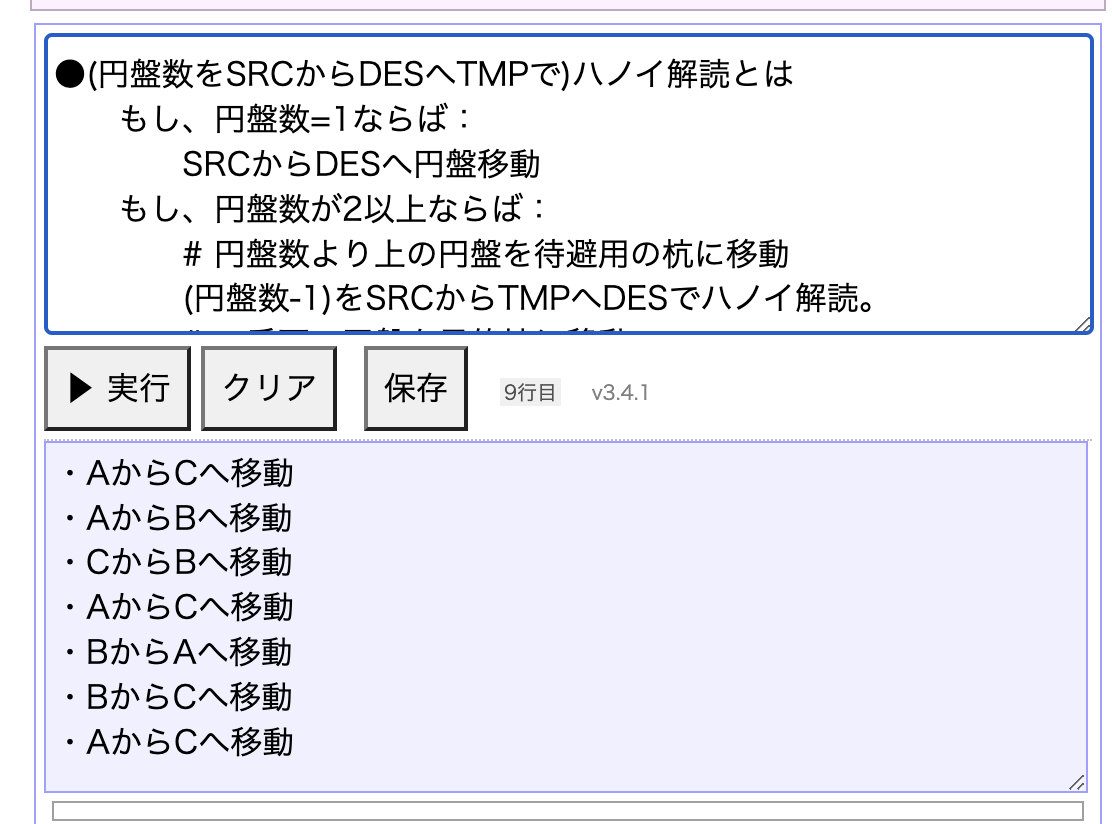
実行すると下記のようになります。
まとめ
再帰を使うと、簡単にハノイの塔を解けます。再帰って便利ですね。