人はなぜ「アナログ時計」を作りたくなるのでしょうか?
それは、そこに円や線を描画できるプログラミング言語があるからです!
タートルグラフィックスでアナログ時計を描画する
既に、アナログ時計の作り方は、いろいろなところで紹介しています。
例えば、以下はタートルグラフィックスの機能を使った、アナログ時計の作り方を紹介しています。
そこで、今回は、上記を改良しつつ、タートルグラフィックスを使わないで作ってみましょう。
SIN/COSで時計の盤を描く
アナログ時計作りに欠かせないのが、SIN関数とCOS関数です。
SINとCOSは三角関数です。でも、時計を描画するだけなら、あまり難しいことを考える必要はありません。これを使うと、針の角度に応じた座標を調べることができることが分かればOKです。
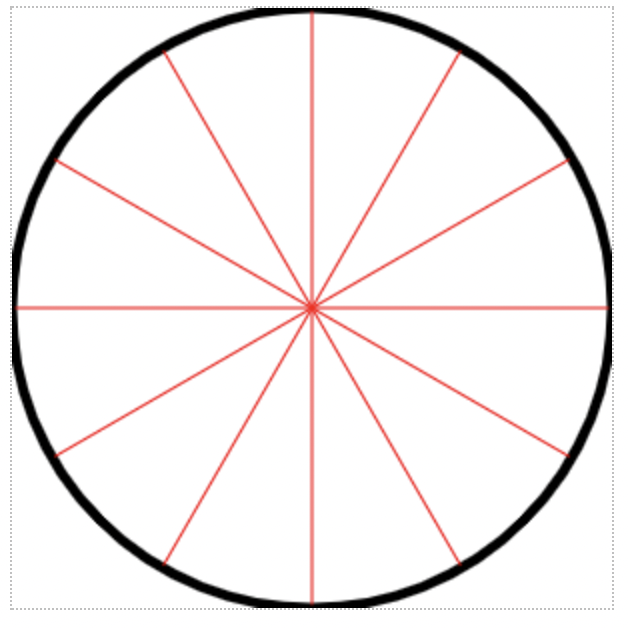
まずは、以下のようなアナログ時計の盤を描画してみましょう。
上記の盤を描画するのが、以下のプログラムです。
# 時計のサイズを指定
CW=300 # サイズ
CX=CW÷2 # 中心点
CY=CW÷2
盤描画。
●盤描画とは
# 盤背景
全描画クリア。
5に線太設定。
白色に塗色設定。
黒色に線色設定。
[CX,CY]へCXの円描画。
# グリッド線
長さ=CX×0.99
12回
角度=(回数-1)/12×360
赤色の1を長さと角度で針描画
ここまで。
ここまで。
●(色のサイズを長さと角度で)針描画
角度=(角度-90)%360;
色に線色設定。
サイズに線太設定。
X=長さ×COS(角度÷180*PI)
Y=長さ×SIN(角度÷180*PI)
[CX,CY]から[X+CX,Y+CY]へ線描画。
ここまで。
時計を完成させる
あとは、1秒おきに針の角度を指定して針描画を呼べば時計の完成です!
# 時計のサイズを指定
CW=400 # サイズ
CX=CW÷2 # 中心点
CY=CW÷2
時計更新。
「時計更新」を1秒毎。
●盤描画とは
# 盤背景
全描画クリア。
1に線太設定。
白色に塗色設定。
黒色に線色設定。
[CX,CY]へCXの円描画。
# グリッド線
長さ=CX×0.99
12回
角度=(回数-1)/12×360
灰色の1を長さと角度で針描画
ここまで。
ここまで。
●(色のサイズを長さと角度で)針描画とは
角度=(角度-90)%360;
色に線色設定。
サイズに線太設定。
X=長さ×COS(角度÷180*PI)
Y=長さ×SIN(角度÷180*PI)
[CX,CY]から[X+CX,Y+CY]へ線描画。
ここまで。
●時計更新とは
盤描画。
# 現在時刻を得る
今を「:」で区切る。
変数[時,分,秒]=それ
# 角度計算
時角度=(時%12)÷12×360+((分/60)×(360÷12))
分角度=分÷60×360
秒角度=秒÷60×360
# 針を描画
黒色の12を(CX×0.5)と時角度で針描画。# 時
青色の8を(CX×0.8)と分角度で針描画。# 分
赤色の4を(CX×0.95)と秒角度で針描画。# 秒
ここまで。
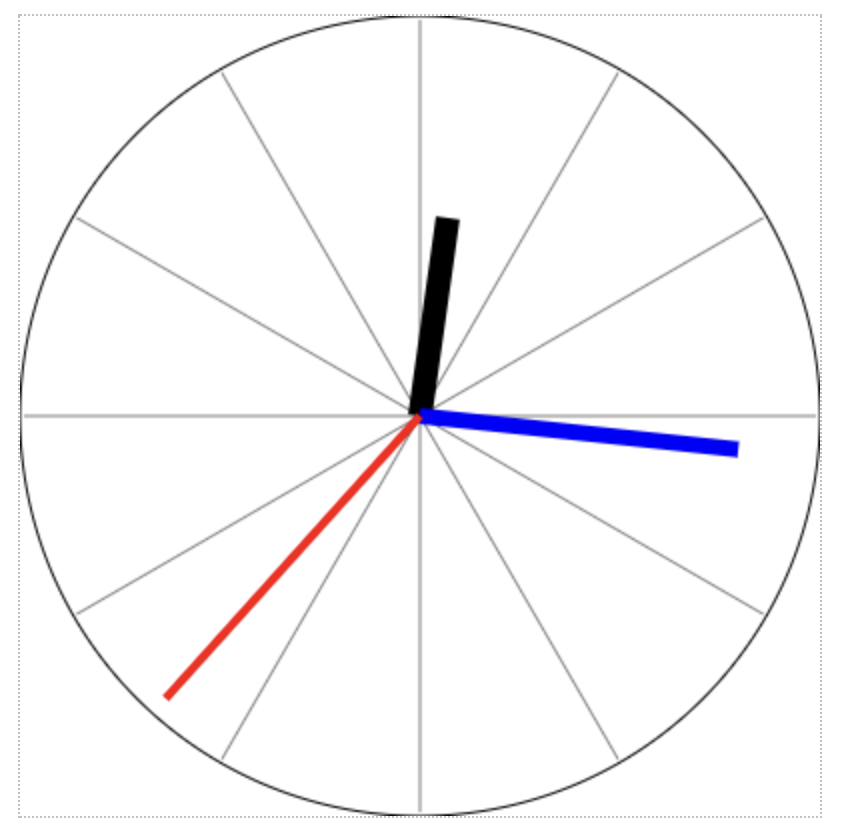
上記をなでしこ貯蔵庫で実行すると、次のような時計が表示されます。
楽しいですね!
針の描画方法をもう少し工夫すれば豪華な時計になります。
ぜひ、挑戦してみてください!