変分問題は 汎関数 (関数を変数とする関数)を対象に、その最小化や最大化などを扱います。
関数を変数とする関数、ということで JavaScript で関数プログラミングするとどんな感じになるんだろうと思って試してみました。
- なお小生、いまだに JavaScript に不自由な方、です。。。(自慢すんな!)
- 一部だけですが、恐る恐る ECMAScript 6 の機能を使ってみました
例題
ここでは古典力学のラグランジアンと最小作用の原理を例にします。また簡単のため1粒子の1次元運動のみを扱います。
-
ラグランジアンとか分からなくっても、要は (1') みたいな関数に、
- 境界条件 (4) を満たす任意の関数 x(t) を代入して (2) の積分を計算し、
- この積分値が最小となるような x(t) を求めると、
- それが実際に起こる運動になる、というものです。
-
正しくは、(3) 式は 最小ではなく停留 条件なのですが、一般に最小作用の原理と呼ばれています
-
なお変分原理には、他にもいろいろ知られています
-
光学のフェルマーの原理(光の到達時間最小、光路長最小)
-
測地線(曲面上の最短経路)
-
その他電磁気学のラグランジアン、一般相対論のラグランジアン、などなど
ラグランジアン
エネルギーの次元をもつ以下の量を表す関数をラグランジアンといいます。ここで x は粒子の位置座標、 v は速度。
$$
\begin{eqnarray}
L(x, v) &=& \mathbf{運動エネルギー - ポテンシャルエネルギー} \\
&=& \frac{1}{2} M v^2 - U(x) \hspace{3em} (1)
\end{eqnarray}
$$
例えば、質量 $M$ バネ定数 $K$ の振動子のラグランジアンは以下になります。
$$
L_{oscillator}(x, v) = \frac{1}{2} M v^2 - \frac{1}{2} K x^2 \hspace{3em} (1')
$$
作用積分
あるラグランジアンに対して、以下の形の時間積分を作用あるいは作用積分といいます。
$$
S[x(t)] = \int_{t0}^{t1} L(x(t), \dot{x}(t)) dt \hspace{3em} (2) \\
ただし \ \dot{x}(t) = \dfrac{d x(t)}{dt}
$$
ここで、t0, t1 は任意に固定した時刻、$x(t)$ は粒子の位置を表す 任意の関数 です。
$S$ は任意の関数 $x(t)$ を変数とする関数、すなわち汎関数で、汎関数であることを示すために、$S[x(t)]$ と書きます。
最小作用の原理
上の作用積分 $S[x(t)]$ の変数 x(t) は任意の関数でよいのですが、
$S[x(t)]$ を最小にするような関数が実際に起こる運動 となることが知られています(正しくは「最小」でなく「停留」)
このための必要条件は、関数 $x(t)$ を少し変化させた関数 $x(t) + \delta x(t)$ に対して、$S$ が変化しないこと、すなわち以下で表せます。
$$
\delta S[x(t)] = S[x(t) + \delta x(t)] - S[x(t)] = 0 \hspace{3em} (3)
$$
ただし 境界条件 として、積分の両端では値が変わらないとします。すなわち
$$\delta x(t0) = \delta x(t1) = 0 \hspace{3em} (4)
$$
プログラム
通常は作用積分の停留条件から得られるオイラー・ラグランジュの方程式(2階の微分方程式)を解いて実際の運動を求めるのですが、
ここでは上の作用積分 $S[x(t)]$ を数値的に求める javascript を作成し、$x(t)$ を変化させて $S[x(t)]$ の変化を調べてみます。
振動子のラグランジアン
以下は、質量 M, バネ定数 K の振動子のラグランジアン $L(x,v)$ (1') を作成して返します。
function oscillator(M,K) {
return function(x,v) {
return 0.5*(M*v*v - K*x*x);
};
}
数値微分演算子
以下はきざみ幅 dt で、与えられた関数を数値微分する微分演算子を作成します。
(2) 式の微分を計算するのに使います。
function D_t(dt) {
return function(func_t) {
return function(t) {
return (func_t(t + 0.5*dt) - func_t(t - 0.5*dt)) / dt;
};
};
}
D_t(dt)(func) は関数 func の数値微分を表す関数(すなわち数値導関数)を返します。
(これも関数を変数にとる関数だが、通常、値・数値を返す関数を 汎関数、
別の関数を返す関数は 演算子あるいは作用素 というようです)
グラフプロット
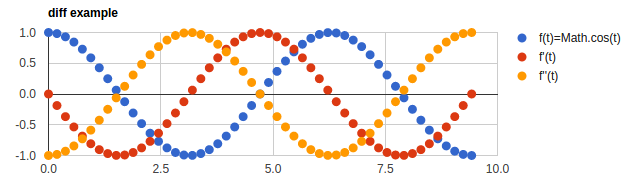
テストをかねて、cos(x) とその1次微分、2次微分をプロットしてみます。
var d_t = D_t(0.0001); // 数値微分演算子
var f = Math.cos; // 微分する関数
var df = d_t(f); // その導関数
var ddf = d_t(d_t(f)); // 2次の導関数
グラフを描くには、x 軸の値が決まれば y 軸の値は上の「関数」で計算できます。このためには x 軸の値を生成する es6 の Generator がぴったり です。
// t0 から dt ごとに t1 まで、順次値を返すイテレータを作成
function* rangeGenerator(t0, t1, dt) {
for(var t = t0; t <= t1; t+= dt) {
yield t;
}
}
グラフは google visualization chart を使いました。
以下でグラフデータを作成します。
/**
* google chart 用のデータ行を作成。
* funcs は1変数関数の配列。先頭は x 軸の値を順次返すイテレータであること。
*/
function chartRows(funcs) {
var rows = [];
for(var t of funcs[0]) {
var row = [];
row.push(t);
for(var i=1; i < funcs.length; i++) {
var val = funcs[i](t);
row.push(val);
}
rows.push(row);
}
return rows;
}
実際にグラフを描くのは以下のような感じです。
以下でX軸値を range = [0, 1.5, 2, 3] などと適当な値の配列にすることもできます。
var d_t = D_t(0.0001); // 微分演算子
var range = rangeGenerator(0, 3*Math.PI, 3*Math.PI/50); // X軸の値のイテレータ
var funcs = [range, Math.cos, d_t(Math.cos), d_t(d_t(Math.cos)]; // X軸値、元の関数、その一次微分、二次微分を返す関数の配列
// チャートデータ作成
var data = new google.visualization.DataTable();
data.addRows(chartRows(funcs)) ;
// 描画実行
var elchat; // 描画先の HTML 要素
var options = {width:500}; // チャートオプション
var chart = new google.visualization.ScatterChart(elchart);
chart.draw(data, options);
描いてみたグラフです。なおグラフの見出しや項目ラベルをつけるなど、少しお化粧しています。
数値定積分演算子
(2)式の作用積分を計算するため、区間 [t0, t1] を分割数 ndiv で数値積分する数値定積分演算子を作成します。
function Int_t(t0, t1, ndiv) {
var dt = (t1 - t0)/ndiv;
return function(func_t) {
var t = t0 + 0.5*dt;
var s = 0.0;
for (var i = 0; i < ndiv; i++) {
s += func_t(t);
t += dt;
}
return s * dt;
};
}
作用積分
与えられた lagrangian(関数)に対して、作用積分汎関数 $S[x(t)]$ を作成します。
int_t は上の定積分演算子、d_t は上の微分演算子です。
被積分関数とともに、数値計算用の演算子を渡すのがみそ です。
function ActionIntegral(int_t, d_t, lagrangian) {
return function(xt) {
var dxdt = d_t(xt);
var func_t = function(t) {
return lagrangian(xt(t), dxdt(t));
};
return int_t(func_t);
};
}
トライアル
準備ができたので、試行関数 $x(t)$ をいろいろ変えて $S[x(t)]$ の変化を調べてみます。
$x(t)$ は 任意の関数 ですが、もちろんそんなことはできないので、いくつかのパラメータで $x(t)$ を表し、パラメータを変化させてみることになります。
ここではごくごく単純に 1つのパラメータ w を持つ以下を試行関数にして、以下の条件で調べてみます。
- ラグランジアン: 上の振動子のものを使用
- 解析解は $x(t) = A sin(\omega t) + B cos(\omega t)$ ($\omega = \sqrt{K/M}, A, B は定数$)
- 積分範囲: $[t_0, t_1]=[0,1]$
- 境界条件:$x(t0)=0、x(t1)=1$
- 試行関数:簡単のため、ここでは角周波数 w をパラメータとして解析解と同じサイン・コサインで表します。上の境界条件から以下とします
- $x(t;w) = sin(wt)/sin(w t_1)$
function trialFunc(t, w) {
return Math.sin(w*t)/Math.sin(w*t1);
}
実行結果
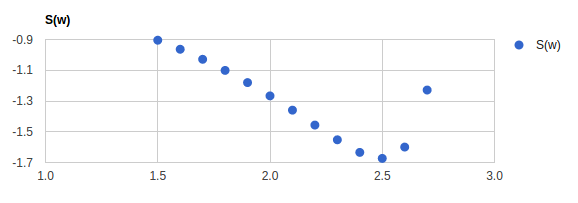
以下 $M=1.0,\ K=2.5^2$ として、試行関数のパラメータ $w=1.0 ~ 3.0$ の範囲で、作用積分 $S(w)$ をプロットしてみた結果です。ちゃんと正解の $w=2.5$ あたりで最小になっているようです。
不思議といえば不思議ですね。。。
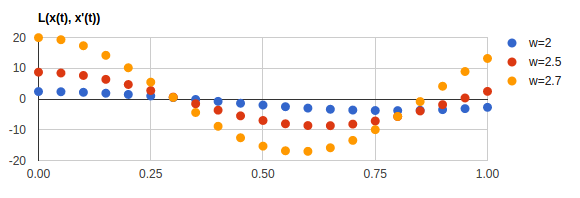
ついでに、いくつかのパラメータ $w$ における被積分関数=ラグランジアンの時間変化をプロットしていみました。 こんな感じになるみたいです。
まとめ
javascript で変分問題を数値的にプログラムしてみました。
例題や試行関数があまりに単純なので、実用的価値はまったくないですが。。。
結果的に、全部 javascript のクロージャで書いてしまいました。
これでいいのかどうかはよく分からないんだけど、個人的にはこんなものかと。(ぜひご指導ください)
- (あたりまえですが)javascript での関数プログラミングやクロージャは十分実用的
- 関数プログラミングは、関数を作ってそれを返す関数を作る、という感じになりますが、少し慣れるとわりと簡単です。でもその後や人のコードなどはどうしても分かりにくくなる傾向があると思います
- 面倒でもちゃんとコメントをつけるとか、書き方を工夫するなどしたほうがよいかも
- es6 の「アロー関数」を使うと多少とも分かりやすくなるかも。そのうち全部 es6 で書き直してみたいと思います
また例題とした「古典力学のラグランジアン」とかよりも、測地線(曲面上の最短経路)などのほうが一般的でわかりやすかったかも。ただ絵をかくなど大変そうだったので、今回は手抜きしました。
汚いですが、作成したプログラム一式はこちら html javascript
参考(になる? ならない?)文献
- 物理や数学というよりは、変分原理の哲学・神学的な歴史についてのお話しが主
- わりと面白いような気もするし、つまらないような気もする。びみょう~
- 付録に多少数学的なシンプレクティック幾何学などの解説がある