概要
フーコーの振り子の動き(振動面が回転する様子)を体感する? 簡単な紙細工とGIFアニメを作ってみました。
紙細工の作り方

- 画像を印刷、紙を太線で切り抜いて、まんなかの開いた円板を作る
- 0°の左の太線にもハサミを入れる
- 0°の線を例えば 50°の破線の上に重なるように紙を曲げて、クリップなどで固定する。上部を切り取った円錐面ができる
- 目盛は緯度(北緯)を示す。緯度をかえて試してみてください
- まんなかが開いているのは単に曲げやすくするためです
| 組み立て | 完成写真 |
|---|---|
 |
 |
(あんまり面白くないけど)見方・遊び方
静止系から見た動き
作った円錐の上部(北)を上から見て、左回り(西から東)で順に矢印を見ていきます。
緯度 = 50°では一周すると、矢印は左回りに約90°回転することが分かります。
- 正確には $2 \pi (1-sin(緯度)) ラジアン$ で 84.2°
- なお一周したあとは、上にある0°の面でなくて下に隠れている面に続きます(すぐ終わっちゃうけど)
これが静止系から見たフーコーの振り子の回転の様子です。
みかけの動き
こんどは円錐を固定し、自分が**左回り(西から東)に回りながら、正面にくる矢印を見ていきます。
(不精な方は、自分は動かずに円錐を右回り(東から西)**に回して、正面にくる矢印を見ていく)
緯度 = 50°では一周すると、矢印は右回りに約270°回転することが分かります。
- 正確には $- 2 \pi sin(緯度) ラジアン$ で -275.8° (マイナスは右回りを示す)
- ちなみに、フーコーの振り子の公開実験が行われたパリの緯度は北緯48度51分44秒
これが地表に固定された観測者から見たときのフーコーの振り子の回転の様子、すなわちみかけの動きです。
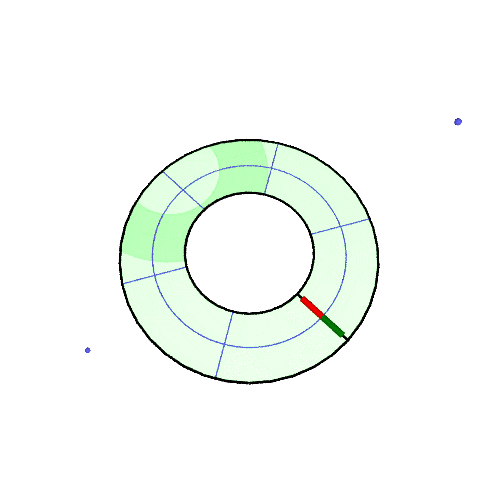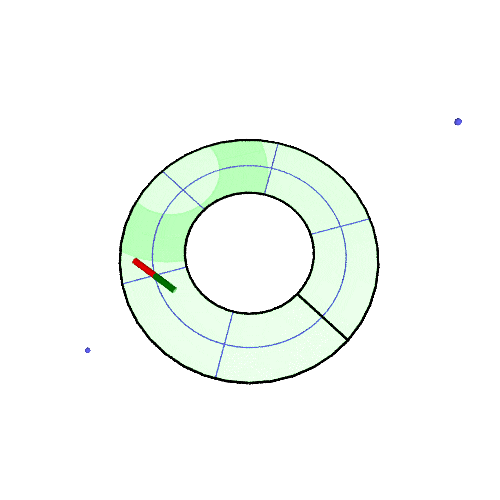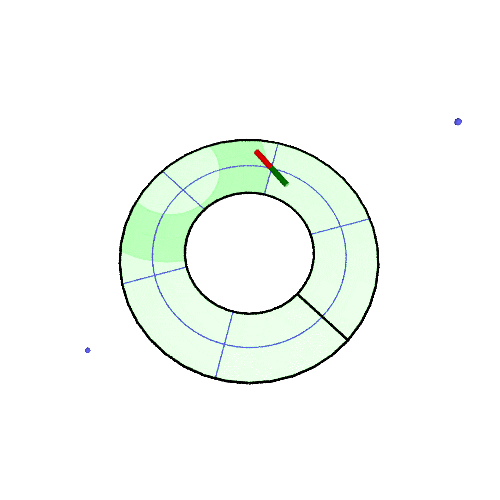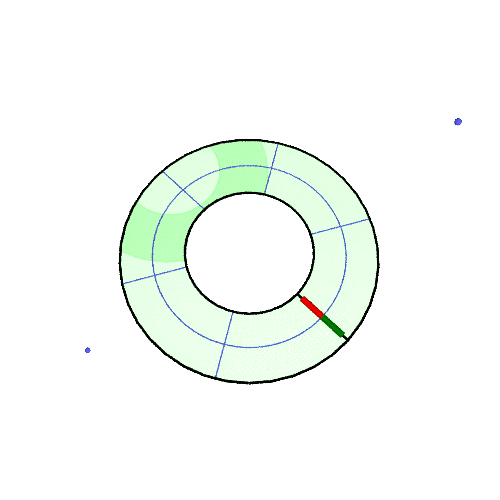
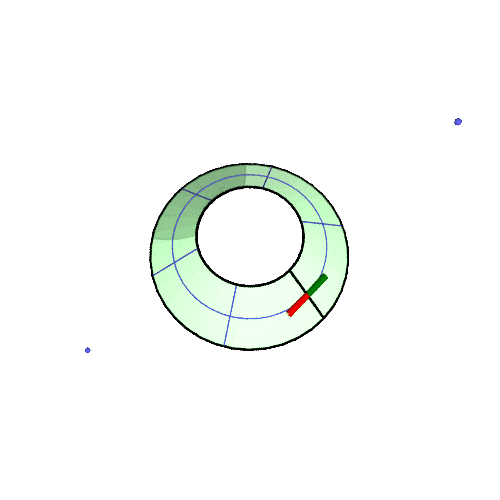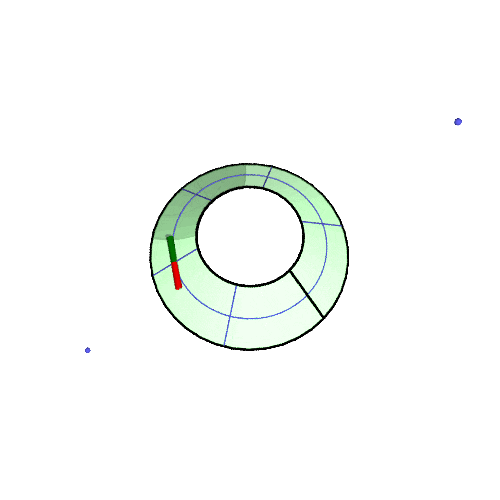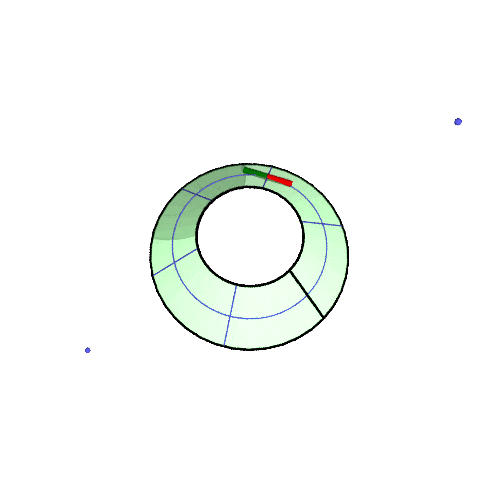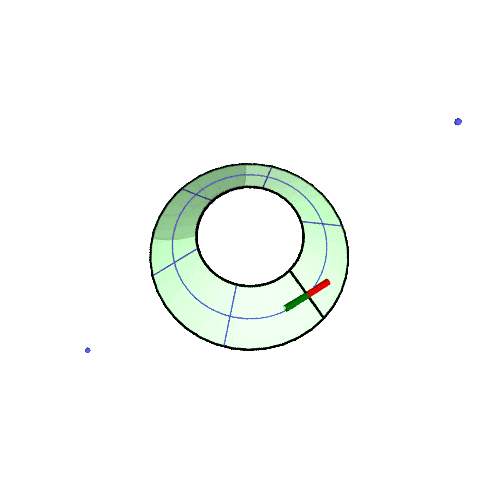
3D アニメ
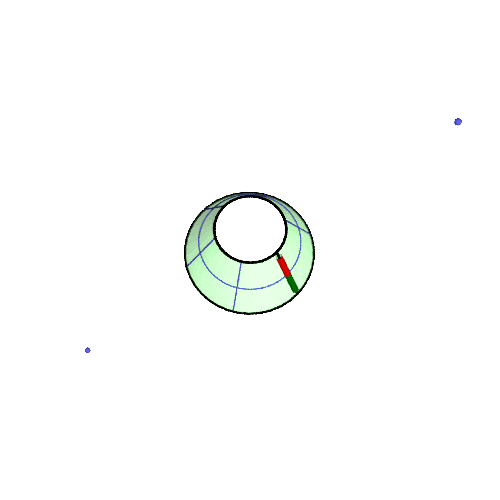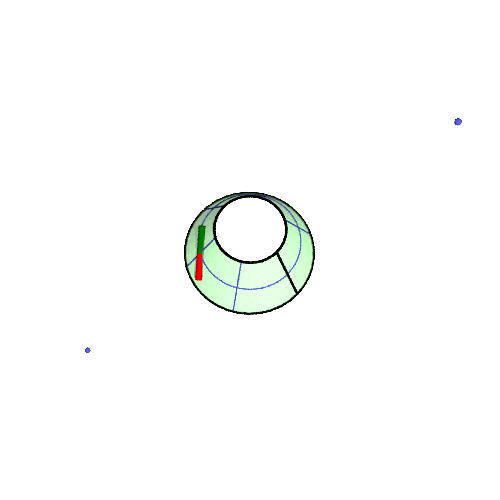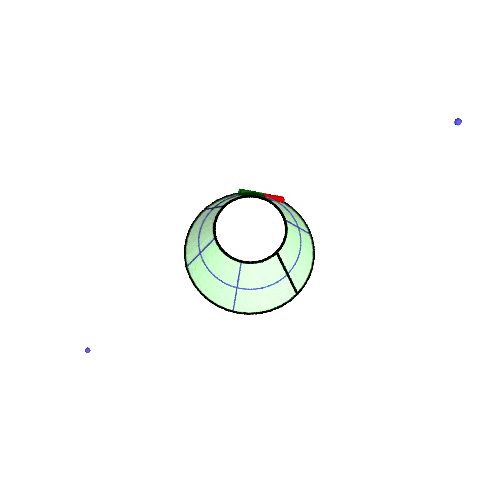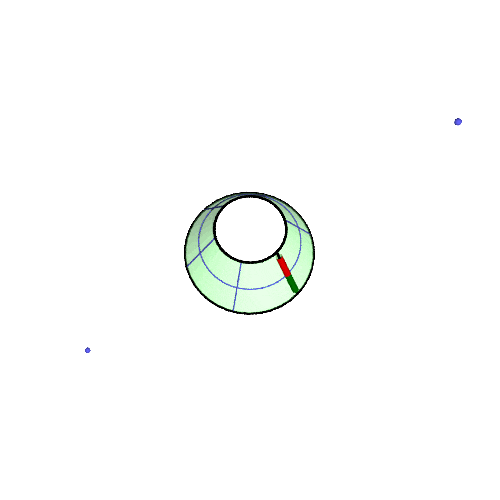
北緯50°での振り子の回転の様子の GIF アニメです。(描画は2周だけ、あとは繰り返しなので境目で不連続になる)

アニメが止まっている場合は「画像だけを別タブ/ウインドウに表示」して、リロードしてみてください。
説明
緯度=90°(北極) の場合
- 北極では地面は地軸と直交した平面内で回転する
- 慣性により振動面の向きが保たれるので、振り子は静止系に対しては回転せず、
- 単に平行移動 する
一般の緯度の場合
- 一般の緯度では、地面は地軸に対して一定の角度(90° - 緯度)だけ傾いて地軸のまわりを回転する
- 従って振り子は円錐面内で動いていく

- 振り子はこの円錐面内で 平行移動 していく、と考えられる
- もちろん力学的な現象であるフーコーの振り子の動きと、数学・微分幾何学でいう平行移動 が対応するかは検証する必要がありますが、それはまたの機会に。。。
でも 曲面上の平行移動 は難しい
- 曲面上の平行移動は、移動させる経路に依存する
- 測地線とか共変微分とか接続とか。。。
でも、実は円錐面は曲がっていない!
- 円錐面は平面に展開できる(可展面というらしい、要するにガウス曲率 0)
- というわけで、矢印を展開図(扇形)上で平行移動させて、それを円錐面に変換したのが上の紙細工とアニメです
| 扇形上で平行移動 | それを円錐にすると | |
|---|---|---|
| 50° | 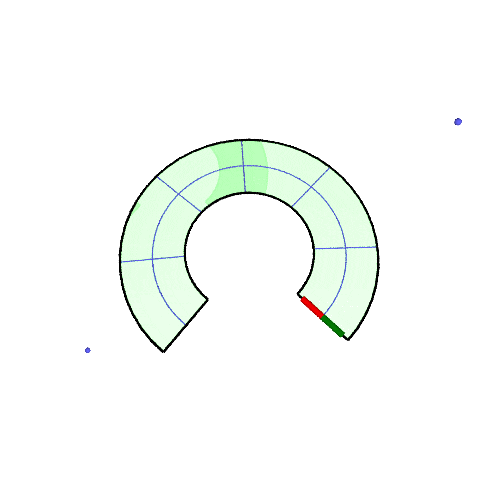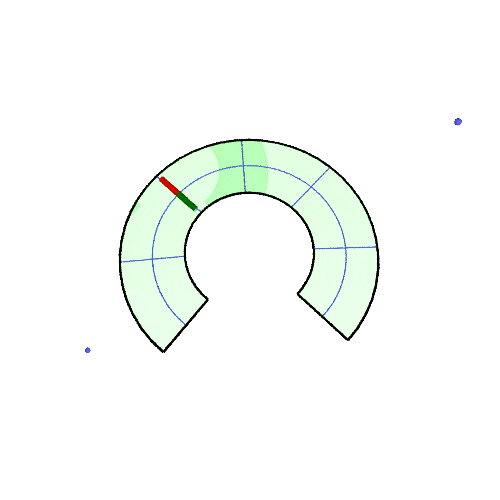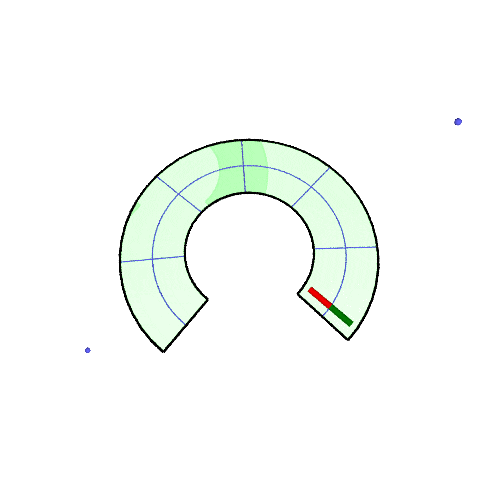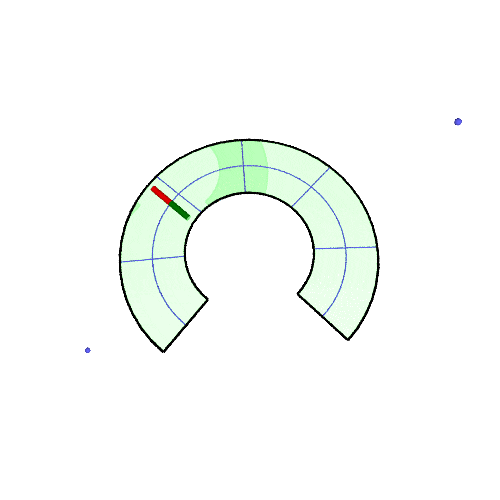 |
 |
| 30° | 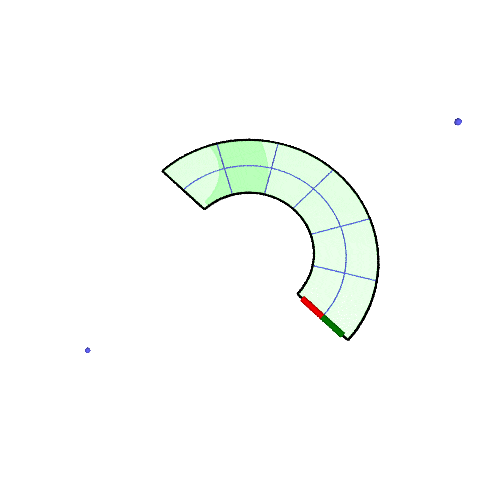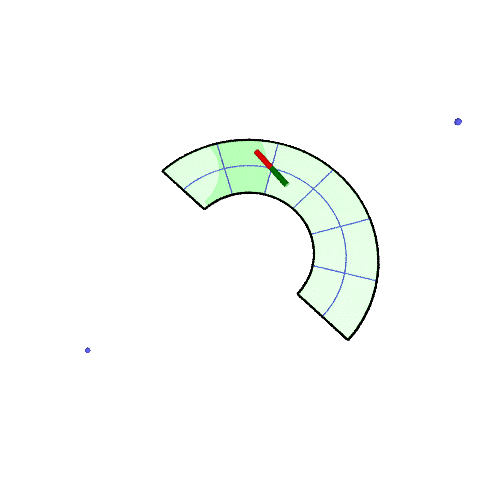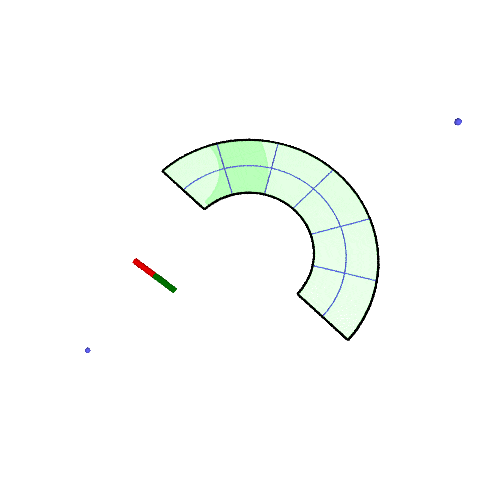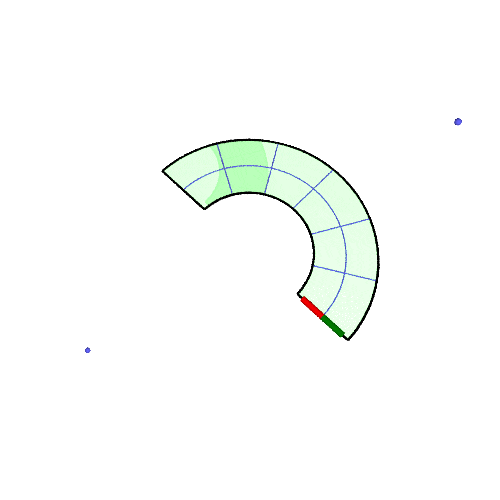 |
 |
扇形・円錐面変換
上の紙細工は以下のように、平たい扇形から円錐面への変換(変形)をやっていることになります。
- 扇形の半径を $R$、中心角を $\Theta$
- これを絞ってできる円錐 の底面の中心角を $\Theta' (> \Theta)$ とする
- $\Theta'=2 \pi$ のときちょうど隙間のない円錐面になる
- 扇形上の点の極座標を $(r,\theta)$
- それに対応する円錐面上の点を円柱座標で $(r', \theta', z')$
とすると
- $a = \Theta/\Theta' (< 1)$
- $r' = a r$
- $\theta' = \theta / a$
- $z' = (R - r) \sqrt{1 - a^2}$
この変換は等長変換(長さも角度も変えない変換、伸縮のない変換)なので、扇形状の平行線は円錐面上の平行線に変換されることになります。
To Do:(いつになるか分からへんけど)続編予定
- 角度欠損(デカルトの不足角の定理)とガウス・ボネの定理(数学)
- 角度・角速度ベクトル(力学)
- フーコーの振り子 or ジャイロスコープの運動(力学)
参考
- en.wikipedia "Foucault pendulum"
- Oprea, John (1995). "Geometry and the Foucault Pendulum" . Amer. Math. Monthly 102: 515–522.
- これは上の最初の Reference だけど 球面 で説明している
- でも基本的な理解には 円錐面 で十分、微分も積分も不要なのだ
蛇足
図とアニメは sage で作りました。
sage も python も初心者で、まだいろいろ分からない。。。
- 3Dアニメで view point を回転するのはどうすりゃいいの ??
- やむなくモデルのほうを回転したが、今度は回転でサイズが変わってしまう
- しなたないので、フレームサイズを固定するために2点を追加して描画。。。
- やむなくモデルのほうを回転したが、今度は回転でサイズが変わってしまう
- アニメの
外枠(frame) が取れない、奥の円錐面にへんな影。。。なんでやろ?
なおこのアニメには、実はまだ微妙なバグがあって。。。
- 振り子の最初の向きを「横向き」にすると、へんな動きをします
- 原因は苦労の上分かったけど、どう直すか悩み中。。

(原因)
- 平行移動した線分を描くために、以前は2点を展開図上の x,y 座標で求め、それを $r, \theta$ にして円錐面上の2点を求めていた
- これだと $\theta$ を求めるのに arc tangent など必要で、どこかで位相 $\theta$ が $2 \pi$ だけ飛んでしまう
- ところが $\theta$ の周期は $2 \pi$ だが、$\theta'$ の周期は $2 \pi/a$ なので、ときどきおかしくなっていた
(修正)
- 2点の x,y 座標でなく、円錐面上の接ベクトルで線分を描くように修正。接ベクトルの計算は sage 君がやってくれる
- それくらい手で計算しなよな、簡単なんだから。ボケるぞ!
# 円錐面上の線分の plot を得る。 r, len, phiを一定にして th を変化させると緯度上を平行移動した線分が得られる
# surf: 円錐面の ParametrizedSurface3D
# r, th: 平面上の極座標での位置
# len, phi: 線分の長さの半分と、線分とX軸とのなす角度
def pline(self, surf, r, th, len, phi, **args):
at = (r,th) # 平面上の極座標での位置ベクトル
dir = (cos(phi-th), sin(phi-th)) # 平面上の極座標での phi方向のベクトル
t1 = surf.tangent_vector(at, dir) # 円錐面の接ベクトルの (x,y,z) 座標
t1 = t1 / abs(t1) # 規格化
p0 = self.xyz0(at) # 中心点の (x,y,z) 座標
p1 = p0 + len*t1 # 線分の開始点
p2 = p0 - len*t1 # 線分の終了点
t = var('t')
eq = p1*t + p2*(1-t) # (x,y,z) 座標での線分の方程式
a = parametric_plot3d(eq, (0,0.5), color='red', thickness=5, **args)
b = parametric_plot3d(eq, (0.5,1), color='green', thickness=5, **args)
return a+b;