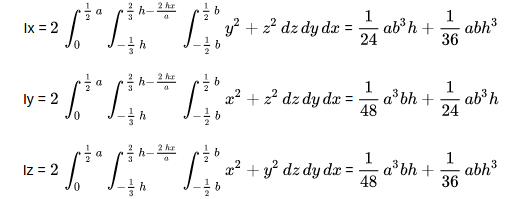二等辺三角形の薄い板の 慣性モーメント を計算してみました。
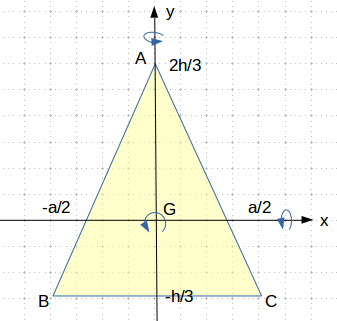
二等辺三角形の底辺の長さを $a$, 高さを $h$, 面密度は $\sigma$ で一定とします。
二等辺三角形の重心 G を原点とします。
$x,y,z$ 軸まわりの各慣性モーメントは、
$$
I_{x} = \int_{三角形} \sigma y^2 dxdy \\
I_{y} = \int_{三角形} \sigma x^2 dxdy \\
I_{z} = \int_{三角形} \sigma (x^2+y^2) dxdy
$$
ここでは以下の慣性モーメントの性質を使って、積分せずに計算してみます。
(もちろんこれらの性質は、上の積分を用いた定義から得られます)
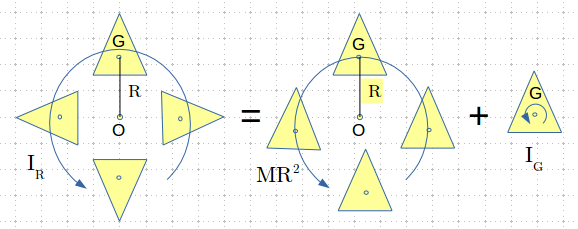
性質1:重心を通らない軸のまわりの慣性モーメント
物体の重心を通る軸まわりの慣性モーメントを $I_G$、全質量を $M$ とすると、その軸を距離 $R$ だけ平行移動した軸まわりの慣性モーメント $I_R$ は以下になる。
$$ I_{R} = M R^2 + I_{G} $$
すなわち、自転せずに全質量 $M$ が回転するときの慣性モーメントと、重心まわりに自転するときの慣性モーメントの和になる。
性質2:相似な物体の慣性モーメント
均質な物体のサイズを $\alpha$ 倍した物体の重心まわりの慣性モーメントは、元の $\alpha^{5}$ 倍になる。
(ただし今の場合厚さ=0 としているので、$\alpha^{4}$ 倍になる)
計算
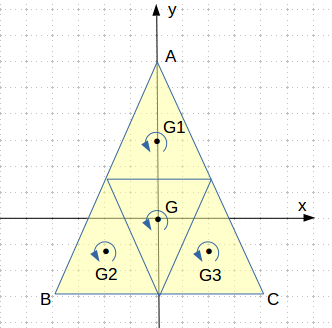
各辺の中点を結んで、以下のように4つの相似な三角形に分割します。
これらは全体を 1/2 に縮小したものになっています。
各小三角形の重心の座標は
$$
G=(0,0),\ G_1=(0,h/3),\ G_2=(-a/4,-h/6),\ G_3=(a/4,-h/6)
$$
まず $I_z$ を求めてみる。
小さい三角形は元の 1/2 倍なのでその重心まわりの慣性モーメントは $I_z / 2^4$, 面積は元の 1/4 なので質量は $\sigma ah/8$。従って
$$
I_z = (\frac{\sigma ah}{8} \times \overline{GG}^2 + \frac{I_z}{16} )
- (\frac{\sigma ah}{8} \times \overline{GG_1}^2 + \frac{I_z}{16} )\\
- 2 \times (\frac{\sigma ah}{8} \times \overline{GG_2}^2 + \frac{I_z}{16} ) \\
$$
同様に
$$
I_x = (\frac{\sigma ah}{8} \times 0^2 + \frac{I_x}{16})
- (\frac{\sigma ah}{8} \times (h/3)^2 + \frac{I_x}{16} )\\
- 2 \times (\frac{\sigma ah}{8} \times (h/6)^2 + \frac{I_x}{16} ) \\
I_y = 2 \times (\frac{\sigma ah}{8} \times 0^2 + \frac{I_y}{16}) - 2 \times (\frac{\sigma ah}{8} \times (a/4)^2 + \frac{I_y}{16} ) \\
$$
全体の質量 $M = \sigma ah/2$ なので、これらより以下が得られる。
$$
I_x = \frac{\sigma a h^3}{36} = \frac{M h^2}{18} \\
I_y = \frac{\sigma a^3 h}{48} = \frac{M a^2}{24} \\
I_z = \sigma ah (\frac{a^2}{48} + \frac{h^2}{36})
= M (\frac{a^2}{24} + \frac{h^2}{18})
$$
なお $I_z = I_x + I_y$ から計算してもよい。
特に正三角形の場合は $h=\sqrt{3}a/2$ だから以下となる。
$$
I_x = I_y = \frac{\sqrt{3} \sigma a^4}{96}
= \frac{\sqrt{3}M a^2}{48} \
I_z = 2 I_x
$$
正三角形さらに一般の正多角形の場合、重心を通る面内の任意の軸は主軸となり、そのまわりの慣性モーメントは等しい。
厚さを考慮した場合
上では厚さ=0 としたが、厚さを b、密度を $\rho$ とすると、同様に計算して以下になる。
$$
I_x = \rho abh (\frac{h^2}{36} + \frac{b^2}{24}) = M (\frac{h^2}{18} + \frac{b^2}{12})\\
I_y = \rho abh (\frac{a^2}{48} + \frac{b^2}{24}) = M (\frac{a^2}{24} + \frac{b^2}{12})\\
I_z = \rho abh(\frac{a^2}{48}+\frac{h^2}{36}) = M (\frac{a^2}{24}+\frac{h^2}{18})
$$
$a^2,h^2,b^2$ の係数の分母の比が $4:3:2$ となるようである。
なおチェックのため、sage君に積分を計算してもらった。
from sage.symbolic.integration.integral import definite_integral
var('x,y,z, a,h,b')
def trimom(name, func, a, h, b):
iz = definite_integral(func,z,-b/2,b/2, hold=True)
iy = definite_integral(iz, y, -h/3, -2*h*x/a+2*h/3, hold=True)
ix = 2* definite_integral(iy, x, 0, a/2, hold=True)
show(name, "=", ix, "=" , ix.simplify().expand())
return ix
Ix = trimom("Ix", (y^2+z^2), a, h, b)
Iy = trimom("Iy", (x^2+z^2), a, h, b)
Iz = trimom("Iz", (x^2+y^2), a, h, b)