精密農業に向けた勉強記事です。
精密農業とは、土地を分析して農地の肥沃度等を明らかにし、効率的に収益を上げる農業のことです。
土地分析の地力(肥沃度)分析に機械学習を使用し、その結果から地力(肥沃度)マップを作成する予定です。
この記事ではその中で機械学習について取り扱います。
本番では特定のポイントの要素(土地成分等)に基づきクラスタリング、地力をレベル分類し、そのクラスタリング結果をもとにポイント間の地力を分析、解明します。
今回は勉強として、サンプルデータをpython(Google Colaboratry)の環境で機械学習の教師なし学習(k-means法)を用いてクラスタリングすることを目指します。
この記事の流れ
以下の流れで進行します。
- 必要拡張モジュール等のインポート
- 使用データセットの読み込み
- データ整理
- データの標準化
- 相関係数の確認
- 主成分分析
- k-means法によるクラスタリング
- シルエット分析
- バイプロット図
1. 必要拡張モジュール等のインポート
使用するモジュールをインポートします。
import pandas as pd
import numpy as np
import csv
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples
from matplotlib import cm
<使用モジュールの役割>
pandas→データ解析
numpy→データ整理
csv→csvファイル読み込み
sklearn→k-means法ライブラリ
seaborn→相関係数可視化
matplotlib→グラフ可視化
2. 使用データセットの読み込み
本記事ではUC Irvine Machine Learning RepositoryのSeedsデータセットを使用します。
UC Irvine Machine Learning Repository Seeds
df=pd.read_csv("seeds_dataset.csv",header=None)
3. データ整理
読み込んだデータセットで、7,8,9列目は本記事では機械学習に使用しないため削除します。
また、Nanが含まれる行の削除も行い、データを整理します。
df.drop(df.columns[[7,8,9]],axis=1,inplace=True) #7,8,9列目の削除
df.dropna(how='any',inplace=True) #Nanが含まれる行の削除
df.to_csv('seeds_dataset2.csv') #今後使用しやすいように整理したデータを保存
4. データの標準化
k-means法を行う際はデータの標準化を行う必要があります。
k-means法ではデータ点同士の距離を用いるため、一つのデータの絶対値が大きい場合、同じ分散でもデータ点同士の距離が大きくなり、クラスタ分類の計算に影響を与えてしまいます。
そのため、標準化を行って事前にデータの大きさを揃えておきます。
scaler=StandardScaler() #標準化を行う関数StandardScalerをscalerという名前に定義
dfs=scaler.fit_transform(df) #データであるdfを標準化
5. 相関係数の確認
データの相関係数を見ることで相関の強いデータを見分けます。
相関が強いデータは似ているため使用するか検討を行います。今回はそのまま使用しました。
corrs = np.corrcoef(dfs,rowvar=False) #相関係数の計算
sns.heatmap(corrs, cmap=sns.color_palette('Reds', 10)) #ヒートマップで可視化
結果
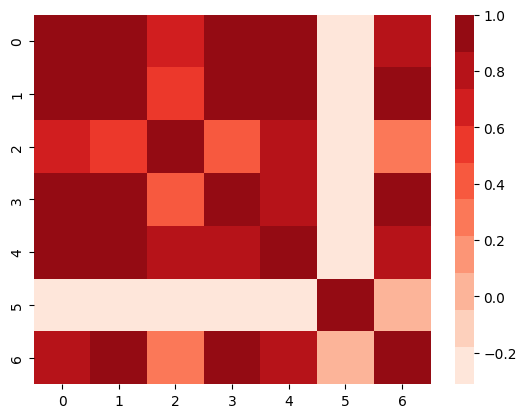
0,1,3,4の相関が高いように見えます。今回はすべて使用しますが、抽出してもいいかもしれません。
6. 主成分分析
主成分分析を行い、主成分ごとの寄与率、累積寄与率を見ることで使用する主成分のみを抜き出し、機械学習に用います。
すべての主成分を用いて機械学習を行うと予測精度の低下や過学習が起きるかもしれないため、使用する主成分を抽出します。
pca=PCA()
pca.fit(dfs) #主成分分析
ev = pd.DataFrame(pca.explained_variance_ratio_) #寄与率
t_ev = pd.DataFrame(pca.explained_variance_ratio_.cumsum()) #累積寄与率
#可視化に用いる変数定義
length=7
kiyoritu=ev*100
ruiseki=t_ev*100
xlab=np.array([1,2,3,4,5,6,7])
# サイズ指定
fig = plt.figure()
# 軸関係の表示
ax = fig.add_subplot(111)
# データ数のカウント
data_num=length
# 棒グラフの描画
ax.bar(range(data_num), kiyoritu[0])
ax.set_xticks(range(data_num))
ax.set_xticklabels(xlab)
ax.set_ylim([0,100])
# 折れ線グラフの描画
ax_add = ax.twinx()
ax_add.plot(range(data_num), ruiseki[0])
ax_add.set_ylim([0, 100])
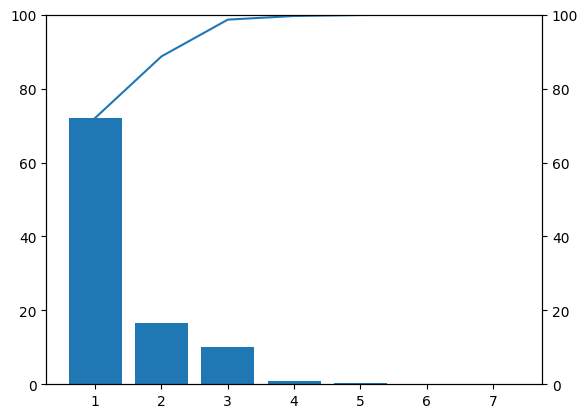
棒グラフが寄与率、折れ線グラフが累積寄与率を表しています。
このグラフから第二主成分までで累積寄与率が80%を超えていることがわかるため、本記事では第二主成分までを用いて機械学習を行いました。
第二主成分までを用いることにしたためデータの抽出を行う必要があります。
pcs=pca.transform(dfs) #転置
pcs2=pcs[:,:2] #2列目までを抽出(第二主成分までを抽出)
7. k-means法によるクラスタリング
ここまでデータを整理し、抽出してきました。
このデータにk-means法を用いてクラスタリングを行います。
また、この結果を可視化します。
km = KMeans(n_clusters=3, # クラスターの個数 # セントロイドの初期値をランダムに設定 default: 'k-means++'
n_init=10, # 異なるセントロイドの初期値を用いたk-meansの実行回数 default: '10' 実行したうちもっとSSE値が小さいモデルを最終モデルとして選択
max_iter=300, # k-meansアルゴリズムの内部の最大イテレーション回数 default: '300'
tol=1e-04, # 収束と判定するための相対的な許容誤差 default: '1e-04'
random_state=0) # セントロイドの初期化に用いる乱数発生器の状態
cluster = km.fit_predict(pcs2) #クラスタリング
plt.scatter(pcs2[cluster==0,0], # cluster(クラスター番号)が0の時にpcs2の0列目を抽出
pcs2[cluster==0,1], # cluster(クラスター番号)が0の時にpcs2の1列目を抽出
s=50,
label='cluster 1')
plt.scatter(pcs2[cluster==1,0],
pcs2[cluster==1,1],
s=50,
label='cluster 2')
plt.scatter(pcs2[cluster==2,0],
pcs2[cluster==2,1],
s=50,
label='cluster 3')
plt.legend() #凡例
plt.grid() #グリッド線
plt.show()
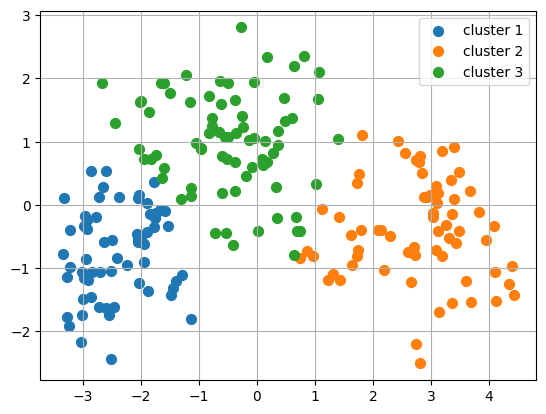
第一主成分をx軸、第二主成分をy軸としています。
ここでクラスタリング結果が塊ごとに分散されていればうまくクラスタリングできていると思います。
8. シルエット分析
シルエット分析という手法でこのクラスタリングが本当に信頼できるか分析を行います。
シルエット分析では、以下の4点からクラスタリングがうまくできているか判断します。
・値が1に近いほど性能が高い
・値が負になると、所属クラスタの判別が間違っている可能性あり
・クラスタ内は密に凝集されているほど良い
・異なるクラスタは遠く離れているほど良い
cluster_labels = np.unique(cluster) # clusterの要素の中で重複を無くす
n_clusters=cluster_labels.shape[0] # 配列の長さを返す。つまりここでは n_clustersで指定した3となる
# シルエット係数を計算
silhouette_vals = silhouette_samples(pcs2,cluster,metric='euclidean') # サンプルデータ, クラスター番号、ユークリッド距離でシルエット係数計算
y_ax_lower, y_ax_upper= 0,0
yticks = []
for i,c in enumerate(cluster_labels):
c_silhouette_vals = silhouette_vals[cluster==c] # cluster_labelsには 0,1,2が入っている(enumerateなのでiにも0,1,2が入ってる(たまたま))
c_silhouette_vals.sort()
y_ax_upper += len(c_silhouette_vals) # サンプルの個数をクラスターごとに足し上げてy軸の最大値を決定
color = cm.jet(float(i)/n_clusters) # 色の値を作る
plt.barh(range(y_ax_lower,y_ax_upper), # 水平の棒グラフのを描画(底辺の範囲を指定)
c_silhouette_vals, # 棒の幅(1サンプルを表す)
height=1.0, # 棒の高さ
edgecolor='none', # 棒の端の色
color=color) # 棒の色
yticks.append((y_ax_lower+y_ax_upper)/2) # クラスタラベルの表示位置を追加
y_ax_lower += len(c_silhouette_vals) # 底辺の値に棒の幅を追加
silhouette_avg = np.mean(silhouette_vals) # シルエット係数の平均値
plt.axvline(silhouette_avg,color="red",linestyle="--") # 係数の平均値に破線を引く
plt.yticks(yticks,cluster_labels + 1) # クラスタレベルを表示
plt.ylabel('Cluster')
plt.xlabel('silhouette coefficient')
plt.show()
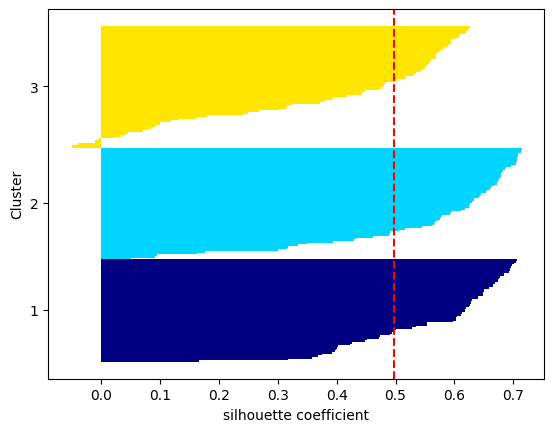
ここではクラスター3が負の値を示す部分がありますが、おおむねうまくいっていると判断しました。
9. バイプロット図
バイプロット図を作成し、各変数の第一主成分、第二主成分における重みを表します。
各変数がどの主成分に大きく影響しているかを確認し、データの分析、整理に使用します。
PC1 = pca.components_[0,:] #第一主成分
PC2 = pca.components_[1,:] #第二主成分
ldngs = pca.components_
scalePC1 = 1.0/(PC1.max() - PC1.min())
scalePC2 = 1.0/(PC2.max() - PC2.min())
features = ["Area","Perimeter","Compactness",
"Length of kernel","Width of kernel","Asymmetry Coeff",
"Length of kernel groove"] #各変数名
fig, ax = plt.subplots(figsize=(14, 9))
for i, feature in enumerate(features):
ax.arrow(0, 0, ldngs[0, i],
ldngs[1, i])
ax.text(ldngs[0, i] * 1.15,
ldngs[1, i] * 1.15,
feature, fontsize=18)
ax.set_xlabel('PC1', fontsize=20)
ax.set_ylabel('PC2', fontsize=20)
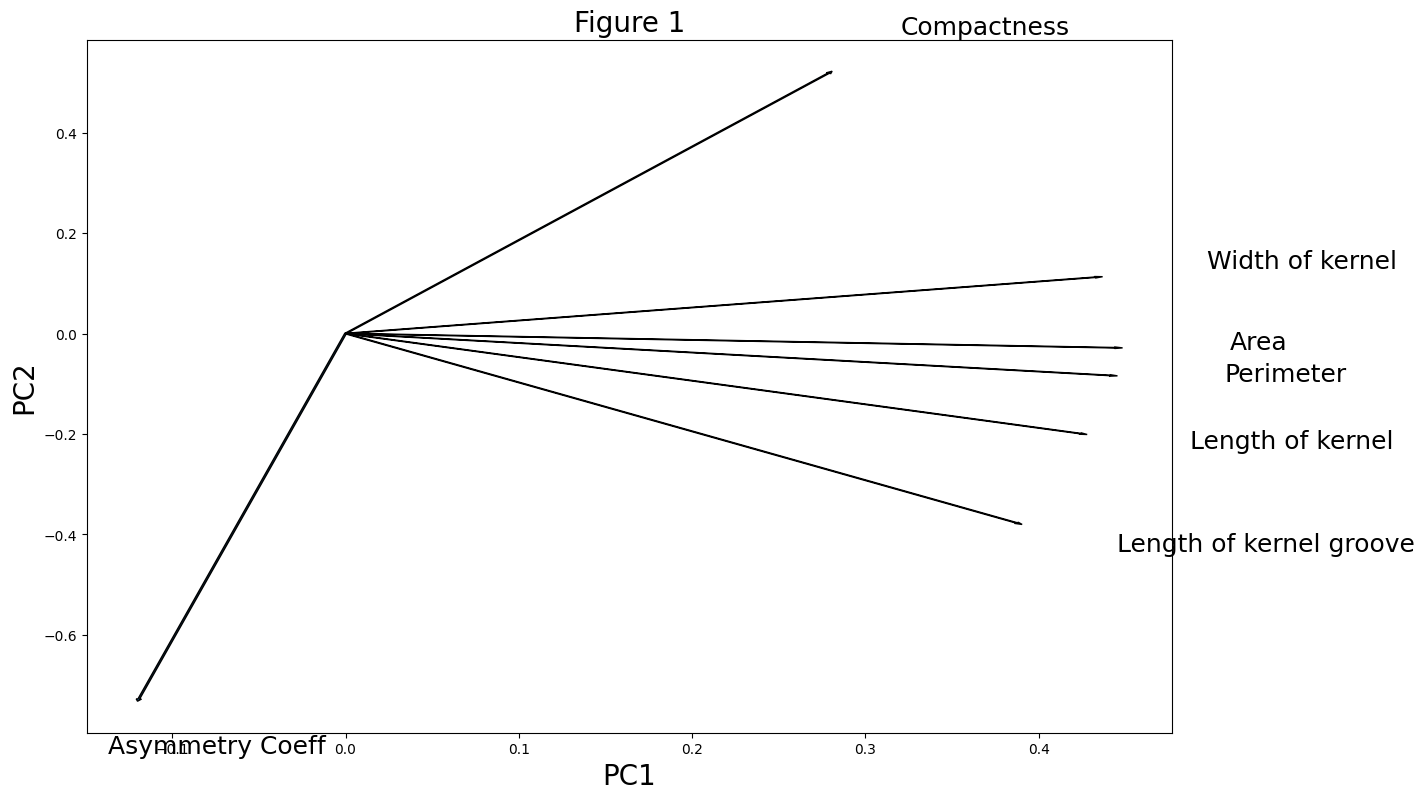
ax.set_title('Figure 1', fontsize=20)
PC1が第一主成分、PC2が第二主成分です。第二主成分はほとんどAsymmetry Coeffが占めているとわかります。
最後に
データを読み込んで整理、分析して整理とデータの整理や抽出が最も重要だと思います。
適切なデータの使用、信頼性の分析を心掛けましょう。
実施予定の精密農業では土地の成分等のデータを今回のように機械学習を使用してクラスタリングし、その結果をもとに地力マップを作成します。
QGISを用いた地力マップの作成を次回以降の記事にしたいと考えています。
よろしくお願いします。