【論文解説】Mixboxで色材の混色を計算する

Mixboxとは

Mixboxは色材(pigments)の混合を効率的に計算する手法およびライブラリです。本記事ではMixboxの論文を解説します。

論文：
Sochorová, Šárka, and Ondřej Jamriška. "Practical pigment mixing for digital painting." ACM Transactions on Graphics (TOG) 40.6 (2021): 1-11.

ソースコード：

モチベーション

青と黄色の絵の具を混ぜると緑になるのは常識ですが、デジタル画の世界では事情が異なります。

以下の図は、GIMP(無料のペインティングツール)で青と緑を混合した結果です。標準モード(左)では灰色、加算モード(右)では白色になりました。どちらも緑色とかけ離れています。

意外なことに既存のペイントツールの多くは、色材の混色を正しくシミュレーションする機能を持ち合わせていません。論文ではその理由として、チャネルの増加に伴う計算負荷の増大やRGBチャネルを基にしたシステムとの不整合が挙げられています。

著者らはRGBチャネルのまま色材の混色を効率的に計算する手法を提案し、上記の問題の解決に取り組みました。

色材の反射率

そもそも色材の色はどのように決まるのでしょうか？

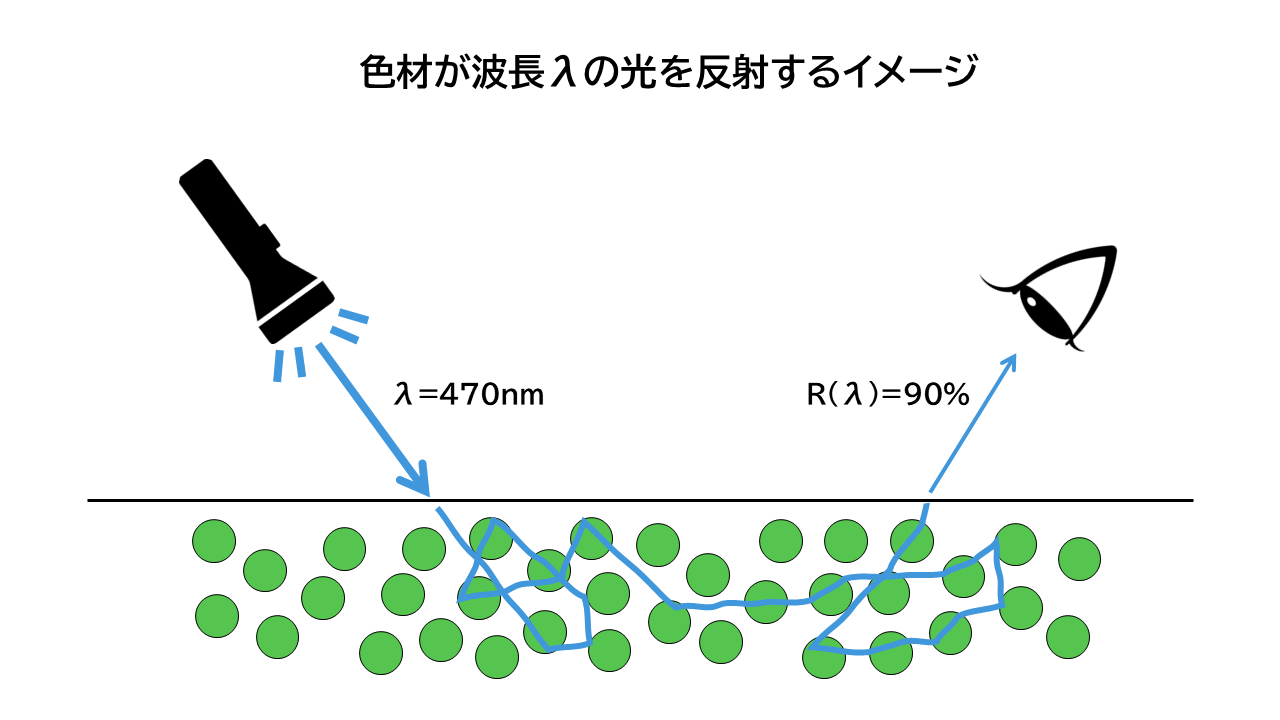
絵具を小さな粒子の集まりと考えてみましょう。粒子は各波長の光を散乱・吸収します。「絵具の色」とは、粒子が他の粒子の反射光を繰り返し散乱・吸収し、最終的に私たちの目に向かって反射した光のことです。

次の図は波長$\lambda$の光を色材が反射する様子を表しており、光の10%を吸収し、90%を反射しています。

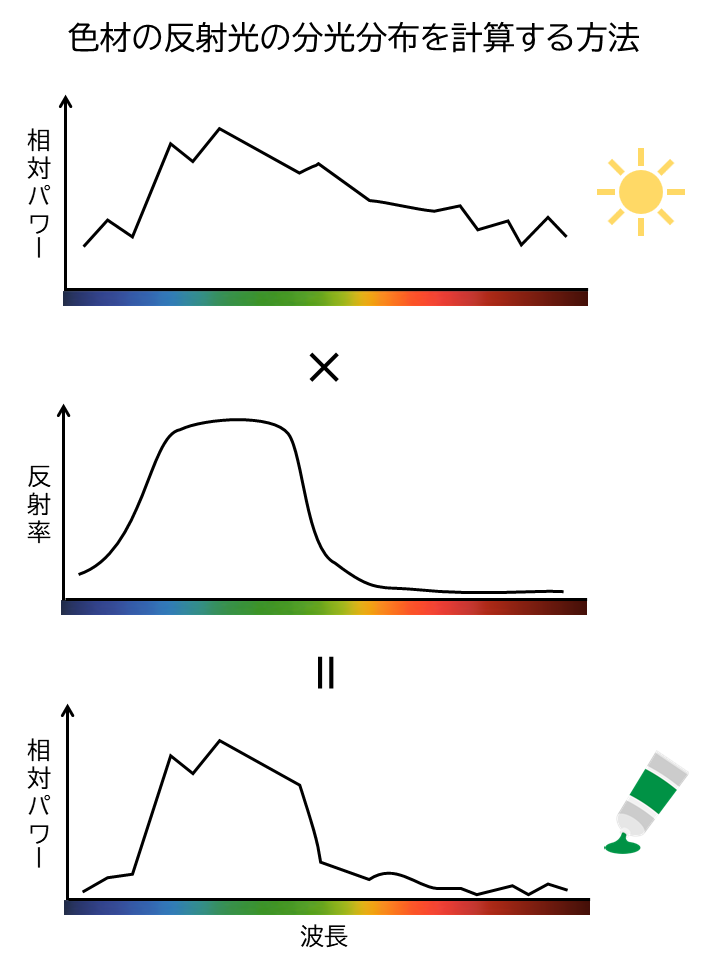
太陽光は赤・黄・緑・青・紫などの単色光から構成され、波長ごとに異なる放射エネルギーを有します。たとえば、標準昼光光源の放射エネルギーの分布（分光分布）$D_{65}(\lambda)$は次の通りです。¹

色材の反射光の分光分布は、光源の分光分布$D(\lambda)$と反射率の分布$R(\lambda)$の積$D(\lambda)R(\lambda)$によって計算できます。

色材の色をXYZ表色系で表す

色を定量的に表す方法に三色表色系があります。

三色表色系とは任意の色光を3種用意し、それらを混合して対象の色と等しい色を表示する方法です。このとき定めた3種の色光を原刺激、それらの混合量を刺激値と呼びます。また、光の各波長に対応する刺激値を等色係数、その関数を等色関数と呼びます。

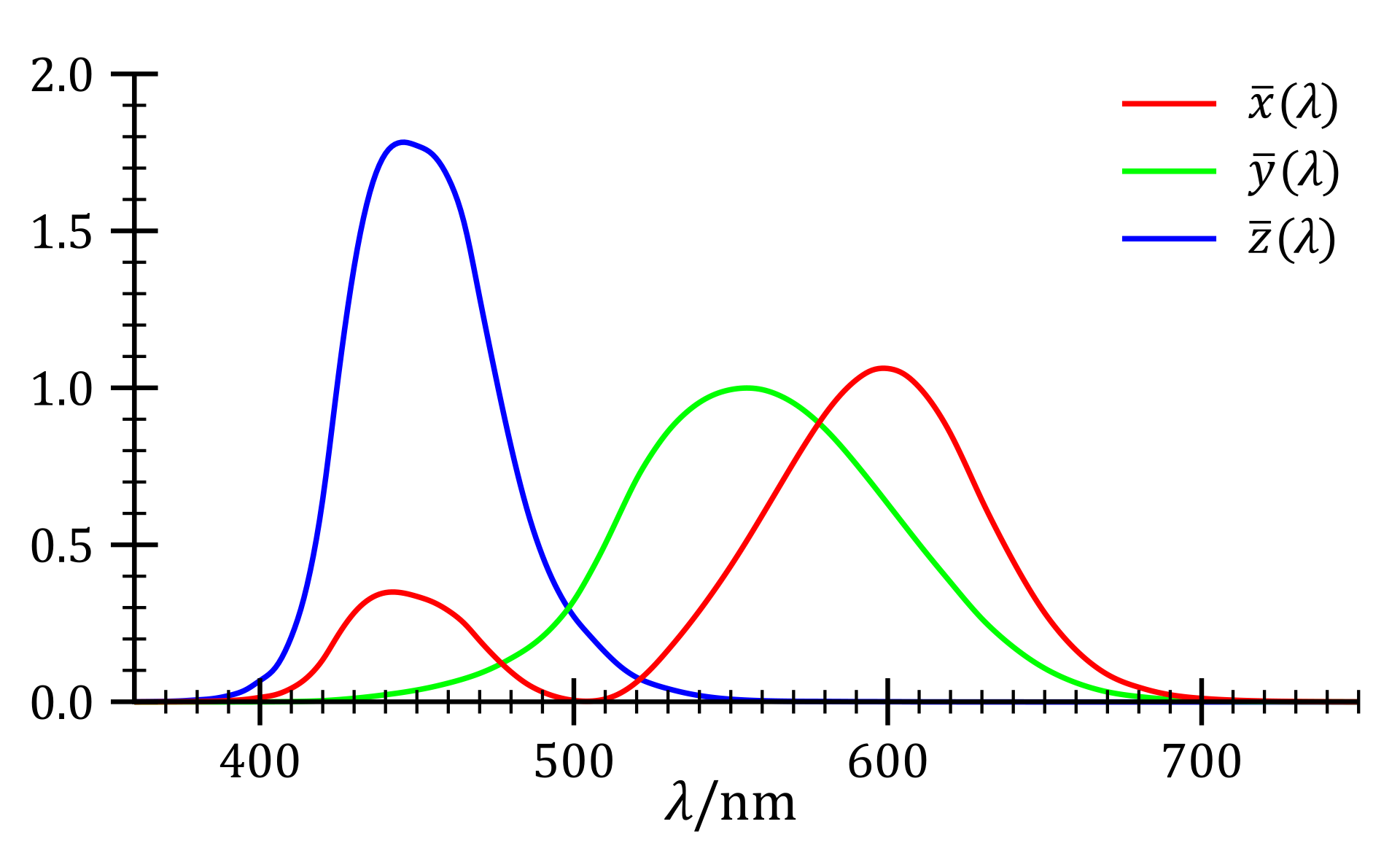
三色表色系の一つであるXYZ表色系（CIE 1931 XYZ）は、原刺激$[\mathrm{X}]$, $[\mathrm{Y}]$, $[\mathrm{Z}]$の等色関数$\bar{x}(\lambda)$, $\bar{y}(\lambda)$, $\bar{z}(\lambda)$を次のグラフのように定義しています。²

たとえば、$\lambda=470\mathrm{[nm]}$の光を表示するための等色係数はおおよそ$\bar{x}(\lambda)$=0.2, $\bar{y}(\lambda)=0.1$, $\bar{z}(\lambda)=1.5$です。

エネルギーの加法性から刺激値$X$, $Y$, $Z$は、物体の反射光の分光分布によって等色関数を重み付けし、波長について積分して求められます。このとき波長の範囲は可視波長域です。

\displaylines{
X=\frac{1}{Y_{D_{65}}}\int_{\lambda}\bar{x}(\lambda)D_{65}(\lambda)R(\lambda)d\lambda \\
Y=\frac{1}{Y_{D_{65}}}\int_{\lambda}\bar{y}(\lambda)D_{65}(\lambda)R(\lambda)d\lambda \\
Z=\frac{1}{Y_{D_{65}}}\int_{\lambda}\bar{z}(\lambda)D_{65}(\lambda)R(\lambda)d\lambda
}
\tag{1}

なお$Y_{D_{65}}=\int_{\lambda}\bar{y}(\lambda)D_{65}(\lambda)d\lambda$は刺激値を正規化するための係数です。

以上の方法により、色材をXYZ表色系で表すことができます。

XYZ表色系からsRGBへ変換する

続いて、XYZ表色系からsRGBへ変換します。sRGBはモニターなどのデバイスで色を扱うための標準的なRGB色空間であり、私たちが普段「RGB」と呼んでいるそれです。

sRGBの原刺激$[\mathrm{R}]$, $[\mathrm{G}]$, $[\mathrm{B}]$はXYZ表色系の原刺激$[\mathrm{X}]$, $[\mathrm{Y}]$, $[\mathrm{Z}]$を混合することで表現できます。したがって刺激値$X$, $Y$, $Z$から$R$, $G$, $B$への変換も可能です。

\begin{bmatrix}
R\\
G\\
B\\
\end{bmatrix}
=\begin{bmatrix}
+3.2406 & -1.5372 & -0.4986\\
-0.9689 & +1.8758 & +0.0415\\
+0.0557 & -0.2040 & +1.0570
\end{bmatrix}
\begin{bmatrix}
X\\
Y\\
Z\\
\end{bmatrix}
\tag{2}

Kubelka-Munk理論を応用して色材の混色を計算する

複数の色材を混合すると、性質の異なる粒子が互いの反射光を繰り返し散乱・吸収します。そのため、単純なRGBの加重平均では混色を正しく計算することができません。

Kubelka-Munk理論によると、色材の反射率から散乱係数および吸収係数を次式によって計算できます。

\frac
    {K(\lambda)}
    {S(\lambda)}
=\frac
    {{\bigl(
        1-R(\lambda)
    \bigr)}^2}
    {2R(\lambda)}
\tag{3}

$K(\lambda)$、$S(\lambda)$、$R(\lambda)$は波長$\lambda$の光に対する散乱係数、吸収係数、反射率です。式(1)を反射率$R(\lambda)$について解くと次式が得られます。

R(\lambda)
=1
+\frac
    {K(\lambda)}
    {S(\lambda)}
-\sqrt
    {
        \frac
            {{K(\lambda)}^2}
            {{S(\lambda)}^2}
        +2\frac
            {K(\lambda)}
            {S(\lambda)}
    }
\tag{4}

散乱係数$K(\lambda)$と吸収係数$S(\lambda)$はそれぞれ加法性が成立すると仮定します。すると、$N$個の色材を濃度$\boldsymbol{\mathrm{c}}$で混ぜたときの乱係数$K_{mix}(\boldsymbol{\mathrm{c}}, \lambda)$と吸収係数$S_{mix}(\boldsymbol{\mathrm{c}}, \lambda)$は次式によって計算できます。

\displaylines{
K_{mix}(\boldsymbol{\mathrm{c}}, \lambda)=
\sum_{i=1}^{N}c_iK_i(\lambda)\\
S_{mix}(\boldsymbol{\mathrm{c}}, \lambda)=
\sum_{i=1}^{N}c_iS_i(\lambda)
}
\tag{5}

ところで混色の反射率$R_{mix}(\boldsymbol{\mathrm{c}}, \lambda)$には、色材の鏡面反射と拡散反射の両方の情報が含まれています。鏡面反射とは媒体の境界での反射のことであり、色は入射光と変わりません。一方、拡散反射とは媒体の境界を透過した光の反射のことであり、媒体の色を反映します。Kubelka-Munk理論は拡散反射を前提としているので、鏡面反射に関する係数$k_1$と拡散反射に関する係数$k_2$を用いて反射率を補正します。

{{R}^{'}}_{mix}(\boldsymbol{\mathrm{c}}, \lambda)
=\frac
    {(1-k_1)(1-k_2)R_{mix}(\boldsymbol{\mathrm{c}}, \lambda)}
    {1-k_2R_{mix}(\boldsymbol{\mathrm{c}}, \lambda)}
\tag{6}

したがって色材の混色のRGBは、式(3), (5), (4), (6), (1), (2)を順に計算して求めることができます。

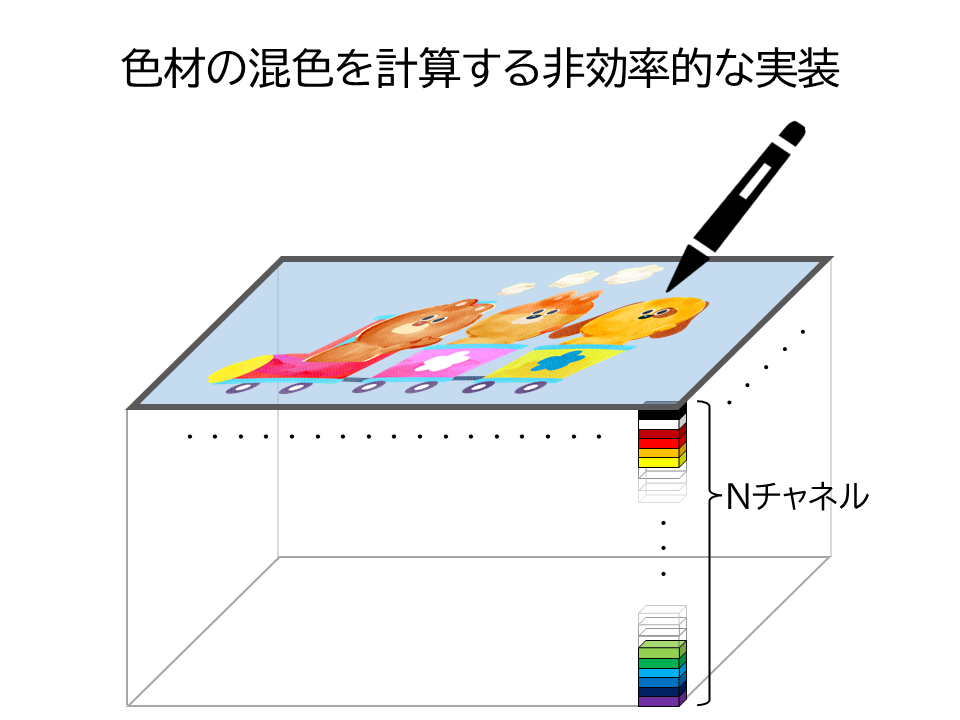
色材の混色を計算する非効率的な実装

しかし上記の計算方法をソフトウェアに実装しようすると、すぐさま困難に直面します。

はじめに開発者たちは何種類もの色材をパレットに並べてユーザーを満足させようと考えます。RGBチャネルを基にしたペインティングツールを使い慣れているユーザーは$256^{3}=16777216$通りの色材を求めるからです。しかしそれは$256^{3}$個という膨大な数の分光分布を測定しなけらばならないことを意味します。

$256^{3}$個には程遠いですが、どうにか$N$個の色材の分光分布を測定した開発者たちは、つぎに混色の計算を実装しました。ところが完成したソフトウェアはタブレットペンの動きにブラシがついてこれません。ソフトウェアは$W \times H$のキャンバスのピクセル一つ一つに対して$N$個の色材の濃度を追跡しており、ブラシが通過するたびに積分や行列計算をしなければなりません。そのためチャネル数や計算が負荷となり、動作が重くなってしまったのです。

MixBox

MixBoxはRGBチャネルのまま色材の混色を効率的に計算できます。手順は次の通りです。

1. RGBから潜在ベクトルへの変換

はじめにRGBを「原色材」（primary pigments）の濃度によって表現します。論文では以下の色を原色材に選びました。

原色材	イメージ
フタロ・ブルー	#110280
ハンザ・イエロー	#FCDB09
キナクリドン・マゼンタ	#8D0649
チタニウム・ホワイト	#FFFFFF

原色材の集合を$\mathcal{P^*}=\lbrace(K_{i}^*(\lambda), S_{i}^*(\lambda))\rbrace_{i=1}^4$とします。$\boldsymbol{\mathrm{RGB}}$から$\mathcal{P^*}$の濃度$\boldsymbol{\mathrm{c}}$への変換式は次のように書けます。

\boldsymbol{\mathrm{c}}=
\underset{
  \mathcal{P^*}
  }{
  unmix
  }(
  \boldsymbol{\mathrm{RGB}}
)
\tag{7}

数値解析によって$\boldsymbol{\mathrm{RGB}}$とのユークリッド距離が最小となるような$\boldsymbol{\mathrm{c}}$を求めることができます。

\underset{
  \mathcal{P^*}
  }{
  unmix
  }( 
  \boldsymbol{\mathrm{RGB}}
)=
\underset{
  \boldsymbol{\mathrm{c}}
}{\operatorname{arg\:min}}\:
||
\underset{
  \mathcal{P^*}
}{mix(\boldsymbol{\mathrm{c}})}-
\boldsymbol{\mathrm{RGB}}
||^2
\tag{8}

ただしRGB色空間には色材の混色によって表現できない領域があるため、それらの残差$\boldsymbol{\mathrm{r}}$も計算します。

\boldsymbol{\mathrm{r}}=
\boldsymbol{\mathrm{RGB}}-
\underset{
  \mathcal{P^*}
  }{
  mix
  }(
  \boldsymbol{\mathrm{c}}
)
\tag{9}

したがって$\boldsymbol{\mathrm{RGB}}$から潜在ベクトル$\boldsymbol{\mathrm{z}}=[c_1, c_2, c_3, c_4, r_R, r_G, r_B]^T$へのエンコーダ$\mathcal{F}$は次のように表せます。

\mathcal{F}(
  \boldsymbol{\mathrm{RGB}}
)=
\begin{bmatrix}
  \boldsymbol{\mathrm{c}} \\
  \boldsymbol{\mathrm{r}}
\end{bmatrix}=
\begin{bmatrix}
  {unmix(\boldsymbol{\mathrm{RGB}})} \\
  \boldsymbol{\mathrm{RGB}}-{mix(\boldsymbol{\mathrm{c}})}
\end{bmatrix}=
\boldsymbol{\mathrm{z}}
\tag{10}

2. 潜在ベクトルの加重平均

つづいて混色の重みに応じて潜在ベクトル$\boldsymbol{\mathrm{z}}$を加重平均します。

\boldsymbol{\mathrm{z}} =
\sum_{i=1}^{N}w_i\boldsymbol{\mathrm{z}}_i
\tag{11}

3. 潜在ベクトルからRGBへの逆変換

最後に加重平均した潜在ベクトル$\boldsymbol{\mathrm{z}}$をデコーダ$\mathcal{G}$によって$\boldsymbol{\mathrm{RGB}}$に逆変換します。

\mathcal{G}(
  \boldsymbol{\mathrm{z}}
)=
\mathcal{G}\Biggl(
\begin{bmatrix}
  \boldsymbol{\mathrm{c}} \\
  \boldsymbol{\mathrm{r}}
\end{bmatrix}
\Biggl)=
{mix(\boldsymbol{\mathrm{c}})}+
\boldsymbol{\mathrm{r}}=
\boldsymbol{\mathrm{RGB}}
\tag{12}

実装上の工夫

Surrogate Pigments

原色材の混色にもRGBによって表現できない領域が存在するので、潜在ベクトルとRGBの変換/逆変換を繰り返すたびに誤差が生じてしまいます。これを回避するために「代替色材」（surrogate pigments）$\mathcal{Q^*}$を計算します。つまり、混色がRGB空間で表現できる範囲に収まり、かつできるかぎり原色材と似た分光特性をもつ色材を代わりに用いるのです。式は次の通りです。

\mathcal{Q^*}=
\underset{
  \boldsymbol{\mathcal{Q}}
}{\operatorname{arg\:min}}\:
E_{push}(\mathcal{Q})+
\alpha E_{pull}(\mathcal{Q}, \mathcal{P^*})
\tag{13}

$E_{push}(\mathcal{Q})$は$\mathcal{Q}$の混色がRGB空間から「流出」する量を表します。

E_{push}(\mathcal{Q}) =
\int_{\partial \Omega}
max(
  0,
  \phi(
    \underset{
      \boldsymbol{\mathcal{Q}}
    }{
      \operatorname{mix}
    }
    (
        \mathrm{c}
    )
  )
)^2
ds
\tag{14}

$\partial \Omega$は$\mathcal{Q}$の混色の色域が成す閉曲面です。$\phi$はRGB空間の色域（立方体）が成す閉曲面から$\mathcal{Q}$の混色への法線ベクトルのノルムです。

一方、$E_{pull}(\mathcal{Q}, \mathcal{P^*})$は濃度$\mathrm{c}$における$\mathcal{P^*}$と$\mathcal{Q}$の混色の色差を表します。

E_{pull}(\mathcal{Q}, \mathcal{P^*}) =
\int_{\partial \Omega}
||
  \psi(
    \underset{
      \boldsymbol{\mathcal{Q}}
    }{
      \operatorname{mix}
    }
    (
        \mathrm{c}
    )
  )-
  \psi(
    \underset{
      \boldsymbol{\mathcal{P^*}}
    }{
      \operatorname{mix}
    }
    (
        \mathrm{c}
    )
  )
||^2
ds
\tag{15}

$\psi$はRGB色空間からOklab色空間³へ変換する関数です。Oklabは$(L,a,b)$座標のユークリッド距離がそのまま色差となります。

LUT

MixBoxは${unmix(\boldsymbol{\mathrm{RGB}})}$と${mix(\boldsymbol{\mathrm{c}})}$をあらかじめ計算し、ルックアップテーブル(LUT)を用意することで高速化を図っています。濃度$\boldsymbol{\mathrm{c}}$は$N-1=3$個の値がわかればよいので、テーブルのサイズは

8[\mathrm{bit}] \times 3 \times 256^3 \times 2=
805306368[\mathrm{bit}]\approx
96[\mathrm{MB}]

となります。さらにこれを2つの$4096 \times 4096$のPNG画像に変換し、7MBにまで圧縮できたと論文では述べられています。

しかし実装上はRGBの量子化ビット数を$4\mathrm{[bit]}$とする$512 \times 512$のLUTを3次元線形補間して用いているようです。以下はUnity Shader用のLUTです。⁴またPythonに関しては、LUTをBase64でエンコードしたテキストを読み込んでいました。

Pythonライブラリ

pip install pymixboxでインストールできます。以下は主要な関数です。

関数	機能	引数	戻値
lerp_float	2色のFloat RGB(A)を混色する	color1: ArrayLike # Float RGB(A) color2: ArrayLike # Float RGB(A) t: float # color1 : color2 = 1 - t : t	タプル型のFloat RGB(A)
lerp	2色のRGB(A)を混色する	color1: ArrayLike # RGB(A) color2: ArrayLike # RGB(A) t: float # color1 : color2 = 1 - t : t	タプル型のRGB(A)
float_rgb_to_latent	Float RGBを潜在ベクトルに変換する	rgb: ArrayLike # Float RGB	タプル型の潜在ベクトル
rgb_to_latent	RGBを潜在ベクトルに変換する	rgb: ArrayLike # RGB	タプル型の潜在ベクトル
latent_to_float_rgb	潜在ベクトルをFloat RGBに逆変換する	latent: ArrayLike # 潜在ベクトル	タプル型のFloat RGB
latent_to_rgb	潜在ベクトルをRGBに逆変換する	latent: ArrayLike # 潜在ベクトル	タプル型のRGB

1. Kevin Houser (Loucetios) - The raw spectral data are from CIE Publication 15.2 Colorimetry. Values for (x, y), CCT, and CRI were computed using software developed by me as a teaching tool for AE 9200 Color Theory, which I teach at the University of Nebraska, パブリック・ドメイン, https://commons.wikimedia.org/w/index.php?curid=868392による ↩

2. By User:Acdx - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=6233111 ↩

3. Björn Ottosson. "A perceptual color space for image processing". https://bottosson.github.io/posts/oklab/. ↩

4. https://github.com/scrtwpns/mixbox/blob/master/unity/Textures/MixboxLUT.png ↩