　ちょっと探せば力学系の情報は無限に出てきますが、自分で整理したいと思ったので残しておきます。以下はちゅらデータでの社内研修を一部圧縮して一部丁寧にしたような内容です。

力学系とは

連続と離散

　以下ふたつの条件を満たす可微分関数 $\varphi: T\times S\rightarrow S$ を力学系といい、特に時刻 $T$ が $\mathbb{R}$ の場合は連続力学系、$\mathbb{Z}$ の場合は離散力学系と呼びます。

$\varphi\left(0, \cdot\right)$ は恒等関数
任意の時刻 $t_1, t_2 $ に対し $\varphi\left(t_1,\cdot\right)\circ \varphi\left(t_2, \cdot\right) = \varphi\left(t_1+t_2, \cdot\right)$

　つまりは動く点の時刻 $0$ での初期状態 $x \in S$ から正または負の時間経過したときの状態を返す関数というわけです。ふたつめの条件は「どの時刻から観察を始めても遷移は同じ」ということを表現しています。連続力学系は、関数 $x\left(t\right) = \varphi\left(t,x\right)$ を解とする微分方程式
$$\frac{dx}{d t} = f\left(t, x\right)$$
を与えます。$f$ が $t$ に依存するときこの力学系を非自励系、そうでないとき自励系と呼びます。

　離散の場合は漸化式が与えられます。離散力学系は時刻のステップ幅が $1$ なので、
$$\varphi\left(n, x\right) = \varphi\left(1, \varphi\left(n-1, x\right)\right) = \cdots = \varphi\left(1, \varphi\left(1, \cdots, \varphi\left(1, x\right)\cdots\right)\right)$$
というふうに関数 $\varphi\left(x\right) = \varphi\left(1,x\right)$ の反復 $\varphi^n\left(x\right)$ を考えれば十分です。これに対し漸化式
$$\left(\varphi^n\left(x_0\right) =\right) x_n = \varphi\left(x_{n-1}\right)$$
が考えられます。漸化式のことを差分方程式と呼ぶこともありますし、$\Delta x_n = x_n - x_{n-1}$ として
$$\Delta x_n = f\left(n, x_{n-1}\right)$$
のように差分の形に変形できる場合のみ差分方程式と呼ぶこともあります。

連続力学系の例

　簡単な例を考えてみましょう。質量 $m$ の球が長さ $l$ の棒で支えられているとします。また、摩擦力 $-kl \cdot d\theta /dt \ \left(k\geq 0\right)$ がかかっているとします。棒の鉛直線からの反時計回りの角度を $\theta$ とすると、角速度は $\omega = d\theta / dt$ で表されます。

　球の動きは以下の微分方程式で表現されます。
$$
\begin{align}
\frac{d\theta}{dt} &= \omega \\
\frac{d\omega}{dt} &= -\frac{1}{l}\sin\theta - \frac{k}{m}\omega
\end{align}
$$

離散力学系の例

　離散力学系の例としてロジスティック写像 $f\left(x\right) = ax\left(1-x\right)$ によるものがよく知られています。$a\in \left[0,4\right]$ として、$\left[0, 1\right]$ 上の列が漸化式
$$x_n = a x_{n-1}\left(1 - x_{n-1}\right)$$
で定義されているとします。これは生物の個体数の世代ごとの変化を記述するモデルによく利用されます。また、擬似乱数の生成にも利用されます。

　この離散力学系は繁殖率パラメータ $a$ によって収束・周期振動・カオスのうちどの振る舞いをするかが分かれます。

# ロジステック関数を定義する
def logistic(a, x_0=0.5):
    # 初期値を設定
    x_n = [x_0]
    x_append = x_n.append
    # 繰り返し適用
    for i in range(400):
        x_append(a * x_n[-1] * (1 - x_n[-1]))
    # ある程度定常的になってからの動きを取る
    x_n = x_n[-100:]

    return x_n

# 各 a について縦に点を 100 個描画
for a in np.linspace(0, 4, 500):
    plt.plot([a]*100, logistic(a), 'b.', markersize=1.7)

plt.xlabel('繁殖率 a', size=16)
plt.ylabel('個体数 x', size=16)
plt.show()

平衡点とその安定性

平衡点

　力学系の不動点を平衡点と呼びます。すなわち、任意の時刻 $t$ に対して $\varphi\left(t,\bar{x}\right)=\bar{x}$ となるような $\bar{x} \in S$ のことです。
　連続自励系 $x' = f\left(x\right)$ について考えてみましょう。以下、プライム記号 $'$ で時刻 $t$ についての微分を表します。点 $\bar{x}$ 付近で $S\subseteq \mathbb{R}^d$ 上の関数 $f$ をテイラー展開すると
$$f\left(\bar{x}+\varepsilon \right) \approx f\left(\bar{x}\right) + \sum_{i=1}^{d} \partial_i \ f\left(\bar{x}\right)\varepsilon_i$$
と近似されます。よって、$x\left(t\right)$ の点 $\bar{x}$ からのズレを $u\left(t\right) = x\left(t\right) - \bar{x}$ とおくと、
$$
\begin{pmatrix}
u_1' \\
\vdots\\
u_d'
\end{pmatrix} =
\begin{pmatrix}
f_1\left(\bar{x} + u \right) \\
\vdots\\
f_d\left(\bar{x} + u \right)
\end{pmatrix} \approx
\begin{pmatrix}
f_1\left(\bar{x}\right) \\
\vdots\\
f_d\left(\bar{x}\right)
\end{pmatrix} +
\begin{pmatrix}
\partial_1\ f_1\left(\bar{x}\right) & \cdots & \partial_d\ f_1\left(\bar{x}\right)\\
\vdots & \ddots & \vdots \\
\partial_1\ f_n\left(\bar{x}\right)& \cdots & \partial_d\ f_d\left(\bar{x}\right)
\end{pmatrix}
\begin{pmatrix}
u_1 \\
\vdots\\
u_d
\end{pmatrix} = f\left(\bar{x}\right)+ df_{\bar{x}} \ u
$$
というふうに微分が点 $\bar{x}$ におけるヤコビ行列 $df_{\bar{x}}$ を用いて近似できます。定数ベクトル $\bar{x}$ は微分によって消えて $u'=x'$ となり、$\bar{x}$ が平衡点の場合は $f\left(\bar{x}\right) = 0$ となるので
$$x' \approx df_{\bar{x}}\left(x - \bar{x}\right)$$
という近似が得られます。座標変換すれば以後得られる結果は同じであるため、一般性を失わず $\bar{x}=0$ とできます。すると、微分方程式 $x' = f\left(x\right)$ が平衡点 $0$ のまわりでヤコビ行列 $A = df_0$ によって $x' \approx Ax$ と線形化されたことになります。
　以上より、連続力学系の平衡点の性質は線形部分 $A$ について調べればわかりそうだと考えられます。

連続力学系の平衡点の安定性

　平衡点の安定性にはいくつかの定義があります。最もよく使われるものはリャプノフ安定性と呼ばれる定義でしょう。平衡点 $\bar{x}$ の任意の近傍 $N\left(\bar{x}\right)$ に対し適切に部分近傍 $\tilde{N}\left(\bar{x}\right)\subseteq N\left(\bar{x}\right)$ を取れば $\tilde{N}\left(\bar{x}\right)$ から出る任意の軌道が $N\left(\bar{x}\right)$ 内に留まるとき、$\bar{x}$ は安定であるといい、そのような部分近傍が取れないとき不安定であるといいます。安全な平衡点 $\bar{x}$ が $\tilde{N}\left(\bar{x}\right)$ から出る任意の軌道の $t\rightarrow\infty$ での極限になっているときに漸近安定であるといいます。

　平衡点がこのうちどれに当たるかを知るためにはどうすればいいでしょうか。先ほど見たように、平衡点のまわりは局所的に $x'\approx Ax$ と線形化できました。行列 $A$ の性質をよく表す量として、固有値がありました。固有値は特性方程式 $\det \left(A - \lambda I\right) = 0$ の解 $\lambda$ として計算できます。
　線形部分の固有値の実部が負であれば平衡点は周辺の点を近寄せ、正であれば遠ざけます。固有値に純虚数があるような平衡点を楕円型、すべての固有値の実部が非零であるような平衡点を双曲型といいます。双曲型平衡点のうちすべての固有値の実部が正であるものは湧点、すべての固有値の実部が負であるものは沈点、正負が入り混じっているものは鞍点と呼ばれます。湧点と鞍点は不安定、沈点は漸近安定なので、漸近安定ではないが安定という平衡点は楕円型に限られます。実は、実部が正のものがあればひとつでもあれば不安定になるという不安定性定理が成り立ちます。

　実際に、連続力学系の平衡点の安定性を調べてみましょう。感染症の広がりは SIR モデルを用いてモデリングする場合が多いということは最近ならよく聞くのではないでしょうか。時刻 $t$ での未感染人口、感染人口、治癒人口をそれぞれ

$$
\begin{align}
S' &= -\beta SI \\
I' &= \beta SI - \gamma I \\
R' &= \gamma I
\end{align}
$$

で定義します。パラメータ $\beta$ と $\gamma$ はそれぞれ感染率と治癒率を表し、治癒率は $I$ から $R$ への移行期間 $D$ の逆数 $D^{-1}$ となっています。$S'+R'+I'={\left(S+R+I\right)}' = 0$ より、総人口 $N=S+R+I$ は一定なので、$S,R,I$ のうちふたつを考えれば全体の動きはわかります。平衡点では微分が $0$ になるので、

$$
\begin{pmatrix}
S' \\
I' \\
R'
\end{pmatrix} =
\begin{pmatrix}
-\beta SI \\
\beta SI - \gamma I \\
\gamma I
\end{pmatrix} =
\begin{pmatrix}
0 \\
0 \\
0
\end{pmatrix}
$$

となる点 ${\left(S, 0, R\right)}^\top\ \left(S, R>0\right)$ たちが平衡点となります。定常状態になるためには感染者数が $0$ になる必要があるというのは直感に沿う結果です。この平衡点のまわりの線形部分（ヤコビ行列）は

$$
\begin{pmatrix}
0 & -\beta S & 0\\
0 & \beta S - \gamma & 0\\
0 & \gamma & 0
\end{pmatrix}
$$

であり、固有値は $0, \beta S - \gamma$ です。不安定性定理より、未感染人口が $\mathrm{Re}\left(\beta S - \gamma\right) > 0$ すなわち $S > \gamma\cdot \beta^{-1}$ を満たすとき不安定であることがわかります。

# SIRモデルを定義する  ※ R0 は基本再生産数: R0 = beta * N / gamma
def SIR(N, gamma, R0, I_0=1, n_step=200):
    beta = R0 * gamma / N
    # 最初に1人が感染
    S_0, I_0, R_0, Rt_0 = (1, I_0/N, 0, R0)
    S_n, I_n, R_n, R_t = [S_0], [I_0], [R_0], [Rt_0]
    S_append, I_append, R_append, Rt_append =\
        S_n.append, I_n.append, R_n.append, R_t.append
    for n in range(n_step):
        S_append(S_n[-1] - beta * N * S_n[-1] * I_n[-1])
        I_append(I_n[-1] + beta * N * S_n[-1] * I_n[-1] - gamma * I_n[-1])
        R_append(R_n[-1] + gamma * I_n[-1])
        Rt_append(beta * N * S_n[-1] / gamma)

    return S_n, I_n, R_n, R_t

# SIRモデルでシミュレート
N = 1.26 * 1e8  # 日本の人口
R0 = 2  # 基本再生産数
gamma = 0.2  # 治癒率

S, I, R, Rt = SIR(N=N, gamma=gamma, R0=R0)

fig, (ax1, ax2) = plt.subplots(2,1, gridspec_kw={'height_ratios':[3, 1]})
ax1.plot(S, color='b', label='未感染人口', linewidth=4)
ax1.plot(I, color='r', label='感染人口', linewidth=4)
ax1.plot(R, color='g', label='治癒人口', linewidth=4)
ax2.plot(Rt, color='k', label='実効再生産数', linewidth=4)
ax1.legend()
ax2.legend()
plt.show()

　あるいは、リャプノフ関数を構成して安定性を調べる方法もあります。平衡点 $\bar{x}$ の近傍で微分可能な連続関数 $V: N\left(\bar{x}\right) \rightarrow \mathbb{R}$ が以下の条件を満たすとき、リャプノフ関数といいます（ $\langle\cdot\mid\cdot\rangle$ は内積です）。

　1. $V\left(\bar{x}\right) = 0$
　2. $x \neq \bar{x}$ に対し $V\left(x\right) > 0$
　3. $N\left(\bar{x}\right)\setminus\left\{\bar{x}\right\}$ 上で $\langle \nabla V\mid x'\rangle \leq 0$

　また、条件 3 の $\leq$ を $<$ に変えた場合を狭義リャプノフ関数といいます。平衡点に対してリャプノフ関数が存在するとき安定、狭義リャプノフ関数が存在するとき漸近安定ということがわかります。
　例えば、連続力学系

$$
\begin{pmatrix}
x_1' \\
x_2' \\
x_3'
\end{pmatrix} =
\begin{pmatrix}
2x_2\left(x_3 - 2\right) \\
- x_1\left(x_3 - 1\right) \\
x_1 x_2
\end{pmatrix}
$$

の平衡点 $0 = {\left(0,0,0\right)}^\top$ の安定性が知りたいとします。関数 $V$ を
$$V\left(x\right) = x_1^2 + 4x_2^2 + 2x_3^2$$
で定義すると、これはリャプノフ関数になっているので $0$ は安定な平衡点であることがわかります。実際、$V\left(0\right)=0$ かつ $V\left(x\right) > 0 \ \left(x\neq 0\right)$ であり、

$$
\begin{align}
\langle\nabla V\mid x'\rangle &=2x_1\times 2x_2\left(x_3-2\right)+8x_2 \times\left(-x_1\left(x_3 - 1\right)\right)+4x_3\times x_1 x_2 \\
&=4x_1x_2x_3 - 8x_1 x_2 - 8x_1 x_2 x_3 + 8x_1 x_2 + 4 x_1 x_2 x_3 \\
&= 0
\end{align}
$$

とリャプノフ関数の条件を満たしていることが確認できます。

離散力学系の平衡点の安定性

　離散力学系に対しても同様に安定性を考えます。ただし、不連続なので平衡点のまわりで線形近似するというやり方はできません。そのため、ステップ数を大きくしていったらどうなるかということを見ていきます。離散力学系が与える漸化式
$$x_n = \sum_{i=0}^{k} c_i x_{n-1}^i$$
に対し、特性方程式
$$\mu = \sum_{i=0}^{k}c_i \mu^i$$
を考えます。この解として平衡点が得られます。また、その平衡点は関数
$$F\left(\mu\right) = \sum_{i=0}^{k} c_i \mu^i$$
の微分の絶対値が $1$ であれば安定、$1$ 未満であれば漸近安定、$1$ を超えれば不安定であることがわかります。

　例えば、漸化式
$$x_n = \frac{2}{7}x_{n-1}^2 + \frac{3}{7}$$
を与える離散力学系の平衡点は、特性方程式
$$\mu = \frac{2}{7}\mu^2 + \frac{3}{7}$$
の解である $1/2$ および $3$ です。関数
$$F\left(\mu\right) = \frac{2}{7}\mu^2 + \frac{3}{7}$$
の微分 $4\mu / 7$ の絶対値をそれぞれの平衡点について計算すると、平衡点 $1/2$ に対しては $2/7 < 1$、$3$ に対しては $12/7 > 1$ となるため、それぞれ漸近安定、不安定であることがわかります。

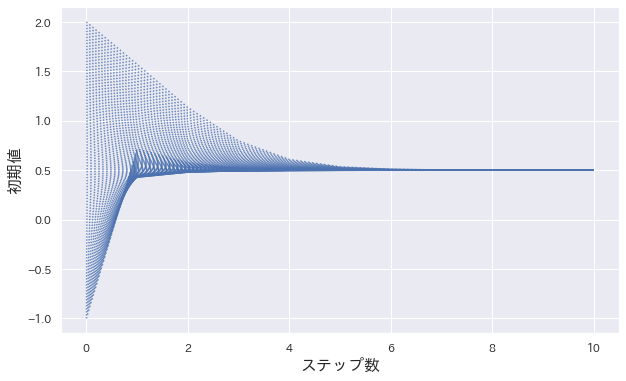
　$1/2$ より小さな初期値からスタートすると徐々に $1/2$ へ収束していき、$1/2$ から $3$ までの間の初期値からもまた $1/2$ へ近づいていくことが見て取れます。また、それより大きな初期値からスタートするとオーバーフローエラーが返ってきます。

# 離散力学系を漸化式で定義する
next_step = lambda now_step: (2/7)*(now_step**2) + (3/7)

def dynamics(x_0, times=75):
    x_n = [x_0]
    x_append = x_n.append
    for i in range(times):
        x_append(next_step(x_n[-1]))

    return x_n

# 平衡点 1/2 と 3 のまわりで何が起こるかを確認する
start_points = np.linspace(-1, 2, 100)

for n in start_points:
    y = dynamics(n)
    x = range(len(y))
    plt.plot(x, y, linestyle=':', color='b', alpha=0.8)

plt.xlabel('ステップ数', size=16)
plt.ylabel('初期値', size=16)
plt.show()