ニューラルネットワークとは
物質中の原子は相互に影響を及ぼし合っています、この相互作用をすべて足し合わせて求まる系のエネルギーをポテンシャルエネルギーと言います。ポテンシャルエネルギーと原子の座標の関係がわかっていれば、ポテンシャルエネルギーを原子の座標で微分することで、それぞれの原子にかかる力を求めることができ、構造最適化計算や分子動力学計算をすることができます。原子間の相互作用を高精度に知るには、第一原理計算という、量子力学に基づいた計算をする必要がありますが、この第一原理計算は計算コストが大きいです。そこで、原子の座標の関数であるポテンシャルエネルギーをニューラルネットワークによって近似することで、計算コストの大きい第一原理計算をバイパスし、分子動力学計算などができます。これがニューラルネットワークポテンシャルです。
本記事では、ニューラルネットワークポテンシャルの一つである、DeepPot-SEを実際に実装します。
今回実装するニューラルネットワークポテンシャル
本記事では、"DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics"(Computer Physics Communications
Volume 228, July 2018, Pages 178-184)を実装します。アーキテクチャなどは詳しく説明しないので、論文を読んで下さい。論文と違う実装をしたところが2箇所あります。1つ目は、論文ではAtomTypeEmbeddingを使用していませんが、本記事では使用したところです。2つ目は、スイッチ関数です。これらは後で触れます。
前提
$E$ : 全エネルギ
$E_i$ : 原子$i$の持つエネルギー
$N$ : 全原子数
$N_i$ : 原子$i$のカットオフ半径内の原子数
$i$ : $i$番目の原子、$i = 0, 1, 2, ...., N-1$
$j$ : $i$番目の原子の隣接原子$j$、$j = 0, 1, 2, ...., N_i-1$
$R$ : 原子の座標の行列、shapeは[$N$, 3]
$R_i$ : 原子$i$から見た隣接原子の行列、shapeは[$N_i$, 3]
$\hat{R_i}$ : 変換後の原子$i$から見た隣接原子の行列、shapeは[$N_i$, 4]
$m_1$, $m_2$ : 定数、ただし$m_1 > m_2$
$g_{i1}$ : $i$原子の周りの環境用のフィルター行列、shapeは[$N_i$, $m_1$]
$g_{i2}$ : $i$原子の周りの環境用のフィルター行列、shapeは[$N_i$, $m_2$]
$D_{i}$ : 原子$i$の周りの環境を表す特徴量行列、shapeは[$m_1$, $m_2$]
$T_i$ : 原子$i$のタイプ
$\text{AtomTypeEmbedNet()}$ : 原子のタイプ埋め込み用ニューラルネットワーク
$\text{EmbedNet()}$ : 埋め込み用ニューラルネットワーク
$\text{FittingNet()}$ : フィッティング用ニューラルネットワーク
Atom type embedding について
Embeddingというのは、人間が識別できるものから、そのモノを的確に表すような特徴量ベクトルに変換することです。今回は、Atom type embeddingなので、原子のタイプ(原子の種類)から、その原子のタイプを表す特徴量ベクトルに変換します。
まず、原子$i$のタイプ$T_i$をワンホットベクトルにします。ワンホットベクトルとは、一つだけ1になっていて、ほかの部分はすべて0になっているようなベクトルです。
例として、C H O N Si の5元素ある場合を考えます。原子のタイプはそれぞれCは1, Hは2, Oは3, Nは4, Siは5です。タイプが0の原子はないものとします。
この場合、
C原子のワンホットベクトルは、[0, 1, 0, 0, 0, 0]
H原子のワンホットベクトルは、[0, 0, 1, 0, 0, 0]
O原子のワンホットベクトルは、[0 ,0 , 0, 1, 0, 0]
N原子のワンホットベクトルは、[0, 0, 0, 0, 1, 0]
Si原子のワンホットベクトルは、[0, 0, 0, 0, 0, 1]
のようになります。
次に、これらの原子のタイプのワンホットベクトルを、AtomTypeEmbedNetというニューラルネットワークによって、特定の長さの特徴量ベクトルに変換します。
例えば、O原子の特徴量ベクトルは
$$\text{AtomTypeEmbedNet}([0, 0, 1, 0, 0])=[0.235, 0.131, 0.263, 4.242, ..., 1.633]$$
などのような、O原子を的確に表すような特徴量ベクトルに変換されます。
Atom type embeddingを用いる理由
もともとの論文では、原子$i$の持つポテンシャルエネルギー$E_i$を予測するのに、(原子のタイプの種類数)^2個のEmbeddingNetと(原子のタイプの種類数)個のFittingNetを用意しています。これは、原子$i$のタイプと原子$j$のタイプのペア用のEmbeddingNetに原子$i$と原子$j$の位置関係を入れることによって、フィルター行列$g_i$を作成します。また、原子$i$の周りの特徴量行列$D_i$を原子$i$のタイプ用のFittingNetに入れることで原子$i$のポテンシャルエネルギー$E_i$を予測します。この方法では、高速に動作させるプログラムを作ることが難しいです。
Atom type embeddingを用いると、1個のAtomTypeEmbeddingNetと1個のEmbeddingNetと1個のFittingNetですみます。これは、原子$i$のタイプの特徴量ベクトルと原子$j$のタイプの特徴量ベクトルと原子$i$と原子$j$の位置関係をEmbeddingNetに入れることで、フィルター行列$g_i$を作成します。また、原子$i$の周りの特徴量行列$D_i$と原子$i$のタイプの特徴量ベクトルをFittingNetに入れることで原子$i$のポテンシャルエネルギー$E_i$を予測します。このように、Atom type embeddingを用いることで、より効率的に計算できます。
実装
先に実装したコードを貼ります。
from pathlib import Path
import torch
import torch.nn as nn
import torch.nn.functional as F
from ase.neighborlist import neighbor_list as make_neighbor_list
import numpy as np
from ase import Atoms
from tqdm import trange, tqdm
from pprint import pprint
torch.set_default_tensor_type('torch.cuda.FloatTensor')
def smooth_cut_s_function(
r_ij_norm:torch.tensor,
r_cutoff:float,
)->torch.tensor:
"""DeepPot-SE function s(r_ij) of tensor version
As r_ij becomes larger than r_cutoff_smth, the output of the function begins to decrease,
and as more r_ij becomes larger, the output of the function smoothly becomes zero.
Parameters
----------
r_ij_norm : torch.tensor
shape : (Coordination Num of atom i,)
r_cutoff : float
cutoff
Returns
-------
s_vec : torch.tensor
shape : (Coordination Num of atom i,)
"""
r_cutoff_smth = 0.1
s_vec = torch.zeros_like(r_ij_norm)
flag = (r_ij_norm <= r_cutoff)
u = (r_ij_norm[flag] - r_cutoff_smth) / (r_cutoff - r_cutoff_smth)
s_vec[flag] = (u*u*u*(-6*u*u + 15*u - 10) + 1) / (r_ij_norm[flag])
return s_vec
class ThreeLayerPerceptron(nn.Module):
def __init__(self, input_size, hidden_size, output_size, activation_function):
super(ThreeLayerPerceptron, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.fc2 = nn.Linear(hidden_size, hidden_size)
self.fc3 = nn.Linear(hidden_size, output_size)
self.activation_function = activation_function
def forward(self, x):
x = self.fc1(x)
x = self.activation_function(x)
x = self.fc2(x)
x = self.activation_function(x)
x = self.fc3(x)
return x
class DeepPotSEModel(nn.Module):
"""atom type embedding version of DeepPotSE
"""
def __init__(self,
max_atom_type:int,
atom_type_embed_nchanl:int,
m1:int,
m2:int,
fitting_hidden_size:int,
r_cutoff:float,
activation_function,
sel:int,
):
"""
Parameters
----------
max_atom_type : int
Maximum type of atoms
Example:
For atoms of C H O N Si,
each atom has atom type 1, 2, 3, 4, 5,
so max_atom_type is 5.
atom_type_embed_nchanl : int
Number of features after conversion
when converting the atom type to a
feature vector representing the atom type.
m1 : int
Transform S(r) into a vector with m1 features.
See the DeepPotSE paper.
m2 : int
Transform S(r) into a vector with m1 features.
Take the first half of the m2 features
See the DeepPotSE paper.
fitting_hidden_size : int
Number of nodes in the hidden layer of the last fitting net
r_cutoff : float
Cutoff radius
activation_function : function
activation function
sel : int
The maximum number of atoms within the cutoff radius
of an atom when focusing on a particular atom.
Set to a sufficiently large value.
If it is set too large, it may slow down the calculation.
"""
super(DeepPotSEModel, self).__init__()
self.r_cutoff = r_cutoff
self.max_atom_type = max_atom_type
self.m1 = m1
self.m2 = m2
self.activation_function = activation_function
self.sel = sel
self.atom_type_embed_nchanl = atom_type_embed_nchanl
self.atom_type_embed_net = ThreeLayerPerceptron(
input_size=max_atom_type+1, # 1-indexed
hidden_size=atom_type_embed_nchanl,
output_size=atom_type_embed_nchanl,
activation_function=activation_function
)
self.embed_net = ThreeLayerPerceptron(
input_size=1 + 2*atom_type_embed_nchanl,
hidden_size=m1,
output_size=m1,
activation_function=activation_function
)
self.fitting_net = ThreeLayerPerceptron(
input_size=m1*m2 + atom_type_embed_nchanl,
hidden_size=fitting_hidden_size,
output_size=1,
activation_function=activation_function
)
def forward(
self,
coords:torch.tensor,
atom_types:torch.tensor,
atom_i_types:torch.tensor,
atom_j_types:torch.tensor,
atom_i_idxs:torch.tensor,
atom_j_idxs:torch.tensor,
shift:torch.tensor,
):
"""predict potential energy.
Parameters
coords : torch.tensor, shape : [Natoms, 3]
The coordinates of each atom
atom_types : torch.tensor, shape : [Natoms]
Types of each atom
atom_i_types : torch.tensor, shape : [Natoms*sel]
If 0 <= atom_i_idx < Natoms,
then all atom_i_types[atom_i_idx:(atom_i_idx + 1)*sel] are
filled with atom_types[atom_i_idx].
atom_j_types : torch.tensor, shape : [Natoms*sel]
If 0 <= atom_i_idx < Natoms and 0 <= j < sel,
then the value of atom_j_types[atom_i_idx*sel + j] is
the type of the j-th neighbor atom of atom i
atom_i_idxs : torch.tensor, shape : [Natoms*sel]
If 0 <= atom_i_idx < Natoms,
then all atom_i_idxs[atom_i_idx:(atom_i_idx + 1)*sel] are
filled with atom_i_idx.
atom_j_idxs : torch.tensor, shape : [Natoms*sel]
If 0 <= atom_i_idx < Natoms and 0 <= j < sel,
then the value of atom_j_idxs[atom_i_idx*sel + j] is
the atom_idx of the j-th neighbor atom of atom i
shift : torch.tensor, shape : [Natoms*sel, 3]
How much the atom j is shifted by the periodic boundary condition
"""
coords.requires_grad_(True)
relative_coords = self.coords_to_relative_coords(
coords=coords,
atom_i_idxs=atom_i_idxs,
atom_j_idxs=atom_j_idxs,
shift=shift,
)
generalized_coords = self.relative_coods_to_generalized_coords(
relative_coords=relative_coords,
r_cutoff=self.r_cutoff
)
atom_type_one_hot = torch.eye(self.max_atom_type + 1)
atom_type_embedded_matrix = self.atom_type_embed_net(atom_type_one_hot)
total_potential_energy = torch.tensor(0.0)
s_rij = generalized_coords[:,0].reshape(-1, 1)
atom_i_embedded_matrix = atom_type_embedded_matrix[atom_i_types]
atom_j_embedded_matrix = atom_type_embedded_matrix[atom_j_types]
g_i1s_before_embed = torch.concat((
s_rij,
atom_i_embedded_matrix,
atom_j_embedded_matrix,
), dim=1)
g_i1s = self.embed_net(g_i1s_before_embed).reshape(coords.shape[0], self.sel, self.m1)
generalized_coords = generalized_coords.reshape(coords.shape[0], self.sel, 4)
# g_i1^T @ generalized_coords
left = torch.bmm(
torch.transpose(g_i1s, 1, 2),
generalized_coords
)
# generalized_coords^T @ g_i1[:, :m2]
right = torch.bmm(
torch.transpose(generalized_coords, 1, 2),
g_i1s[:, :, :self.m2]
)
D_i_s_reshaped = torch.bmm(left, right).reshape(coords.shape[0], self.m1 * self.m2)
feature_vectors = torch.concat((
D_i_s_reshaped,
atom_type_embedded_matrix[atom_types]
), dim=1)
total_potential_energy = torch.sum(
self.fitting_net(feature_vectors)
)
return total_potential_energy
def coords_to_relative_coords(
self,
coords:torch.tensor,
atom_i_idxs:torch.tensor,
atom_j_idxs:torch.tensor,
shift:torch.tensor,
):
coords_concat = torch.concat((
coords,
torch.full((1, 3), 1e5)
), dim=0)
relative_coords = coords_concat[atom_j_idxs] - coords_concat[atom_i_idxs] + shift
return relative_coords
ThreeLayerPerceptronについて
ただの三層のニューラルネットワークです。
DeepPotSEModelの__init__について
max_atom_typeはintで、原子のタイプを1インデックスで始めたときの最大の原子のタイプです。C, H, O, N, Siの5元素あった場合は、それぞれの原子のタイプは1, 2, 3, 4, 5となるので、max_atom_typeは5です。
atom_type_embed_nchanlはintで、原子のタイプのワンホットベクトルをAtom Type Embeddingによって原子の特徴量ベクトルに変換するのですが、変換後の特徴量数です。
m1, m2は論文と同じです。
fitting_hidden_sizeはintで、FittingNetの隠れ層のノードの数です。
r_cutoffはカットオフ半径、activation_functionは活性化関数、selはカットオフ半径内に入りうる原子の数の最大値です。
self.atom_type_embed_net = ThreeLayerPerceptron(
input_size=max_atom_type+1, # 1-indexed
hidden_size=atom_type_embed_nchanl,
output_size=atom_type_embed_nchanl,
activation_function=activation_function
)
ここでは、Atom Type Embedding用のニューラルネットワークを定義しています。
input_sizeはmax_atom_type + 1です。タイプが0の原子は今回存在せず、データがないときはこれで埋めます。
self.embed_net = ThreeLayerPerceptron(
input_size=1 + 2*atom_type_embed_nchanl,
hidden_size=m1,
output_size=m1,
activation_function=activation_function
)
ここでは、フィルター行列を作成するためのニューラルネットワークを定義しています。input_sizeは1 + 2*atom_type_embed_nchanlです。1というのは論文で言う$s(r_{ij})$です。これに追加して、原子$i$のタイプの情報と原子$j$のタイプの情報を一緒に入れたいので、$s(r_{ij})$と原子$i$のタイプのEmbedding後の特徴量ベクトルと原子$j$のタイプのEmbedding後の特徴量ベクトルを入れます。
self.fitting_net = ThreeLayerPerceptron(
input_size=m1*m2 + atom_type_embed_nchanl,
hidden_size=fitting_hidden_size,
output_size=1,
activation_function=activation_function
)
ここでは、原子$i$の周りの環境を表す特徴量ベクトルを入力して、原子$i$のもつポテンシャルエネルギー$E_i$を予測するためのニューラルネットワークを定義しています。
input_sizeはm1 * m2 + atom_type_embed_nchanlで、m1*m2は原子$i$の周りの環境を表す特徴量ベクトルの大きさです。これに追加して、原子$i$のタイプの情報を一緒に入れたいので、$i$のタイプのEmbedding後の特徴量ベクトルを一緒に入れます。
DeepPotSEModelのforwardについて
はじめにforwardの引数を説明します。
coordsは全原子の座標$R$を表し、shapeは[N, 3]です。
atom_typesは全原子のタイプを表し、shapeは[N]です。
atom_i_idxsは原子$i$のindexが入ったベクトルで、shapeは[N*sel]です。
jを0 <= j < selとして、atom_i_idxs[atom_i_idx + j]にはatom_i_idxが入っています。
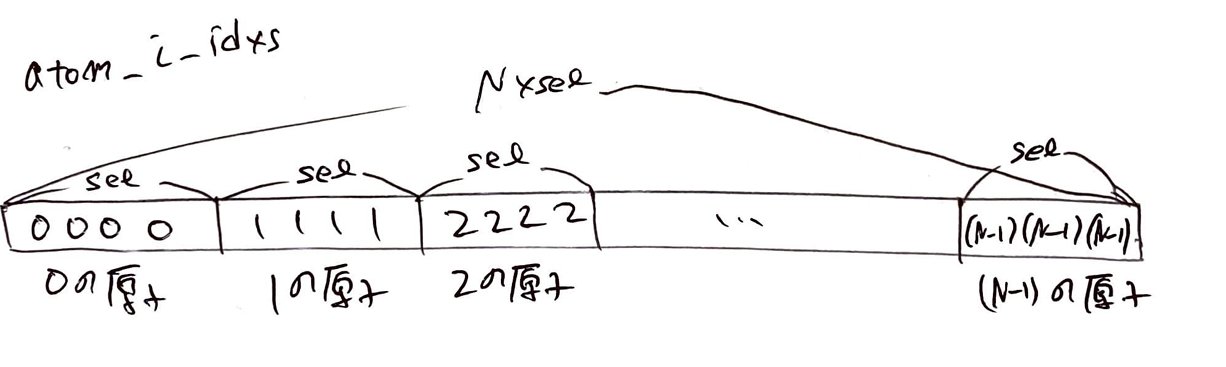
atom_j_idxsは原子$i$からみた原子$j$のindexが入ったベクトルで、shapeは[N*sel]です。
jを0 <= j < selとして、atom_j_idxs[atom_i_idx + j]にはatom_j_idxが入っています。下の図の例だと、atom_i_idxが1の原子の周りにはatom_idxが3, 2, 8, 5の原子があります。また、iの周りにsel個未満の原子しかない場合は、残りの部分はNで埋められます。
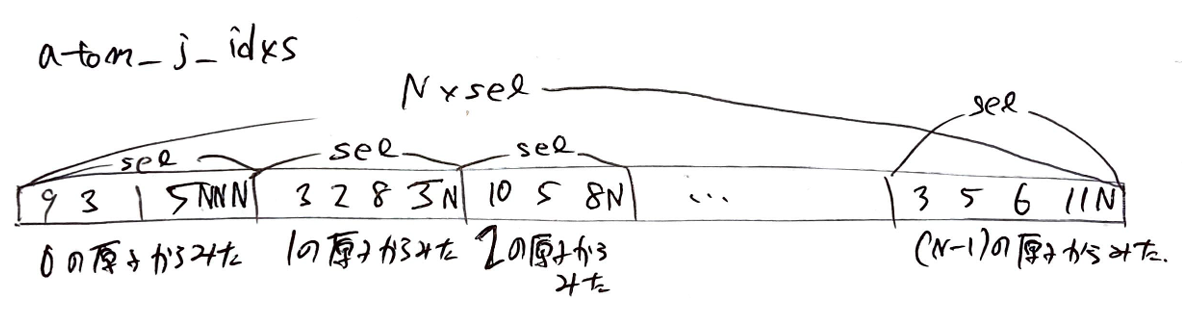
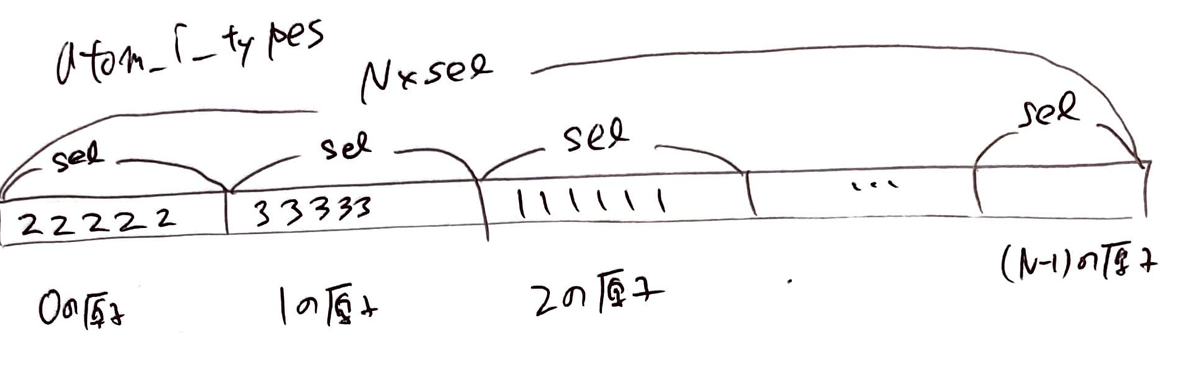
atom_i_typesは原子$i$のタイプの情報が入っているベクトルで、shapeは[N*sel]です。
jを0 <= j < selとして、atom_i_types[atom_i_idx + j]には原子iのタイプが入っています。下の図の例だと、atom_i_idxが1の原子のタイプである3で埋まっています。
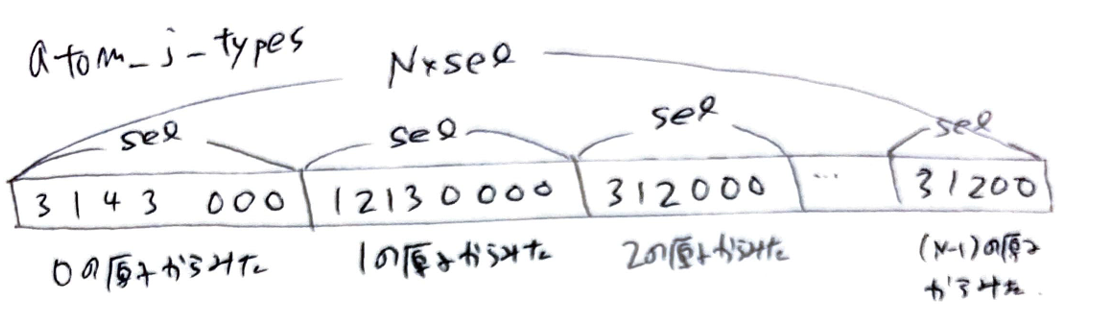
atom_j_typesは原子$j$のタイプの情報が入っているベクトルで、shapeは[N*sel]です。
jを0 <= j < selとして、atom_j_types[atom_i_idx + j]には原子jのタイプが入っています。下の図の例だと、atom_i_idxが1の原子の周りには、原子のタイプが1,2,1,3の原子があります。原子がない場合は0で埋めます。原子のタイプは、1から始めており、原子のタイプが0の原子は存在しないものとしています。
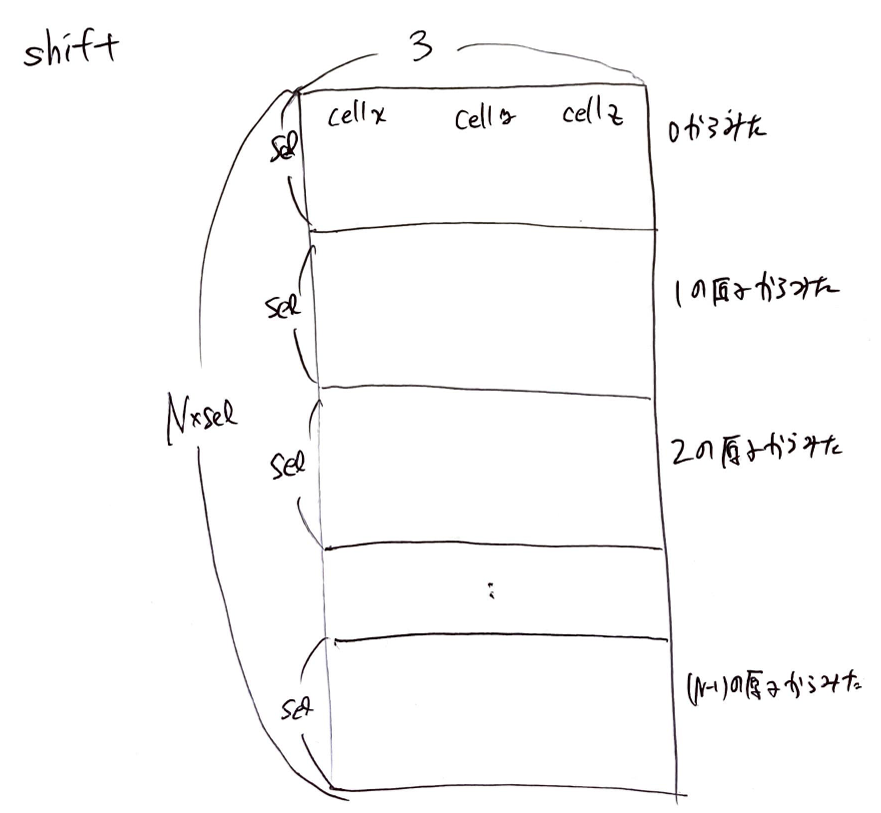
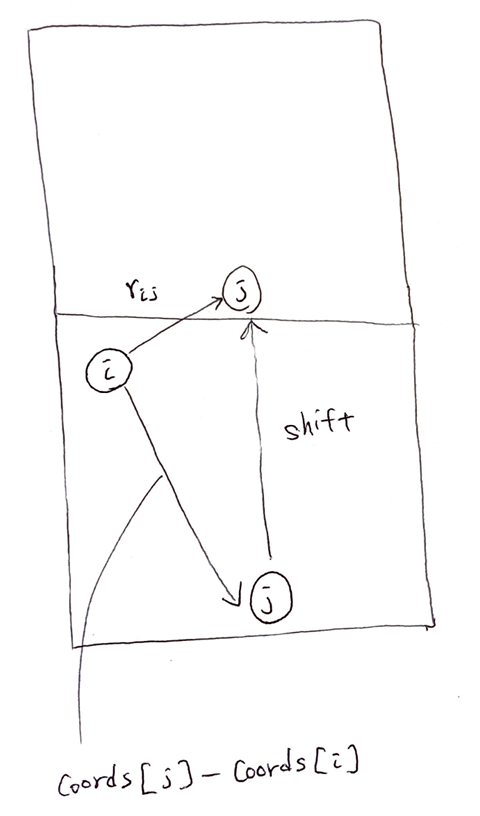
shiftは原子jがどれくらい周期境界によってシフトしているかを表す行列で、shapeは[N*sel, 3]です。なぜshiftが必要かというと、原子iからみた原子jの周期境界を考えたときの方向ベクトルは単純にcoords[atom_j_idx] - coords[atom_i_idx]にはならないからです。
原子jをセルの長さ分ずらすようなベクトルをshiftとすると、
原子iからみた原子jの方向ベクトル$r_{ij}$は
coords[atom_j_idx] + shift - coords[atom_i_idx]
として求めることができます。
引数の説明が終わったので、forwardの中を説明します。
coords.requires_grad_(True)
ここでは、最終的に、ポテンシャルエネルギーを位置(coords)で微分することで力を求めるため、requires_gradをTrueにしておきます。
relative_coords = self.coords_to_relative_coords(
coords=coords,
atom_i_idxs=atom_i_idxs,
atom_j_idxs=atom_j_idxs,
shift=shift,
)
ここでは、$R$(coords)を$R_i$(relative_coords)に変換しています。
def coords_to_relative_coords(
self,
coords:torch.tensor,
atom_i_idxs:torch.tensor,
atom_j_idxs:torch.tensor,
shift:torch.tensor,
):
coords_concat = torch.concat((
coords,
torch.full((1, 3), 1e5)
), dim=0)
relative_coords = coords_concat[atom_j_idxs] - coords_concat[atom_i_idxs] + shift
return relative_coords
coords_concatでは、coordsの一番下に十分大きな値を入れておきます。
相対座標は先程説明したように、coords_concat[atom_j_idxs] - coords_concat[atom_i_idxs] + shiftで求めることが出来ます。
generalized_coords = self.relative_coods_to_generalized_coords(
relative_coords=relative_coords,
r_cutoff=self.r_cutoff
)
def relative_coods_to_generalized_coords(
self,
relative_coords:torch.Tensor,
r_cutoff:float
)->torch.Tensor:
generalized_coords = torch.full((relative_coords.shape[0], 4), 1e2)
r_ij_norm = torch.linalg.norm(relative_coords, dim=1)
s_vec = smooth_cut_s_function(
r_ij_norm=r_ij_norm,
r_cutoff=r_cutoff
)
generalized_coords[:,0] = s_vec
generalized_coords[:,1:] = relative_coords * s_vec.view(-1, 1) / r_ij_norm.view(-1, 1)
return generalized_coords
def smooth_cut_s_function(
r_ij_norm:torch.tensor,
r_cutoff:float,
)->torch.tensor:
"""DeepPot-SE function s(r_ij) of tensor version
As r_ij becomes larger than r_cutoff_smth, the output of the function begins to decrease,
and as more r_ij becomes larger, the output of the function smoothly becomes zero.
Parameters
----------
r_ij_norm : torch.tensor
shape : (Coordination Num of atom i,)
r_cutoff : float
cutoff
Returns
-------
s_vec : torch.tensor
shape : (Coordination Num of atom i,)
"""
r_cutoff_smth = 0.1
s_vec = torch.zeros_like(r_ij_norm)
flag = (r_ij_norm <= r_cutoff)
u = (r_ij_norm[flag] - r_cutoff_smth) / (r_cutoff - r_cutoff_smth)
s_vec[flag] = (u*u*u*(-6*u*u + 15*u - 10) + 1) / (r_ij_norm[flag])
return s_vec
ここでは、$R_i$(relative_coords)を$\hat{R_i}$(generalized_coords)に変換しています。スイッチ関数は論文とは違うものを用いました。多項式の方が手で微分しやすいので、多項式のスイッチ関数を用いました。
"DPA-1: Pretraining of Attention-based Deep Potential Model for Molecular Simulation"という論文と同じスイッチ関数を用いています。
atom_type_one_hot = torch.eye(self.max_atom_type + 1)
atom_type_embedded_matrix = self.atom_type_embed_net(atom_type_one_hot)
ここでは、原子のタイプのワンホットベクトルをバッチ処理によって、embeddingしています。atom_type_embedded_matrix[atom_type]には、atom_typeをembeddingした特徴量ベクトルがはいっています。
s_rij = generalized_coords[:,0].reshape(-1, 1)
atom_i_embedded_matrix = atom_type_embedded_matrix[atom_i_types]
atom_j_embedded_matrix = atom_type_embedded_matrix[atom_j_types]
g_i1s_before_embed = torch.concat((
s_rij,
atom_i_embedded_matrix,
atom_j_embedded_matrix,
), dim=1)
ここでは、$s(r_{ij})$をembeddingする前処理をしています。
$s(r_{ij})$、原子iのatom type embeddingと原子jのatom type embeddingを
g_i1s_before_embedにしています。
g_i1s = self.embed_net(g_i1s_before_embed).reshape(coords.shape[0], self.sel, self.m1)
generalized_coords = generalized_coords.reshape(coords.shape[0], self.sel, 4)
ここでは、g_i1s_before_embedをバッチ処理によってembeddingし、shapeを[N, sel, m1]に変えています。
また、generalized_coordsのshapeを[N, sel, 4]に変えています。
# g_i1^T @ generalized_coords
left = torch.bmm(
torch.transpose(g_i1s, 1, 2),
generalized_coords
)
# generalized_coords^T @ g_i1[:, :m2]
right = torch.bmm(
torch.transpose(generalized_coords, 1, 2),
g_i1s[:, :, :self.m2]
)
D_i_s_reshaped = torch.bmm(left, right).reshape(coords.shape[0], self.m1 * self.m2)
ここでは、論文の
$$D_i = (g_{i1})^{T} \hat{R_i} \hat{R_i}^{T} g_{i2}$$
という部分で、N個の原子の$D_i$を同時に計算しています。
feature_vectors = torch.concat((
D_i_s_reshaped,
atom_type_embedded_matrix[atom_types]
), dim=1)
total_potential_energy = torch.sum(
self.fitting_net(feature_vectors)
)
最後に、$D_i$をreshapeして、原子$i$のatom type embeddingを一緒にしてfitting netに入れることで、ポテンシャルエネルギーを予測しています。
model = DeepPotSEModel(...)
total_potential_energy = model(...)
forces = -1 * torch.autograd.grad(
total_potential_energy,
coords,
)[0]
とすることで、それぞれの原子にかかる力を求めることが出来ます。
精度
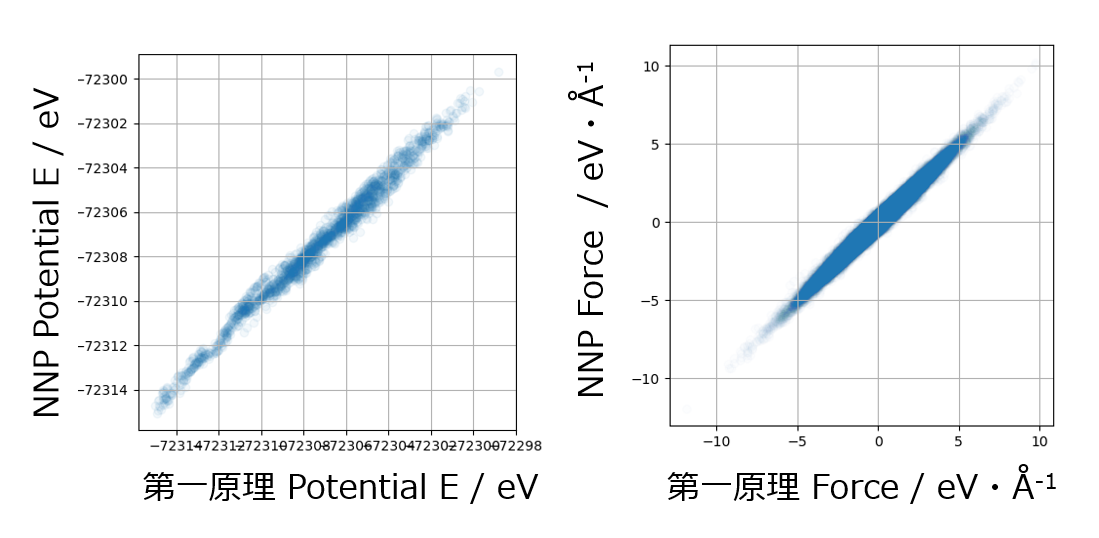
学習させたものは、密度が1の水分子で、学習に用いていないものをプロットしました。横軸に第一原理計算の結果、縦軸にDeepPot-SEで予測した結果をプロットしました。きれいに予測できていることがわかります。
最後に
forward中にfor文が入ってしまうと、遅くなってしまうため、
なるべくpytorchの関数をうまく使うのが難しかった。