宇宙際タイヒミュラー理論で量子エンタングルメントを扱えないだろうか？

注意事項
キャプチャーした画像の内容に関する著作権は、すべて引用元のサイトにございます。

Linked Ideal代表社員の久保寺です。~~Nextremerの久保寺です。Disruptive Tech. R&Dという研究部門の統括をしております。Disruptive Tech. R&Dでは、量子コンピュータの活用や自然言語処理などの研究を行なっております。~~今回は、**あくまでジャストアイデア**なのですが、量子エンタングルメントと宇宙際タイヒミュラー理論って相性いいんじゃないのか？とふと思い、何故そう思ったのかを記事にしてみたいと思います。出来るだけ補足を入れてなるべく理解が繋がるように努め、その結果少々長くなってしまいましたが最後までお付き合いいただければ幸いです。

望月新一氏のHP「宇宙際タイヒミューラー理論の拡がり」よりイメージ図

#そもそものきっかけ
以前弊社に来ていた大阪大学の博士課程のインターンの方が「量子情報専攻の学生が論理学を学ぶ理由」というタイトルの資料を作ってくれました。その中で論理学には「実数をどう表現すべきか」、「不完全性定理の壁」などの限界があり、それらに対して様々なアプローチがあり、論理学ではないですが既存の数学の枠を超えた考え方として、宇宙際タイヒミュラー理論にも言及されてました。当時は全く話に付いて行けずに「よくわからないけど何かスゴそう」とだけ思い、その後時間とともに記憶から消えてました。

ところが最近「宇宙と宇宙をつなぐ数学 IUT理論の衝撃」という本を読んだ事がきっかけで、そう言えばそんな理論について語っていた学生がいたなーと思い出したのです。IUT理論とは宇宙際タイヒミュラー理論のことです。下記がその本です。

https://www.amazon.co.jp/&tag=tonejiten-22/dp/404400417X/

ちなみにこの本の内容に付いて著者である加藤文元氏が説明しているYouTube動画もあり、大変わかりやすいです。ご興味ある方は是非、ご覧ください。

abc Conjecture and New Mathematics - Prof. Fumiharu Kato, Oct 7, 2017より

実際の理論は大変難しいらしいのですが、この動画を見て一つ思った事がありまして、それが量子エンタングルメントとこの理論は親和性が高いのでは？？？と感じたのです。何故そう思えたのか順を追って書いてみたいと思います。

宇宙際タイヒミュラー理論

上記の動画で**宇宙際タイヒミュラー理論により、数学上の難問の一つとされる「ABC予想」を証明できる**とのことです。ただし、宇宙際タイヒミュラー理論はABC予想に特化した考え方ではなく、数学に新しい視点を提供するものであるようです。加藤文元氏による動画説明をなぞりつつ、動画からの抜粋で簡単にその気持ちを４つ「ABC予想について」、「二つの絡み合ったものを別々に考える土台」、「入れ子の関係」、「対称性通信」に分けて追ってみたいと思います。詳しくは、動画の説明が大変わかりやすいのでそちらを見ていただけたらと思います。

ABC予想について

[ウィキペディアより](https://ja.wikipedia.org/wiki/ABC%E4%BA%88%E6%83%B3)

ABC予想は数学上の難問かつ2019年12月現在まだ未解決問題です。「まずABC予想がなんで難問なのか？」これについて動画でもわかりやすい説明がなされていますが、この問題の難しさポイントは、「a + b = c」 という足し算の話と「積abcの素因数の積d」というかけ算の話を比べようとしていることにあるようです。すなわち、足し算とかけ算という小学生でも理解できる話なのに、実は非常に奥深い複雑なバックグランドが存在して、その複雑さ故に、難問になっているらしいのです。０に1ずつ足して行くとすべての自然数が足し算によって得られますが、この中に含まれる素数という概念はこれだけからは導けません。素数はかけ算から素因数分解と通してその概念が生まれてきます。でもその素数という数は足し算の世界で意図せず作り出せてしまうのです。足し算の世界だけで考えているのに、意図せずかけ算の概念のモノが混入してしまう辺り、足し算とかけ算が何か絡み合ってる感じがします。そして素数がどのように分布しているのかすら2019年12月現在、まだ未解決問題なのです（リーマン予想）。問題の不等式はの左辺は足し算の話で、不等式の右側はかけ算の話になっているので、本来別々に扱いたいところですが、非常に奥深い複雑な関係性のために通常の数学の上ではそれがやりにくく、比較がしにくいという風に私は理解しました。すなわち、新しい数学の土台を設けてみようという発想にもなるわけです。

二つの絡み合ったものを別々に考える土台

ABC予想は、足し算とかけ算の背景に実は非常に奥深い複雑なバックグランドが存在し、それが問題を難しくしているのでした。ならばそれを分離して議論をする数学の土台を設けたら良いという発想は自然だと思います。ただし、いきなりその土台を思いつくのは、どんな天才にでも難しいでしょう。これまで築きあげた数学の中でその考え方の肥やしになるようなものに一旦目を向けるのは自然な一つの考え方です。そのような状況下で、望月氏が一つ注目したのはタイヒミュラー空間論ということなんだと思います。元々のタイヒミュラー空間論は、1次元複素数に対する理論らしいのですが、それですら大変難しく理解が追いつかないです。恐らく複素数における何か二つの対象に対して、片方だけを操作して議論できる便利な空間と思って一旦先に進みます。ABC予想では足し算とかけ算の一方だけを操作したい訳ですが、通常の数学の舞台では足し算とかけ算は同時に両方できてしまいます。そこにタイヒミュラー空間論を持ってきて片方だけを変形したいわけですが、元々のタイヒミュラー空間論は1次元複素数に対する理論でした。ここに何を持ってきたら、足し算とかけ算を別個に扱えるようになるのでしょうか？足し算とかけ算という数学上の根源的なものを扱う以上、数学一式ができるようなものに拡張する必要があります。数学では便利な考え方があって、一通り数学ができる舞台をユニバースと呼ぶそうです。そのユニバースを複数持ってきて理論を別個に展開させることができたとします。そうするとユニバースとユニバースの間のタイヒミュラー空間論という表現に落ち着きそうです。でもちょっと長いですよね。「国際」という言葉が「国と国の間の関係」を表すのと同様に、複数の数学の舞台すなわちユニバース同士の関係をユニバース際＝宇宙際として表現してやれば、宇宙際タイヒミュラー理論が言葉上は繋がります。これを一旦、二つの絡み合ったものを別々に考える土台と考える事にします。

入れ子の関係

当初の問題設定から非常に複雑に絡まりあった二つの対象（ABC予想では足し算とかけ算）を別々の舞台で扱う準備ができました。そして最終的には別々の舞台で扱った議論を比べることになります。でも単純に比べられるわけがありません。何かを比べるには、共通のモノサシが必要なわけです。例えば、距離を測るにもマイル、ヤード、尺と色々あるわけです。要は別々の舞台で構成されたもの同士はそもそもスケールが違うわけです。ここからさらに想像を逞しくしましょう。さらに拡張して、ヒトの人生について考えてみましょう。この状況を上記動画の中では、女優さんの例で説明していました。

上記の画像は、ある女優さんの通常の生活と、映画の中の女優さんだそうです。勿論同一人物な訳ですが、僕らはリアルな女優さんとは握手することができるかもしれませんが、映画の中の女優さんはスクリーン上の世界ですので握手はおろか、映画の中の彼女に本人ですらコンタクトする手段を持ち得ません。でも紛れもなく、同一人物であり、映画の中の彼女は、彼女の人生という中の1シーンとして演じた作品の中の彼女です。すなわち彼女の人生という舞台の中で、入れ子の構造ができているわけです。こういった構造の中で共有できる情報というのは意外と少ないということもわかります。映画の舞台では、名前すら本人と違うわけですから。この入れ子の構造の中で、何が同じで何が違うのかを測るモノサシはどのように設計すべきなのでしょうか？そこに一つの示唆を与えるのがIUT理論（宇宙際タイヒミュラー理論）なのですが、上記動画では面白いトリックを使って説明されていました。

動画の抜粋	補足
	入れ子の状況を作る
	一つの舞台だけではピースがはまらない
	入れ子の構造ではスケールが合えばハマる
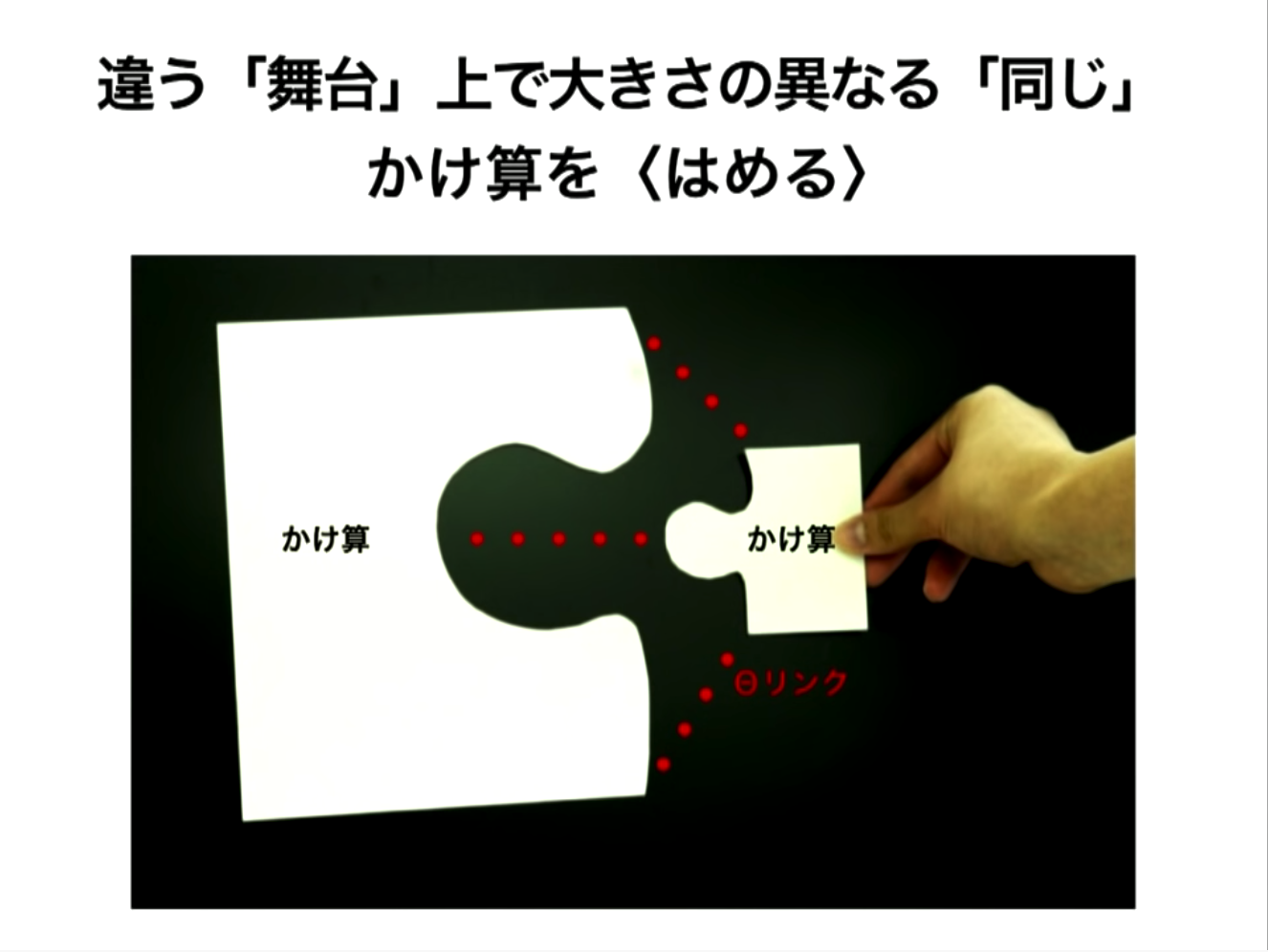	ABC理論におけるはめ方
	舞台が違うので歪みが出る
	歪みの大きさを定量化

対称性通信と復元

入れ子になっている構造の中で共有できるものは意外と少ないのでした。それではその中で何が共有できると考えれば良いのでしょうか？入れ子の関係をもう一度よく見てみましょう。

上記の例で言うと入れ子の中のピースは、大きさが異なっているのでピースがハマる舞台とそうでない舞台があるようです。すなわち縮尺という情報を与えてやれば良いわけです。ここからヒントを得て入れ子の中にもし同じと評価されるものが存在するならば、何かしらの変形の方法というものを伝えてあげれば、異なる舞台間のものが同じなのか、同じでないならどのくらい違うのかを舞台間の通信により知ることができます。
ただし、モノは通信してテレポートできません。数学では何か数学的対象に対して、ある操作を行った時にその数学的性質が保たれている場合は、対称性があると考えます。ここから拡張させてモノは通信でテレポートできませんが、モノにまとわりついている対称性を伝えることはできそうです。そこで異なる舞台間で何か数学的対象を対称性という情報をやり取りして、その情報を受け取った側で復元できるかということを考えてみるのです。具体例がないとピンと来ないのですが、動画では下記のようなわかりやすい具体例で説明が与えられていました。

動画の抜粋	補足
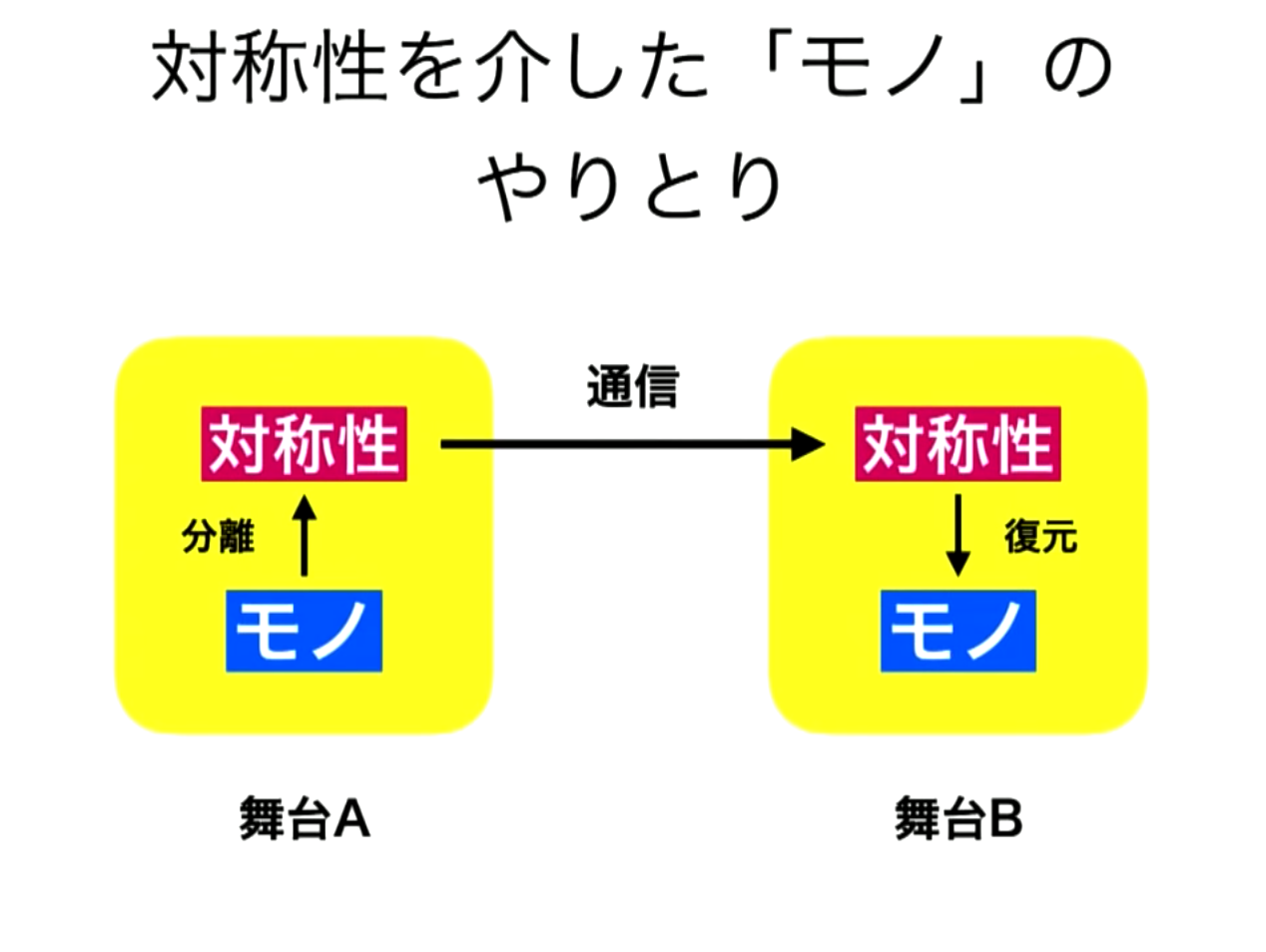	異なる舞台間モノはテレポートできないがモノに宿っている対称性は伝えることができる
	異なる舞台間で三角形というものを対称性という情報で伝えて復元できるか考える
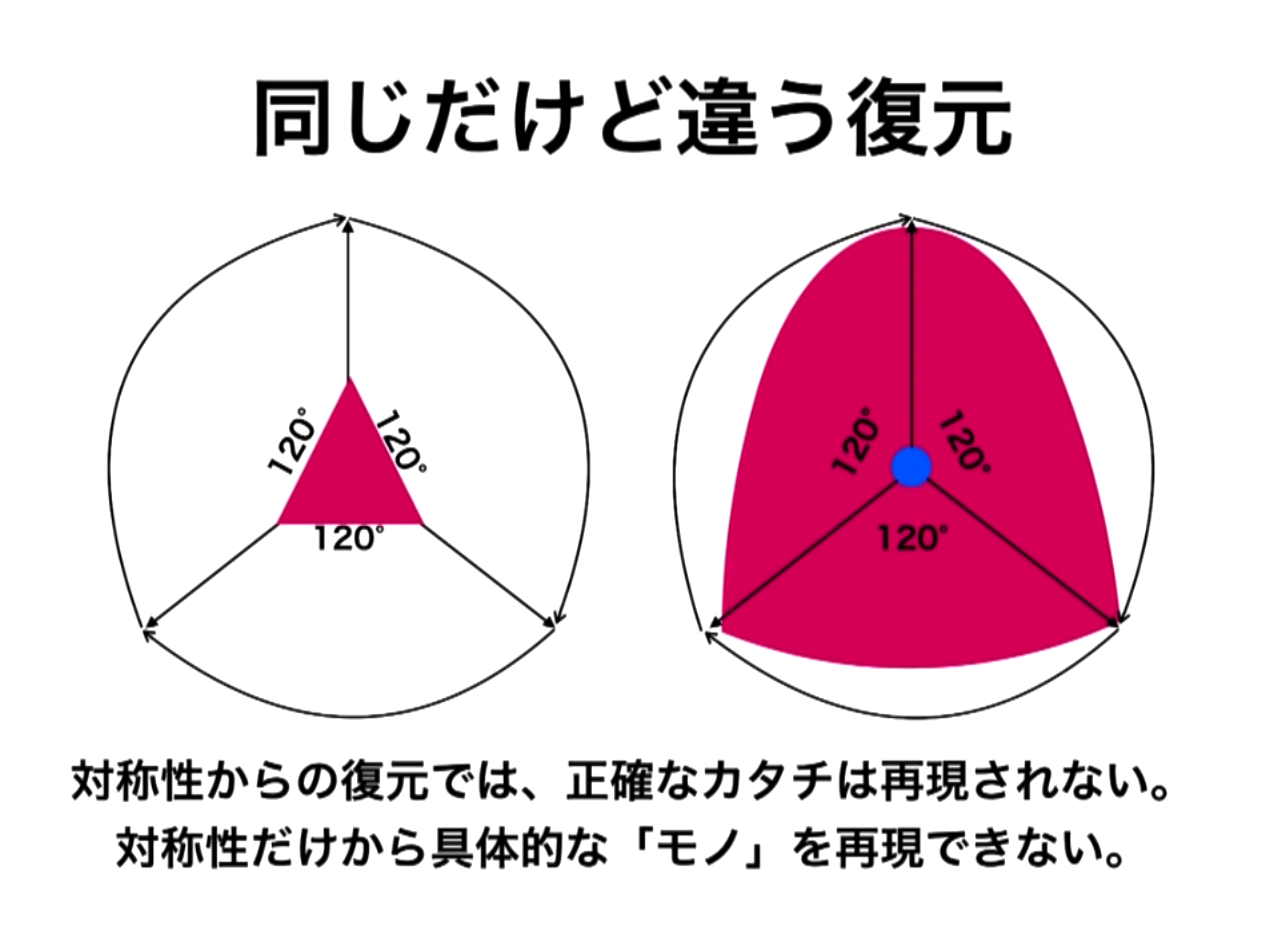	対称性が複雑でないと完全には復元できない
	円は相似形を除いて完全に復元できる。すなわち円は複雑な対称性を持っている？

以上、ここまでで大変長くなってしまいましたが、宇宙際タイヒミュラー理論についての加藤文元氏の説明動画を部分的に追ってみました。

量子エンタングルメント

量子エンタングルメントは「量子もつれ」とも呼ばれてまして、私達の住む世界の直感とは、かなりズレた量子の世界の性質の一つです。最近は何でもわかりやすい説明がYouTubeに上がっていてありがたいですね。量子エンタングルメントもわかりやすい動画がありました。

量子エンタングルメントは、横柄に言ってしまえば、複数の粒子が相互作用を持ったとき、その粒子達をどれだけ引き離してもその相互作用が保持される現象です。いくら粒子であっても光の速度を超えて通信はできないので、どのようにこの相互作用が保持されているのかは非常に議論のある問題で、かのアインシュタインも「奇妙な相互作用」と言った程です。

量子エンタングルメントは量子情報科学という分野で、古典の情報理論であるシャノンの情報理論をアレンジしてその量子版の定量化が研究されてきました。

古典の情報理論と量子情報理論の対応

シャノンの情報理論	量子情報理論
情報エントロピー	フォンノイマンエントロピー
ダイバージェンス	量子相対エントロピー（梅垣エントロピー）
相互情報量	Holevo情報量

そして特定の条件化では、エンタグルメントの定量化の指標も定義されました(例：Peres基準)。
ただし、多体間のエンタングルメントの定量化および包括的な理論は未だこの分野の未解決問題なのだそうです。この非常に難しそうな問題なのですが、不思議と宇宙際タイヒミュラー理論のコンセプトと符号する点があります。その辺りを最後に次のセクションに書いてみたいと思います。

#宇宙際タイヒミュラー理論と量子エンタングルメントとの相性？
さて、やっとここで本題の議論になる訳ですが、あくまでジャストアイデアなのでそこだけお含みおきいただいてお読みいただければと思います。量子エンタングルメントの性質をうまく応用した例として、量子テレポーテーションがあります。量子情報科学の分野の大原則で「量子状態は、コピーする事ができない」という定理があります。No-Cloning Theoremと言います。量子状態がコピーできないのに通信して相手に量子状態を送れてしまうのが量子テレポーテーションです。
量子テレポーテーションは、量子エンタングルメントの性質を使って、送信元の量子状態を通信して、送信先で復元する仕組みです。まず量子エンタングルメントした粒子を用意します。それを離れた二人でそれぞれ１個ずつが持ちます。下記の図では、「B」と書かれているものです。そして「秘」と書かれているものが復元したい量子状態になります。リノちゃんはこの量子状態と「B」を使ってあるオペレーションをし、観測をします。観測をすると量子状態は壊れてしまいますので、この時点でリノちゃんが持っていた「秘」は壊れてしまします。リノちゃんはその観測結果をニュー君に伝えます。伝える手段は何でも良いのですが下図では電話を使ってます。ニュー君は、電話で伝えられた情報を元に「B」にオペレーションを施し、リノちゃんが持っていた量子状態を復元します。一度壊れてしまった量子状態が量子エンタングルメントによって復元できたことになります。

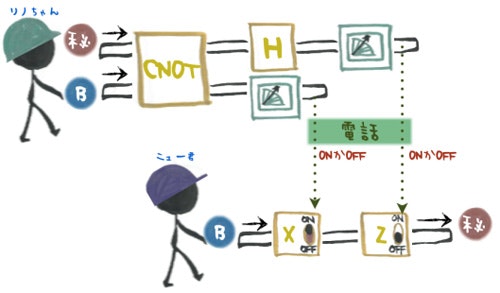[ガジェット通信「中学レベルの数学で量子テレポーテーションを理解してみよう」より](https://getnews.jp/archives/404198/4)

私が、宇宙際タイヒミュラー理論のコンセプトと量子エンタングルメントの定量化が大きく符号すると思う点は下記の３つです。

宇宙際タイヒミュラー理論のキーポイント	ABC予想の場合	量子テレポーテーションの場合
複雑に絡み合っている関係	足し算とかけ算の関係	量子エンタングルメント
対称性通信	楕円関数による対称性	圏論上の随伴という構造
復元	かけ算の構造を復元する	量子状態を復元する

量子エンタングルメントは、粒子と粒子がもつれて奇妙な相互作用を持つ現象ですので、複雑に絡み合っている関係そのものです。そして量子テレポーテーションには通信によって復元というプロセスもあります。ただし、量子テレポーテーションの上図からは対称性らしきものが見えません。その辺りを説明したいと思います。

量子テレポーテーションという現象に対して、圏論という数学を使用して説明を試みた論文Introducing categories to the practicing physicisがあります。Oxford大学のBob Coecke氏によって書かれたものです。

Bob Coecke氏によれば、圏論において量子テレポーテーションは、「随伴」という構造で説明ができるそうです。そのことを絵算を使って説明しています。絵算では、計算に必要なパーツを絵で表現して計算の仕方は絵の繋がり方をルールとして与えて計算して行きます。

まずエンタングルした状態を下三角から二つの足が出ている図で表現しています。

ここでさらに「随伴」という双対的な概念を導入します。双対とは、wikiによれば２つの事象が互いに「裏返し」の関係にあるようなニュアンスのものと説明されていますので、そのようなイメージのものだと一旦しましょう。

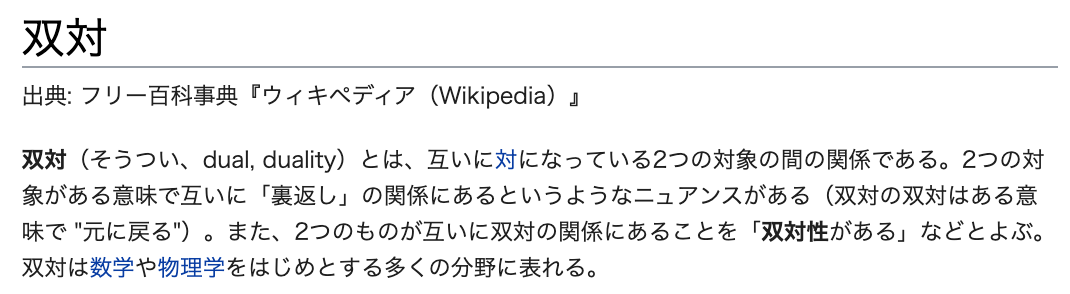
すなわちエンタングルメントという現象に対して、全てが裏返しになったような状態を考えてその双対的な対象同士の関係性を構造として捉えてやるわけです。一般に双対の双対をとると元に戻りますので、双対性は対称性に関連する性質でもあるのです。

量子テレポーテーションで復元したいものは、量子状態でしたので、これは「A」として与えます。
ルールは簡単です。矢印の向きが合うようにパーツを組み合わせるだけです。
Bob Coecke氏によれば、下記のように繋げると量子テレポテーションが表現できると主張しております。

量子状態「A」を用意して、エンタングルした状態とその随伴というシステムにより計算をすると（絵を繋げることに相当します）、量子状態「A」を移動させることができるわけです。このことを「yank」と著者は表現しており、ぐいっと引っ張って絡まりが解けることが量子テレポーテーションの一つの数学的な見方としています。

何か対称性を元に通信している感じが、少し感じていただけたでしょうか？ 私だけの妄想なのかもしれませんが、、、もし宇宙際タイヒミュラー理論の中の対称性通信の拡張版として随伴通信ということが実現できるのであれば、コンセプト的には量子テレポーテーションそのものであり、何となく量子エンタングルメントは宇宙際タイヒミュラー理論でも扱えるのでは！！？と思うわけです。

#まとめ
今回、宇宙際タイヒミュラー理論で量子エンタングルメントについて思うところを記事にしてみました。何度も繰り返しますが、**あくまでジャストアイデア**ですので、その点だけお含みおきくださいませ。宇宙際タイヒミュラー理論は、改めてきちんと勉強してみたいです。
その時にこの記事を振り返って、何かまた書けそうであればシェアしたいと思います。今回、大変長い記事になってしまい恐縮です。最後までお読み頂きありがとうございました。