Linked Ideal代表社員の久保寺です。~~Nextremerの久保寺です。Disruptive Tech. R&Dという研究部門の統括をしております。Disruptive Tech. R&Dでは、量子コンピュータの活用や自然言語処理などの研究を行なっております。~~今回は、トポロジカル量子コンピュータに関する記事を書きたいと思います。
#フォールトトレラント量子計算
フォールトトレラント量子計算とは、外乱があっても誤り耐性があり、正確に計算ができる量子計算という意味です。何故これが大事なのかということをまず説明したい思います。
通常のコンピュータでもビットすなわち0と1を表現するものが必要ですが、量子コンピュータでもそれに対応するものでさらに量子性を有する、量子ビットを実現するものが必要になります。現在注目されているのは超電導量子ビットやイオントラップ型の量子ビットです。ただし、問題はこの量子ビット数のスケーラビリティーです。2019年12月現在オフィシャルに報告されたもの中では、Googleが発表した72量子ビットが実現できた最高の量子ビット数です。量子ビットのスケーラビリティーを高めていく技術は、ハードルが非常に高く日進月歩で研究されており、ちょっと昔は１００年経ってもできないだろうと言われていたそうです。ただし現状ここまで来てるわけでブレイクスルーが後いくつかあると汎用的な計算ができる規模になるかも！！と期待されているわけです。下の図は今後の量子ビット数の推移を予測したものです。
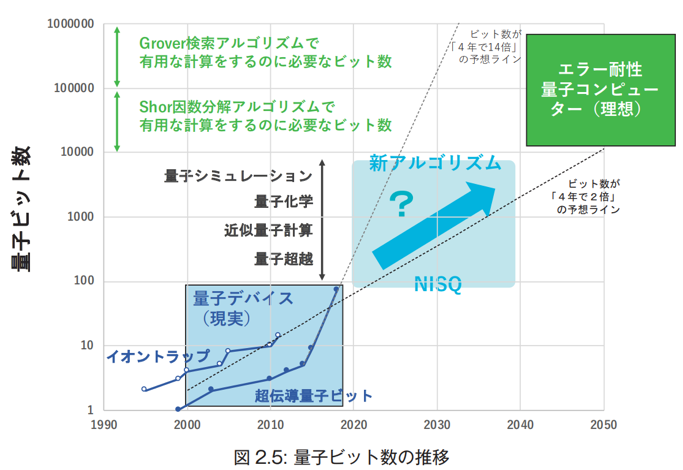
「戦略プロポーザルみんなの量子コンピューター（CRDS-FY2018-SP-04） 」より
そしてスケーラビリティーとは別にもう一つ大きな課題があります。それは量子ビットの誤り訂正です。量子ビットは、現在様々なタイプのものが研究されてますが、ほとんどの量子ビットが非常にノイズの影響を受けやすく、計算を正確に行うには誤り訂正が必要なのです。ノイズがあって誤りが発生しても正確な計算が行える量子計算をフォールトトレラントな量子計算と呼びます。その誤り訂正は補助の量子ビット使って行う方法が報告されています。よって、計算に必要な量子ビットの他に誤り訂正をするための補助量子ビットが必要で、これが計算に使用する1量子ビット（1論理量子ビット）よりさらに多くの補正量子ビットが必要なのです。
もし、量子ビット自体に誤り耐性を持ってくれていれば、この補助量子ビットはいらない、もしくは少なくする事ができます。実はそんな量子ビットの実現方法も研究されているのです。それがトポロジカル量子ビットという考え方です。今回この記事ではそのトポロジカル量子ビット（下記画像の右から２番目のタイプ）を使用した量子コンピュータの計算について書いてみたいと思います。
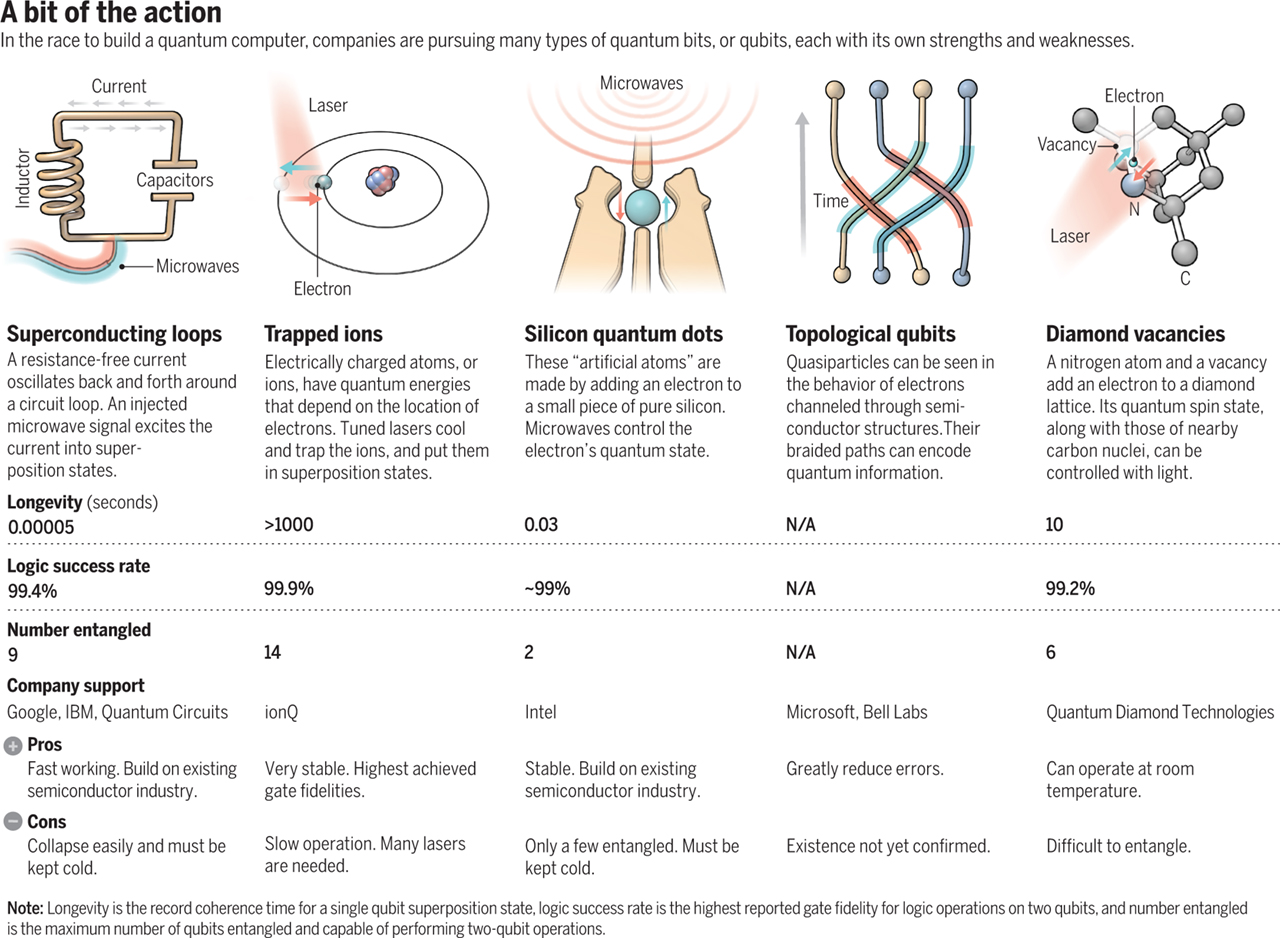
blog.usejournal.comの記事「Quantum Computing — The Basics, The Bad, and the Solution」より
#トポロジカル量子計算とは
トポロジカル量子コンピュータの最大のメリットの一つは、フォールトトレラントな量子計算が可能なことです。ただし、トポロジカル量子コンピュータに関しての理論はとても難しいです（少なくとも私にとっては）。そんな中、英語ですが、比較的わかりやすい説明をしているYouTube動画がありました。物理学者Steve SimonさんのCSSQI2012というサマースクールでの講義です。ご興味ある方は、是非ご覧ください。
Steve Simon - Topological Quantum Computing (Part 1) - CSSQI 2012
この記事では、このYouTube動画から抜粋してトポロジカル量子計算について簡単に追ってみたいと思います。まず、量子コンピュータを実現するリソースとして粒子のペアを考えます。
上記画像で真ん中やや左にTimeと書かれていてその右側に３枚の２次元平面があります。下から上に向かって時間が流れます。２次元平面には二つの粒子がある想定です。この粒子のペアが時間が経過して位置を交換したとします。３次元では粒子の統計性から二つの可能な時間発展ができます。一つは、粒子の位置を交換しても状態が変わらないもの（画像の中ではBosonsと書かれているもの）、もう一つは粒子の位置を交換すると状態にマイナスのサインがつくもの（画像の中ではFermionsと書かれているもの）です。それぞれ具体的には、光子と電子が対応します。ただし、不思議なことにこれを２次元の自由度しか持たないようにしてやり一定の条件を加えると、上記の二つとは違った挙動を示すようになります。それが下記の画像です。
上記画像の右下に書かれているUと表記されてるものは、数ではなくユニタリ行列というものになります。これは一体何が起きたのでしょうか？？？
量子状態（数学的にはヒルベルト空間上のベクトルに相当します）というものは、状態にユニタリ行列が作用する事で時間発展します。作用というのは、計算に相当するものだと思ってください。２次元＋特定の条件下にしてやると粒子が交換するだけで、状態にユニタリの作用がかかり、すなわち計算ができるのです。
そしてなぜこれがフォールトトレラントなのかというイメージを上記画像で説明しています。一般的にゲート型量子コンピュータでは、状態の時間発展を上記画像左側に示されているような量子回路という表記で示す事ができます。下から上に時間が流れる想定です。一方でこれと等価な時間発展がトポロジカル量子コンピュータでも可能です。これが上記画像の右側です。一般に量子コンピュータはノイズに非常にセンシティブで系に光子が一つ入っただけでも計算に影響が出てしまうので徹底的に遮蔽します。熱にもケアが必要なので絶対零度近くまで冷やすのが通常です。なので一般的にはチップを遮蔽して冷やす下記のような形状になります。
[IBMブログ記事「量子コンピューター「IBM Q システム」誕生の背景」より](https://www.ibm.com/blogs/think/jp-ja/ibmq-quantum-computer/)
ところでトポロジカル量子コンピュータは、粒子が交換した軌跡（world line:世界線と呼ばれたりします）が計算に相当します。上記の一個前の画像の右側の組み紐のようなものです。ここで計算の始めと終わりで粒子の位置さえ固定してしまえば、この組み紐に多少ショックを与えても、交わり方だけは時間ごとに刻まれていて変わりません。例えば、多少この系の現在の状態に何かショックを与えても端点を固定して位置を交換しないようにさえすれば、時間ごとに刻まれた交点数や絡まり方は不変にできます。多少雑ではありますが、これが多少系にショックを与えても計算が常に同じになる原理、すなわち誤り耐性のある計算が可能になる原理になります。動画では「TOPOLOGICAL PROTECTION」と説明されており、まさにトポロジカルな性質によって保護される計算ということになると思います。
#トポロジカル量子コンピュータと関連する分野
トポロジカル量子コンピュータは、非常に多くの分野と関連します。それは、理論構築に数学のオブジェクトを使用するのですが、その数学の世界が豊かだからかもしれません。特に組み紐のトポロジカルな不変量との関連から、結び目やその不変量であるジョーンズ多項式にも関連があります。また、そのジョーンズ多項式の不変量は、Chern-Simons理論から導くことができ、それと共形場理論との関係から、Ads/CFT対応というD+1次元のものをD次元で考えることのできる理論とも関連するそうです。先ほど、二次元平面の自由度の粒子に特定の条件を加えると特殊な物性が出ると説明しました。このような粒子としてマヨラナ準粒子というのが一つ注目されています。3次元でのマヨラナ粒子はまだ発見されておりませんが、２次元であればそういった粒子（準粒子といったり、エニオンと言ったりします）の物性を利用する事ができるかもしれないのです。３次元のものが２次元の物性に現れるという意味でAds/CFT対応の理論との繋がりがそれをサポートしているのかもしれません。
また、マヨラナ準粒子は実際にトポロジカル物質に出現する事が理論から予想されており、実際にその研究も物性物理の方で盛んに行われています。トポロジカルな物性の研究で有名な量子ホール効果、および分数量子ホール効果は、それぞれの仕事に対して過去ノーベル賞が付与されています。
1985年「量子ホール効果の発見」によりクラウス・フォン・クリッツィングがノーベル物理学賞受賞。
1998年「分数電荷の励起を持つ新しいタイプの量子流体（分数ホール効果）の発見」により、H. L.シュテルマー教授、D. C. ツーイ教授と共同でノーベル物理学賞受賞。
#まとめ
今回量子コンピュータの中でも異色なトポロジカル量子コンピュータの計算について非常に簡単にまとめてみました。今回、数理的取り扱いの説明は省きましたが、トポロジカル量子コンピュータは数理的にも大変面白く、勉強していて楽しい分野です。2019年12月現在、オフィシャルには、トポロジカル量子コンピュータの量子ビット実現の報告は一つもありません。ITモンスター企業の中ではマイクロソフト社が実現に向けて進めているそうです。早くまず１量子ビットができたという報告が聞きたいところです。
さて、ここで告知です。来年2020年1月から、このテーマでの勉強会（無料です）を開催しますのでご興味ある方は是非ご参加ください！
https://connpass.com/event/158742/
予定しているテーマ
| NO | 開催月 | 前半 | 後半 |
|---|---|---|---|
| 第1回目 | 2020/1/31 | ユニバーサルな量子計算 | トポロジカル量子計算の概要 |
| 第2回目 | 2020/2 | 具体的な量子アルゴリズム | トポロジカル物質について |
| 第3回目 | 2020/3 | 量子誤り訂正の基礎 | エニオンによる量子計算 |
| 第4回目 | 2020/4 | 表面符号について | 結び目と量子群について |
| 第5回目 | 2020/5 | Braidによる量子計算 | Chern-Simons理論について |
| 第6回目 | 2020/6 | 予備 | 予備 |
非常に多岐に広がるトポロジカル量子コンピュータの理論ですが、私たちも理論をまさに勉強中ですので、等身大の知識をまずシェアしてFBなど頂きながら知識をアップデートして行きたいと考えております。なので、勉強会などを通して、この方面に興味のある方、有識者の方と是非一緒に理解を深めていけたら幸いです。最後までお読み頂きありがとうございました。