スライドパズルをJavaScriptで自動解答させてみた

Last updated at 2025-04-25Posted at 2025-04-24

自分でパズル作ったけど、解けない( ﾟДﾟ)ってなったのでAIに解いてもらった

機能追加の背景

前回作った正式名称良く分からないパズルですが、
一瞬で解けることもあれば、
割と時間かかることもある、、、というか戻せないぞ、、これ戻せるの？
これ以上頑張るのは面倒だな、、というか、パズルなら数学的な解法があるのでは？
→やっぱりあるらしい！
ということで、アルゴリズムの理解はしきれなくても良いので、
取り敢えず実装してこのパズルを解いてもらおう。
AIと言っても、ゲーム用のスクリプテッドAIという感じです。
Scripted AI、流行りの「学習」とかではない。
実装、アルゴリズムに基づいて動く。という感じ。

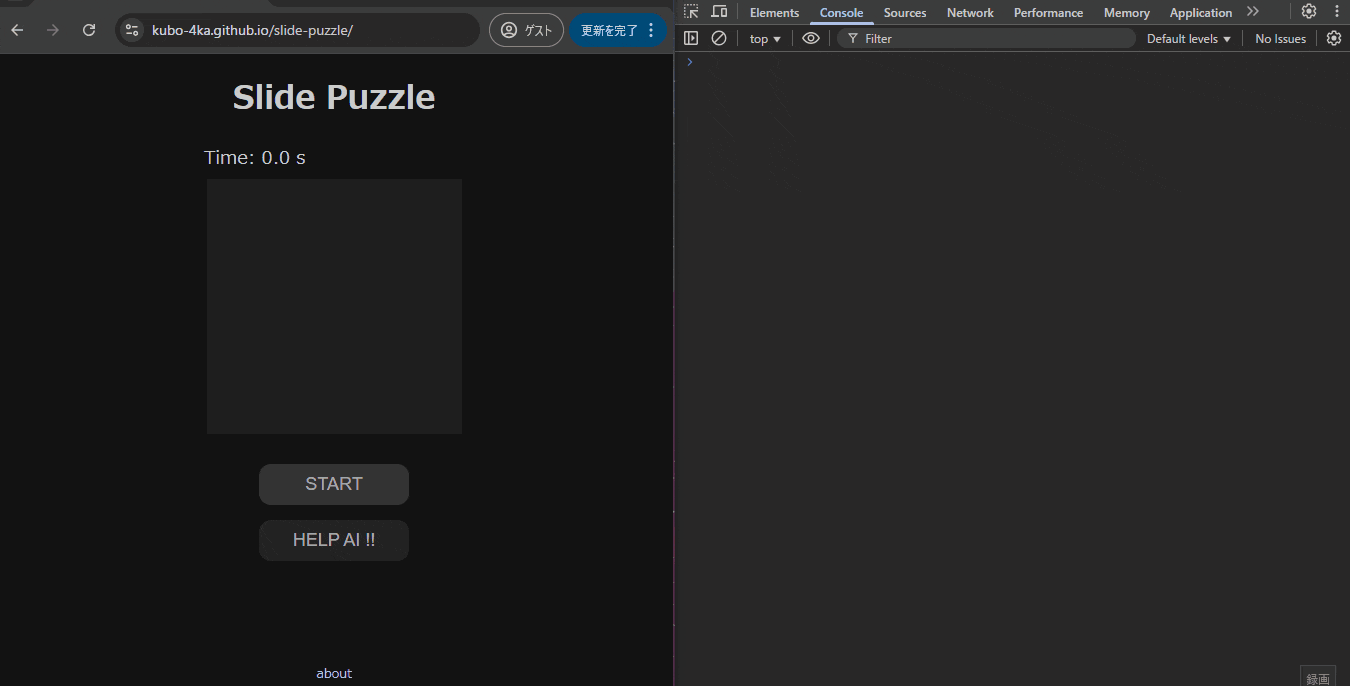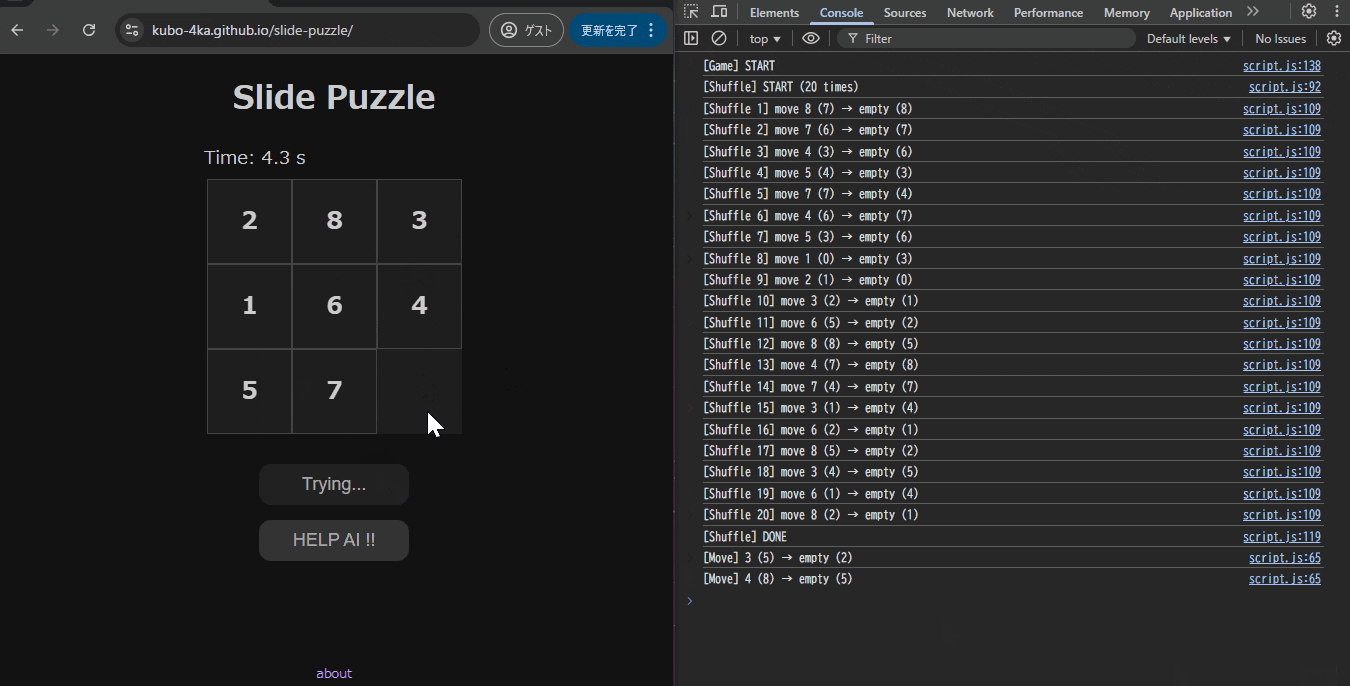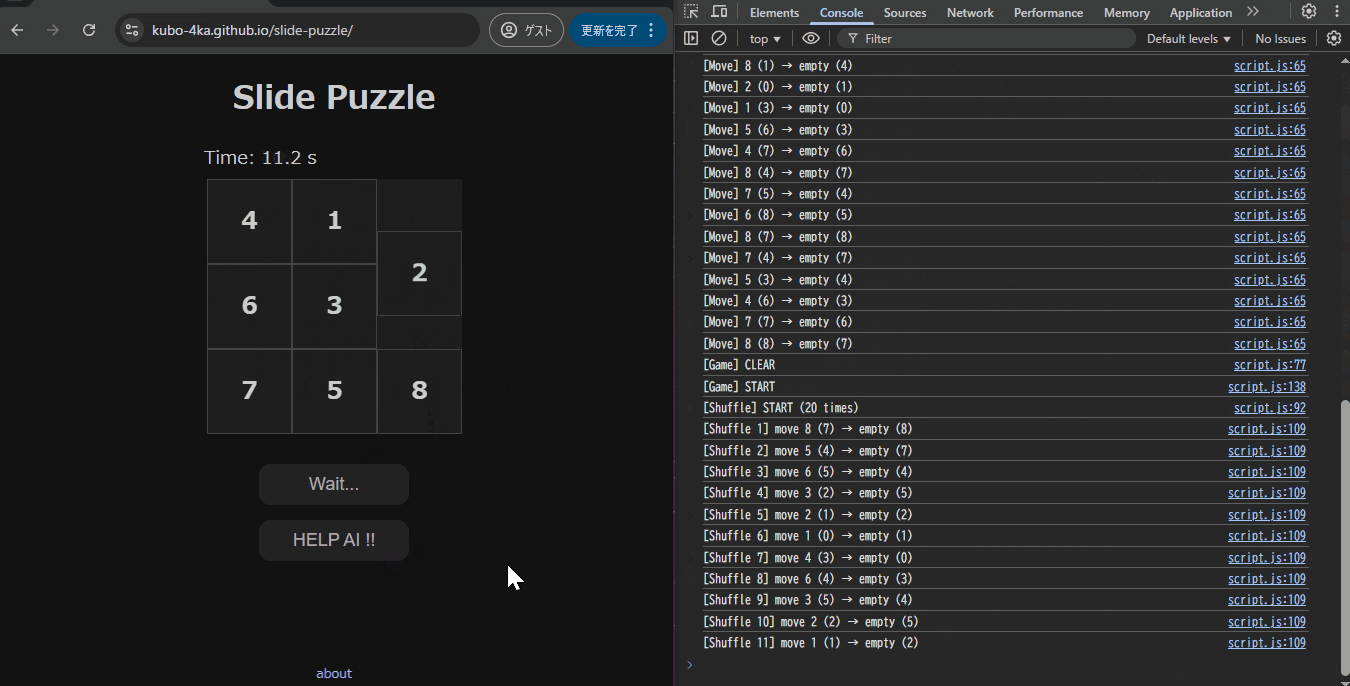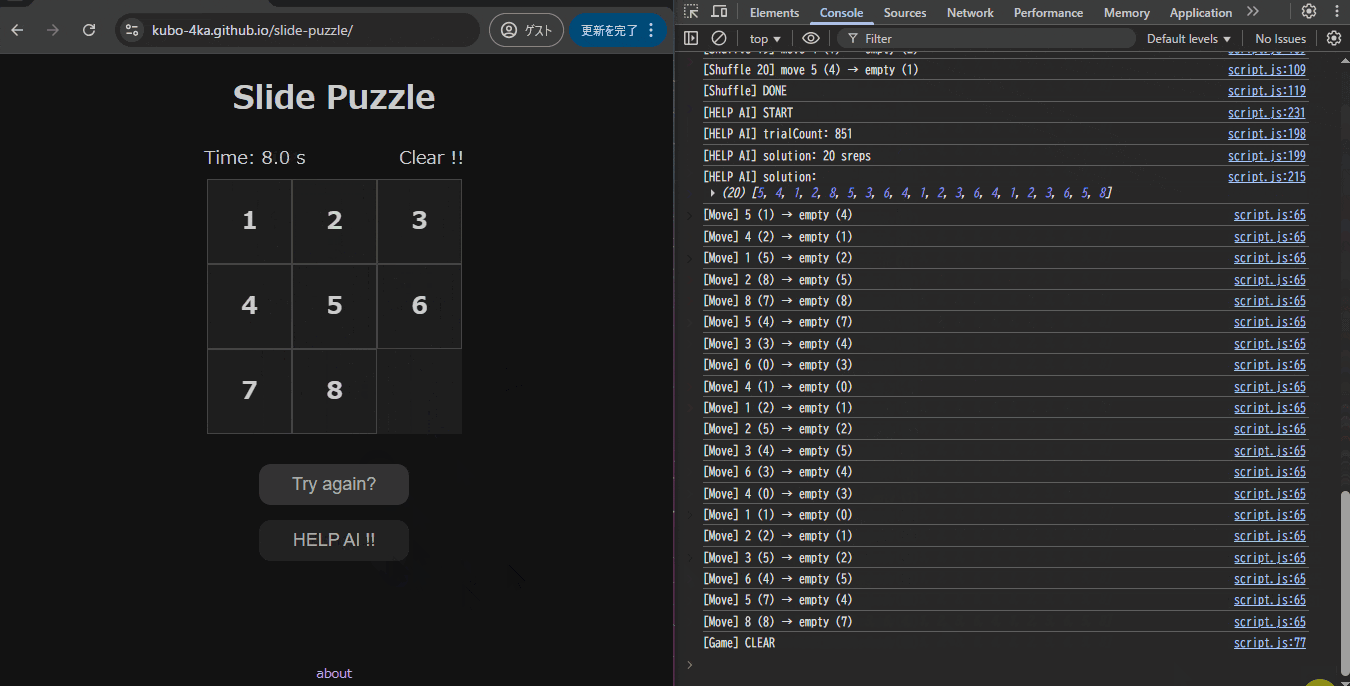
それでもログ見ると、一瞬で多い時は千以上の探索をしていて、
こりゃ叶わないな、凄いなと思いましたね( ﾟДﾟ)

デモ

ソース

前回記事

追加機能について

自動解答機能の処理説明（autoSolve）

autoSolve() の概要

この関数は、現在のスライドパズルの状態からクリアまでの最短手順を求め、一定間隔で1手ずつピースを動かすことで自動的に解答を完了させる処理です。

主な流れ

solvePuzzle() を呼び出し、現在の盤面（tiles）から最短手順を取得する。
setInterval によって、定期的に moveTile() を呼び出し、ピースを1手ずつスライドさせる。
最後の手が終わったら、showResult() を呼び、ゲームクリアの演出を行う。

使用される主な関数と役割

solvePuzzle(initialTiles)

A*アルゴリズムを使って現在の盤面からゴールまでの最短手順を探索する。
戻り値は「正しい順序で動かすべきタイル番号の配列」。

moveTile(num)　＃既存

指定されたタイルを空白の位置にスライドさせる関数。
自動・手動の両方から利用される。
解答が完了しているか（checkClear）もここでチェックされる。

showResult()　＃既存

パズルの完成を示す。
タイマーを止め、ボタンの表示や状態を更新する。
クリアメッセージを表示する。

フラグ制御

isAiSolving

自動解答中であることを示すブール値。
true の間、ユーザーの手動操作は無効化される（タイルクリックが無視される）。
自動解答が完了すると false に戻る。

利用タイミング

「HELP AI !!」ボタンが押されたときに autoSolve() が呼び出される。
この時点で isAiSolving が true になり、UI上ではスタートボタンが「give up...」、HELPボタンが「solving...」と表示される。

まとめ

autoSolve() は、ユーザーの代わりにAIがスライドパズルを解いてくれる自動解答機能です。A*アルゴリズムにより最短ルートを導き、1手ずつ丁寧に再生することで、ユーザーにとって直感的で納得感のある自動進行を実現します。

アルゴリズムについて

A*アルゴリズム（スライドパズル用）とは？

A*（エースター）アルゴリズムは、最短経路を探索するための代表的な探索アルゴリズムです。
スライドパズルでは、「現在の並び順」から「完成状態」へ到達するための最小の手数ルートを求めるために使われます。

基本の考え方

A*アルゴリズムでは、状態（ノード）ごとに以下の評価値 f(n) を計算して探索を行います：

f(n) = g(n) + h(n)

g(n)：スタートから現在の状態 n までにかかったコスト（手数）
h(n)：現在の状態 n からゴールまでの推定コスト（ヒューリスティック）

この f(n) が小さい順に探索を進めることで、効率よくゴールにたどり着くように設計されています。

スライドパズルでの適用

ステート（状態）

各ステップにおける tiles の並び（例：[1, 2, 3, 4, null, 5, 6, 7, 8]）

移動操作

空白（null）の上下左右にある数字をスワップすることで次の状態へ移動

ゴール状態

1 2 3 4 5 6 7 8 null の順番が完成形

ヒューリスティック関数 `h(n)` の設計

最も一般的なものは マンハッタン距離（Manhattan Distance）です。

マンハッタン距離とは？

各タイルが本来の位置から縦横にどれだけズレているかの合計：

h(n) = Σ |現在位置.x - 正しい位置.x| + |現在位置.y - 正しい位置.y|

この距離を8個のタイルに対して計算し、合計値を推定コストとします。

探索の流れ（簡略版）

初期状態を「オープンリスト（探索候補）」に追加
オープンリストから f(n) が最小の状態を取り出す
ゴールと一致していれば終了
可能な次の状態（隣接ノード）をすべて生成
それぞれの g(n)、h(n)、f(n) を計算してオープンリストに追加
上記を繰り返す

スライドパズルにおける利点

ゴールまでの最短手数が保証される（正しい順序で動かす）
完成形が固定されているので、状態の重複チェック（visited set）も容易
状態空間（9! = 362,880 通り）に対しても、ヒューリスティックにより現実的な速度で解ける

注意点

マンハッタン距離は有効なヒューリスティックだが、過小評価であること（楽観的） が条件
絶対にゴールを見逃さないため、h(n) は「実際の残りコストより大きくなってはいけない」

まとめ

A*アルゴリズムは、スライドパズルのような有限の状態遷移問題において、
・最短手数を求めたい
・無駄な手を避けて効率よくゴールしたい
といったニーズに非常に適した探索手法です。

スライドパズルにおいては、「完成までにどう動かすか」 を自動で導く頭脳となる、重要な中核機能です。

具体例の確認

スライドパズルにおける A* アルゴリズムとマンハッタン距離

そもそも「A*（エースター）」って？

A* アルゴリズムは、「最短の手数でゴールにたどり着く方法」を探すための頭のいい探し方です。

パズルでいえば、「一番少ない手で完成形にできる方法」をAIが計算してくれる感じです。

今回のパズルの完成形

完成形は次のように並んでいる状態です：

1 2 3 4 5 6 7 8 □（空白）

たとえば、こんな初期状態だとします：

2 8 3 1 6 4 7 □ 5

この状態から、A*アルゴリズムが「あと何手で完成できそうか？」を予測するために使うのが「マンハッタン距離」です。

マンハッタン距離とは？

マンハッタン距離とは、あるタイルが正しい場所に行くまでに必要な「上下左右の移動の回数」 を数える方法です。

実際に数えてみよう！

現在の並び：

[2, 8, 3, 1, 6, 4, 7, □, 5]

それぞれの数字の正しい場所は：

1 → (0,0) 2 → (0,1) 3 → (0,2) 4 → (1,0) 5 → (1,1) 6 → (1,2) 7 → (2,0) 8 → (2,1)

現在の座標とゴールの座標の差を計算：

タイル	現在位置	目標位置	差（x）	差（y）	合計距離
1	(1,0)	(0,0)	1	0	1
2	(0,0)	(0,1)	0	1	1
3	(0,2)	(0,2)	0	0	0
4	(1,2)	(1,0)	0	2	2
5	(2,2)	(1,1)	1	1	2
6	(1,1)	(1,2)	0	1	1
7	(2,0)	(2,0)	0	0	0
8	(0,1)	(2,1)	2	0	2

※ 空白（null）は無視

合計マンハッタン距離

1 + 1 + 0 + 2 + 2 + 1 + 0 + 2 = 9

これをどう使うの？

A*では、すべての候補状態にこの「マンハッタン距離」を使って見込みの良さを評価します。

見込みが良い（距離が小さい）状態を優先的に探す
実際に使った手数 g(n) と、残りの予想手数 h(n)（=マンハッタン距離）を足した値で判断

f(n) = g(n) + h(n)

なぜこの方法が良いの？

無駄な手をあまり試さず、最短ルートを素早く見つけてくれる
ただし「最短の手数で解ける」という保証もある（安全）

まとめ

マンハッタン距離は、パズルにおける「あとどれだけ動かせば完成か？」をざっくり見積もる方法
A*アルゴリズムは、それを使って頭のよい順番で試行してくれる
今回の自動解答はこのアルゴリズムを使って「確実に・速く」解いてくれている

ソースについて

function solvePuzzle(initialTiles) {
  // ゴール状態（完成形の並び）を定義
  const goal = [...Array(8).keys()].map(n => n + 1).concat(null);

  // 空白マスの移動可能方向（右、左、下、上）
  const directions = [1, -1, 3, -3];

  // 指定された状態から移動可能な「次の状態」たちを返す関数
  function getNeighbors(state) {
    const neighbors = [];
    const empty = state.indexOf(null); // 空白マスの位置を取得

    for (const d of directions) {
      const target = empty + d;

      // 移動先が無効な場合はスキップ（境界チェック）
      if (
        target < 0 || target >= 9 ||
        (d === 1 && Math.floor(empty / 3) !== Math.floor(target / 3)) || // 行をまたぐ右移動は無効
        (d === -1 && Math.floor(empty / 3) !== Math.floor(target / 3))   // 行をまたぐ左移動は無効
      ) continue;

      // 新しい状態を作成（状態は配列で管理）
      const newState = state.slice();
      [newState[empty], newState[target]] = [newState[target], newState[empty]];

      // 次の状態と「どのタイルを動かしたか」を記録
      neighbors.push({ state: newState, move: state[target] });
    }

    return neighbors;
  }

  // マンハッタン距離を計算する関数（ヒューリスティック）
  function manhattan(state) {
    let dist = 0;
    for (let i = 0; i < 9; i++) {
      const val = state[i];
      if (val === null) continue; // 空白マスは無視

      const goalIndex = val - 1; // 正しい位置のインデックス
      // x, y の差を計算（マンハッタン距離）
      dist += Math.abs(i % 3 - goalIndex % 3) + Math.abs(Math.floor(i / 3) - Math.floor(goalIndex / 3));
    }
    return dist;
  }

  // 探索用のオープンリスト（候補状態のリスト）
  const open = [{
    state: initialTiles, // 現在の状態
    path: [],            // ここまでの移動履歴（タイル番号の配列）
    cost: 0              // 今までの移動手数
  }];

  // 探索済みの状態を記録する Set（重複探索防止）
  const visited = new Set();

  // 探索ループ（open に候補が残っている限り繰り返す）
  while (open.length > 0) {
    // f(n) = g(n) + h(n) の値が小さい順に並べる
    open.sort((a, b) => (a.cost + manhattan(a.state)) - (b.cost + manhattan(b.state)));

    // 最も良さそうな状態を取り出す
    const current = open.shift();
    const key = current.state.join(','); // 状態を文字列化（Set用）

    if (visited.has(key)) continue; // 同じ状態はスキップ
    visited.add(key);               // 新しい状態を記録

    // ゴールに到達したら、その path（解法）を返す
    if (key === goal.join(',')) return current.path;

    // 隣接する状態をすべて計算し、open に追加
    for (const neighbor of getNeighbors(current.state)) {
      open.push({
        state: neighbor.state,                         // 次の状態
        path: [...current.path, neighbor.move],        // 解法パスに move を追加
        cost: current.cost + 1                         // 移動手数を 1 加算
      });
    }
  }

  // ゴールにたどり着けなかった場合（理論上はあり得ない）空配列を返す
  return [];
}

ゲームルールの守り方について

A*アルゴリズムがスライドパズルをルール通りに解ける理由

A*とは「道を探す」だけのアルゴリズム

A*アルゴリズム自体は、特定の問題に特化していない汎用的な「最短経路探索手法」です。

つまり A* は、

地図の上で最短ルートを探す
迷路でゴールにたどり着く
数字パズルを解く

といった さまざまな問題に使える のですが、

その対象の「ルール（ゲームの仕様）」は 開発者が用意してやる必要があります。

スライドパズルでの「ルール」は何か？

プレイヤーができる操作

空白マス（null）に隣接した数字だけを動かせる
上・下・左・右の 1 マスだけ動かせる
斜め移動や2マス以上のジャンプはできない
同じ行でないと横には動かせない

これらを 「合法手（valid move）」と呼びます。

コアとなる処理：合法手だけを生成する

A*アルゴリズムが「次に試すべき状態」を決める際、
すべての移動方向を試すのではなく、「合法な動き」だけを検証対象にします。

その実装が以下の部分です：

// 空白マスの移動可能方向（右、左、下、上）
const directions = [1, -1, 3, -3];

略

// 移動先が無効な場合はスキップ（境界チェック）
if (
  target < 0 || target >= 9 ||                         // 範囲外（0〜8）のマスはダメ
  (d === 1 && Math.floor(empty / 3) !== Math.floor(target / 3)) || // 行またぎ右移動禁止
  (d === -1 && Math.floor(empty / 3) !== Math.floor(target / 3))   // 行またぎ左移動禁止
) continue;

このように、パズルのゲームルールに合わない動きは「そもそも候補にしない」 という工夫により、 A*は常にルールに従った状態のみを探索対象とします。

つまり A*は「やって良い手」しか見ていない！

A*アルゴリズムの内部では…

現在の状態から空白マスの位置を特定
上下左右に動かせる候補マスを、すべて仮に動かしてみる
ただし、ルールに違反する手は最初から除外
それぞれの状態に「良さそう度（マンハッタン距離）」をつけて記録

このループを繰り返すことで、
絶対にパズルのルールを破らずに、解ける道だけを進んでいくのです。

まとめ

A*は「道を探すプロ」だけど「どこを通っていいか」は知らない
開発者が「合法手だけを作る」ようにしてあげることで、ゲームのルールを守った探索が実現できる
今回の実装では getNeighbors() 関数の中に、スライドパズルのルールを厳密に反映した条件分岐があり、それが A* にルールを守らせる仕組みの肝になっている

３＊３の盤面と配列での扱いについて

スライドパズルを1次元配列で扱う構造と「行をまたぐ左右移動」の排除方法

パズルの盤面は3×3だが、実装は1次元配列（9要素）

スライドパズルは、盤面上では次のような3×3の配置です

0  1  2  
3  4  5  
6  7  8

ですが、JavaScriptの実装ではこれを1次元配列として扱っています

tiles = [1, 2, 3, 4, 5, 6, 7, 8, null];

インデックスから「行」と「列」を計算する方法

任意のインデックス i に対して

行（row） = Math.floor(i / 3)
列（col） = i % 3

例：

i = 5 → 行1（2行目）, 列2（右端）
i = 7 → 行2（3行目）, 列1（中央）

→カレンダーとかも同じ考え方になります。
　ある単位の長さごとに折り返す、という場合、
　座標の求め方は簡単に考えられる、という感じです。
　或いは、座標は配列に置き換えられる、とも言えます。

上下左右の移動は「インデックスの加減算」で表現

移動方向とインデックスの変化は次の通りです

右 → ＋1
左 → −1
下 → ＋3
上 → −3

「右／左移動」で行をまたいではいけない理由

例えばインデックス 2（右端）から +1 → 3 に進むと、
それは 1行目 → 2行目への行をまたぐ移動になります。
これは実際のパズルでは不正です。（隣接していないため）
一方、縦の移動は、盤外へ行かない限り合法手になります。

それを防ぐのがこの条件判定

if (
  d === 1 && Math.floor(empty / 3) !== Math.floor(target / 3)
) continue;

if (
  d === -1 && Math.floor(empty / 3) !== Math.floor(target / 3)
) continue;

これにより、「左右の移動先が同じ行に属していない」場合はスキップされます。

なぜこれで「合法手」だけになるのか？

「空白マスの現在の行」と「移動先タイルの行」が異なる場合、
それは上下方向以外の移動では 不正（行またぎ） になる。

このロジックにより、左右移動に関して

同じ行 → 有効（合法手）
行をまたいでいる → 無効（違法手）

まとめ

３＊３パズルは配列インデックスで 0〜8 の1次元として扱える
行や列の位置関係は Math.floor(i / 3), i % 3 で求められる
A* アルゴリズムでは、次に試す状態を作る時、
「この動きがルール上有効か？」を厳密にチェックしてあげれば、
それにより「ゲームのルールを破らず探索を進められる」ようになっている

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

スライドパズルをJavaScriptで自動解答させてみた

自分でパズル作ったけど、解けない( ﾟДﾟ)ってなったのでAIに解いてもらった

機能追加の背景

デモ

ソース

前回記事

自動解答機能の処理説明（autoSolve）

autoSolve() の概要

主な流れ

使用される主な関数と役割

solvePuzzle(initialTiles)

moveTile(num) ＃既存

showResult() ＃既存

フラグ制御

isAiSolving

利用タイミング

まとめ

A*アルゴリズム（スライドパズル用）とは？

基本の考え方

スライドパズルでの適用

ステート（状態）

移動操作

ゴール状態

ヒューリスティック関数 h(n) の設計

マンハッタン距離とは？

探索の流れ（簡略版）

スライドパズルにおける利点

注意点

まとめ

スライドパズルにおける A* アルゴリズムとマンハッタン距離

そもそも「A*（エースター）」って？

今回のパズルの完成形

たとえば、こんな初期状態だとします：

マンハッタン距離とは？

実際に数えてみよう！

現在の並び：

現在の座標とゴールの座標の差を計算：

合計マンハッタン距離

これをどう使うの？

なぜこの方法が良いの？

まとめ

A*アルゴリズムがスライドパズルをルール通りに解ける理由

A*とは「道を探す」だけのアルゴリズム

スライドパズルでの「ルール」は何か？

プレイヤーができる操作

コアとなる処理：合法手だけを生成する

つまり A*は「やって良い手」しか見ていない！

まとめ

スライドパズルを1次元配列で扱う構造と「行をまたぐ左右移動」の排除方法

パズルの盤面は3×3だが、実装は1次元配列（9要素）

インデックスから「行」と「列」を計算する方法

上下左右の移動は「インデックスの加減算」で表現

「右／左移動」で行をまたいではいけない理由

それを防ぐのがこの条件判定

なぜこれで「合法手」だけになるのか？

まとめ

moveTile(num)　＃既存

showResult()　＃既存

ヒューリスティック関数 `h(n)` の設計