0.はじめに
SIGNATEで「日本取引所グループ ファンダメンタルズ分析チャレンジ」というコンペが開催されています。私も参加しますが、その中で出てくる知識に関して基礎部分をまとめよう!という動機で今回は記事を書くことにしました。
今回のコンペの評価方法で「スピアマンの相関係数」というものが出てきますので、第1回は「相関係数」に関して簡単におさらいしていこうと考えています。
1.まず「相関関係」とは?
ある2つのデータ(例えばX,Y)あった時、一方が増加したときに他方が増加or減少する傾向がある2つの数字の関係のことを「相関関係がある」という。
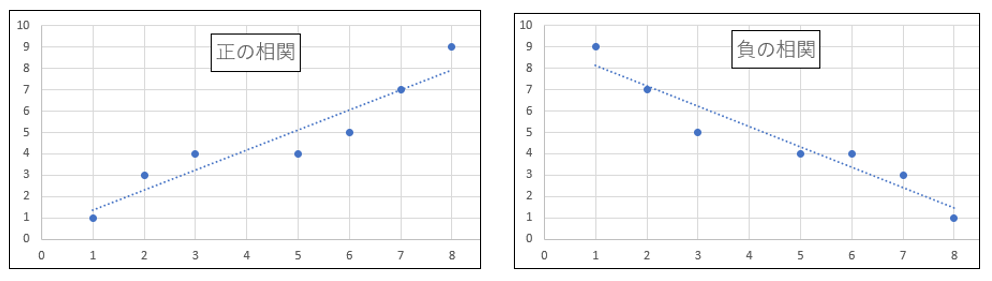
・一方の値が大きくなると、他方の値も大きくなることを「正の相関」と呼び
・一方の値が大きくなると、他方の値が小さくなることを「負の相関」と呼ぶ
・2つの値に明白な関係がみられなければ「無相関」と呼ぶ
ただし、因果関係とは違うので注意。
※因果関係とは「Xが原因でYが変化する」ことを指す。
※因果関係が認められるデータに関しては「相関関係もある」といえる
2.ピアソンの相関係数とは?
2-1.基本情報
正式名称は「ピアソンの積率相関係数」と呼ばれる。
世間一般的に「相関がある」といわれるケースは、このピアソンの相関係数を指すことが多数である。
まず「相関係数」とは、イメージとして**2つのデータの関係に何か関係がありそうだけど「どれくらい関係性が強いか?」**を数字で表す時に使用する指標のこと。
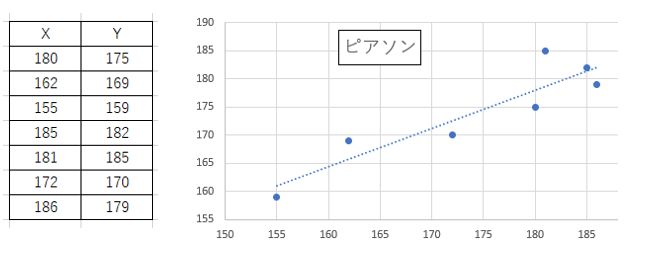
例として親の身長をX、子供の身長をYとしたときに以下のように表とピアソンの相関図が書ける。
参考として数式で示すと・・・
n組のデータ$(x_1,y_1),(x_2,y_2),・・・(x_i,y_i)$があり、それぞれの平均を$\overline{x},\overline{y}$とする。
そして$x,y$の標準偏差を$s_x,s_y$とし、$x,y$の共分散を$s_{xy}$としたときに、ピアソンの席率相関係数$r_{xy}$は次のような数式で表される
※共分散とは?:x,yの偏差の積の平均値のこと
参考:共分散とは
r_{xy} = \frac{{\displaystyle \sum_{i = 1}^n (x_i - \overline{x})
(y_i - \overline{y})}}{\sqrt{{\displaystyle \sum_{i = 1}^n
(x_i - \overline{x})^2}} \sqrt{{\displaystyle \sum_{i = 1}^n
(y_i - \overline{y})^2}}} = \frac{s_{xy}}{s_xs_y}
$r_{xy}$が1に近ければ「強い正の相関がある」と言われ、-1に近ければ「強い負の相関がある」と言われる。
※相関係数の範囲は「-1~1」の範囲である
2-2.ピアソンの相関係数を使う際の前提条件
ピアソンの相関関係に関してはどんなデータにでも使用できるわけではない。
「データが正規分布に沿ったデータである」ことが前提になっていることが注意点である。
※とある分布に沿うデータのことをパラメトリックと呼ぶので、ピアソンの相関係数はパラメトリックが前提と書いてある説明もある。
3.スピアマンの相関係数とは?
3-1.基本情報
正式名称は「スピアマンの順位相関係数」と呼ばれる。
名前の通り「順位データから求められる相関の指標」のことである。
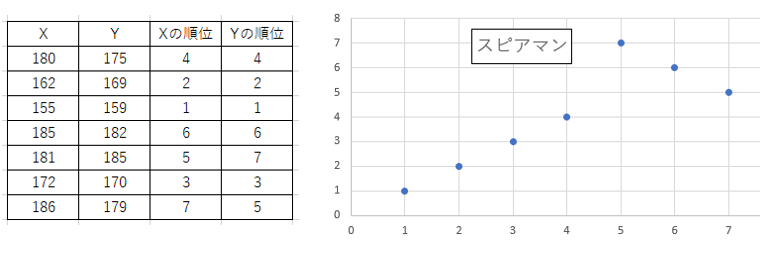
先程の例と同様に親の身長をX、子供の身長をYとしたときに、以下のように順位表とスピアマンの相関図が書ける。
参考として数式で示すと・・・
n組のデータ$(x_1,y_1),(x_2,y_2),・・・(x_i,y_i)$があった時に、それぞれの各変量に「順位」をつける。
n組のデータの中のとある$i$番目のデータ$x_i$,$y_i$の「順位の差」を$d_i$としたときに、以下式でスピアマンの順位相関係数$r_s$が計算できる
r_s = 1 - \frac{6\displaystyle \sum_{i = 1}^n {d_i}^2}{n(n^2 - 1)}
2つのデータの順序がすべて一致する場合は$r_s$が1、すべて逆順の場合は$r_s$が-1になる。
3-2.スピアマンの相関係数を使う際の前提条件
スピアマンの場合は前提条件がない。これがピアソンとの最大の違いである。
ピアソンが「パラメトリック(正規分布)」のみ対象なのに対して、スピアマンは「ノンパラメトリック(特定の分布でないもの)」でも使用可能なのが強み。
スピアマンはもちろん「パラメトリック」に関しても使用できる。
3-3.スピアマンのデメリットとメリット
スピアマンがどんな分布にも使えるなら、スピアマン一択じゃないか!!と思われるかもだが、スピアマンにも欠点がある。それは生データではなく順位データなので、それぞれの変数間の情報が削られてしまうことである。
つまり各データが「どれくらい離れているのか?」に関しての変化量情報が失われてしまう。
逆にメリットもある。
ただピアソンの相関係数は「外れ値」に弱く、1つでもデータがかけ離れたプロットがある場合にはその外れ値を取り除くかないと、相関係数がその外れ値に引っ張られて高く出てしまう場合がある。
そんな時に、このスピアマンの相関係数を使用すると「順位」で判断する為に単純に外れ値に強い
4.さいごに
今回はSIGNATEで株価コンペが始まったのをきっかけに、評価として使われる相関係数をおさらいした。そして、余談だが投資のテクニカル分析にも「RCI(Rank Correlation Index)」という指標があり、これがまさにスピアマンの順位相関係数を指している。
●RCIとは?
計算期間中に日付の経過の度に価格が毎日上昇していれば100%、逆に日付の経過の度に価格が毎日下落していれば-100%となります。
価格の幅が考慮に入れられていませんので急激な変動に対しての感応度は低いですが、相場の過熱感と共にトレンドの有無に関しても把握することができる指標
意外と身近な指標として、相関係数を使う機会も多いと思うのでこれを機に色々復習するのも大事ですね。
また。コンペには様々な知識が使われていることがチュートリアルからも確認できるので、それぞれの基礎を次回以降もまとめていければと考えています。