0.はじめに
今週は記事にするネタが思い浮かばなかったので、株関連の記事。
今回はトヨタ自動車とTOPIXのβ値をpythonで算出する方法を2種類記載します。
1.ベータ値って・・何?
β値とは、株の個別銘柄が指数にどれだけ感応度があるかっていうのを調べる指標で、株式市場(指数)が1%変化したときに、任意の株式のリターンが何%変化するかを表す係数。
それはすなわち**「リスク」を測る指標**と言える。
つまり、βが1を超える株式はより指数に比べて動く銘柄となるのでリスクが高くなる。
2.準備
今回はトヨタ自動車(7203.T)とTOPIXの比較を行い、期間は2020/1/1~2020/12/31までとする。
そして今回の株価取得は簡単の為pandas_datareader + stooq経由で行う
※本記事はβ値の算出の解説なので、株価取得部分は解説しない
※stooqは指数はあってるが、下記トヨタ含め株価データが微妙に間違っていることがあるので注意
import numpy as np
import pandas as pd
import datetime
from pandas_datareader import data as wb
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn import linear_model
# Topixとトヨタをstooqからデータフレームとして取得
start = datetime.date(2020,1,1)
end = datetime.date(2020,12,31)
tickers = ['^TPX','7203.JP'] #TOPIXとトヨタ ※stooq経由でのトヨタの株価は微妙におかしい
data = pd.DataFrame()
for t in tickers:
#終値だけ取得
data[t] = wb.DataReader(t, data_source='stooq', start=start, end=end)['Close']
data = data.iloc[::-1] #順番並び替え
data.head(2) #2行表示
| Date | ^TPX | 7203.JP |
|---|---|---|
| 2020-01-06 | 1697.49 | 7435.85 |
| 2020-01-07 | 1725.05 | 7583.29 |
3.対数利益率の計算
前日比どれくらい上昇しているか?を対数利益率で計算する
log_returns = np.log(data/data.shift(1)) #shift(1)で1日データシフトさせている
log_returns = log_returns.dropna() #1/6は前日がないのでNaN。よって取り除く
log_returns.head(2) #2行表示
| Date | ^TPX | 7203.JP |
|---|---|---|
| 2020-01-07 | 0.016105 | 0.019634 |
| 2020-01-08 | -0.013805 | -0.012784 |
4.散布図をplotしてベータ値を算出
# 共分散plot
X = log_returns.iloc[:,0] #topix
Y = log_returns.iloc[:,1] #toyota
from sklearn import linear_model
clf = linear_model.LinearRegression() #線形モデル
X2 = [[x] for x in X]
clf.fit(X2, Y) # 予測モデルを作成
print("ベータ値(回帰係数,傾き)= ", clf.coef_)
print("切片= ", clf.intercept_)
print("決定係数= ", clf.score(X2, Y))
# 散布図
plt.scatter(X2, Y)
# 回帰直線
plt.title('Linear regression')
plt.plot(X2, clf.predict(X2))
plt.xlabel(log_returns.columns[0])
plt.ylabel(log_returns.columns[1])
plt.grid()
plt.show()
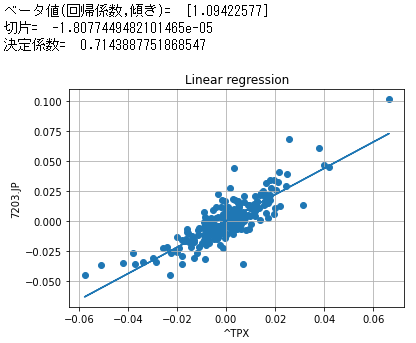
これでベータ値の算出が出来た。ベータ値とは回帰直線の傾きそのものであり、1.09となっているので市場が1%上がるとトヨタは1.09%上昇するということになる
5.線形回帰を使わない方法
ベータ値は共分散を求めることで算出でき、こちらの方が記述が短く済む。
参考:共分散とは
cov_matrix = log_returns.cov() #covは共分散を計算
cov_matrix
| Date | ^TPX | 7203.JP |
|---|---|---|
| ^TPX | 0.000204 | 0.000223 |
| 7203.JP | 0.000223 | 0.000342 |
共分散(マーケット・個別):右上、左下
分散(マーケット):左上
"""ベータ値 = 共分散(マーケット・個別)/分散(マーケット)"""
toyota_beta = cov_matrix.iloc[0,1] / cov_matrix.iloc[0,0]
print(toyota_beta)
1.0942257680186884 ※線形回帰の傾きと同じ
6.おわりに
今回はベータ値をpythonで算出した。
高ベータ値の銘柄は市場が上昇基調にあるときはより大きく上昇する一方、逆に市場が下落基調に転じるというリスクもある。よってこれを活用して例えば上げ相場は高β、下げ相場は低βにするなどして銘柄選択に役立ててみては如何だろうか?