GAN
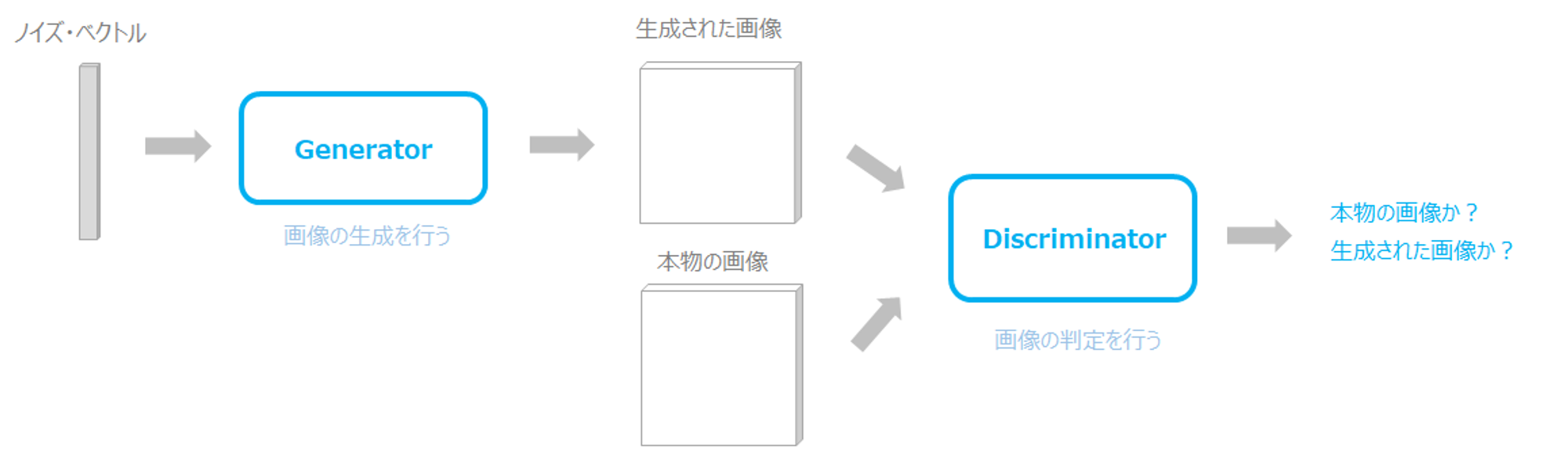
- GAN(Generative Adversarial Networks)とは、深層学習の一種で、画像、音声などのデータを生成することができるモデルです
- GANは、Generator, Discriminatorと呼ばれる2つのニューラルネットワークを使用して画像を生成します
Generator
- ランダムなノイズベクトルから画像を生成するためのニューラルネットワーク
- 学習によって画像を生成するための最適なパラメータを学習します
Discriminator
- 本物の画像とGeneratorによって生成された画像を区別するためのニューラルネットワークです
- 学習によって本物の画像とGeneratorによって生成された画像を区別するための最適なパラメータを学習します
GeneratorはDiscriminatorを騙そうと、より訓練データに近い画像を生成できるように学習し、DiscriminatorはGeneratorに騙されないように、より真贋を見分けられるように学習し、互いに学習を進めると最終的にはGeneratorが訓練データで用意した現実に存在するような画像を生成できるようになる技術がGAN
DCGAN (Deep Convolution GAN)
概要
DCGANは、GANの派生モデルの1つ
特徴
- プーリング層を使わず、代わりにストライドを利用した畳み込みを行う
- プーリング層を使用すると、画像内の細かな特徴が失われる可能性がある
- Generator、Discriminatorの両方にバッチノーマライゼーションを使用する
- 全結合層を使わない
- Generatorの活性化関数にReLUを使用する。ただし、最後のアウトプット層はTanhを使用する
- Discriminatorの活性化関数にLeakyReLUを使用する
バッチノーマライゼーションとは
1ミニバッチ内の全データの同一チャネルを平均0,分散1に正規化する処理
各層の活性化関数の出力は、適度な分散をもっていると勾配消失などの問題が起こりにくいことが知られており、各層の出力を適度に分散させるために導入された
これにより、層を深くしても学習が適切にできるようになった
また、過学習を抑制する効果もあるとされている
Generatorの実装
Generator class
class Generator(nn.Module):
# ネットワークの構造を定義
# z_dim : Generatorに入力される乱数の次元数を表すパラメータ
# image_size : 生成される画像のサイズ (64x64ピクセル)
def __init__(self, z_dim=20, image_size=64):
super(Generator, self).__init__()
# Layer 1
self.layer1 = nn.Sequential(
# 転置畳み込みを行う
nn.ConvTranspose2d(z_dim, image_size * 8,
kernel_size=4, stride=1),
# バッチノーマライゼーション
nn.BatchNorm2d(image_size * 8),
# 活性化関数 (出力層以外ReLU)
nn.ReLU(inplace=True))
# Layer 2
self.layer2 = nn.Sequential(
nn.ConvTranspose2d(image_size * 8, image_size * 4,
kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(image_size * 4),
nn.ReLU(inplace=True))
# Layer 3
self.layer3 = nn.Sequential(
nn.ConvTranspose2d(image_size * 4, image_size * 2,
kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(image_size * 2),
nn.ReLU(inplace=True))
# Layer 4
self.layer4 = nn.Sequential(
nn.ConvTranspose2d(image_size * 2, image_size,
kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(image_size),
nn.ReLU(inplace=True))
# Last Layer
self.last = nn.Sequential(
nn.ConvTranspose2d(image_size, 1, kernel_size=4,
stride=2, padding=1),
# 活性化関数 (出力層のみTanh)
# 生成された画像のピクセル値を-1から1の範囲に正規化
nn.Tanh())
# 注意:白黒画像なので出力チャネルは1つだけ
# 順伝播を定義
def forward(self, z):
out = self.layer1(z)
out = self.layer2(out)
out = self.layer3(out)
out = self.layer4(out)
out = self.last(out)
return out
-
layer1~4
転置畳み込み → バッチノーマライゼーション → ReLU
-
last
転置畳み込み → Tanh
各層の入力と出力 (z_dim=20, image_size=64 のとき)
4次元のテンソル
- Layer 1
- 入力サイズ: (1, 20, 1, 1) (バッチサイズ, z_dim, 1, 1)
- 出力サイズ: (1, 512, 4, 4)
- Layer 2
- 入力サイズ: (1, 512, 4, 4)
- 出力サイズ: (1, 256, 8, 8)
- Layer 3
- 入力サイズ: (1, 256, 8, 8)
- 出力サイズ: (1, 128, 16, 16)
- Layer 4
- 入力サイズ: (1, 128, 16, 16)
- 出力サイズ: (1, 64, 32, 32)
- Last Layer
- 入力サイズ: (1, 64, 32, 32)
- 出力サイズ: (1, 1, 64, 64) (バッチサイズ, 1, image_size, image_size)
動作
import matplotlib.pyplot as plt
%matplotlib inline
# Generatorクラスのインスタンスを作成
G = Generator(z_dim=20, image_size=64)
# 入力する乱数
input_z = torch.randn(1, 20)
# テンソルサイズを(1, 20, 1, 1)に変形
input_z = input_z.view(input_z.size(0), input_z.size(1), 1, 1)
# 偽画像を出力
fake_images = G(input_z)
img_transformed = fake_images[0][0].detach().numpy()
plt.imshow(img_transformed, 'gray')
plt.show()
ランダムなベクトルを入力として受け取り、そのベクトルから画像を生成します。
Discriminatorの実装
Discriminator class
class Discriminator(nn.Module):
def __init__(self, z_dim=20, image_size=64):
super(Discriminator, self).__init__()
# Layer 1
self.layer1 = nn.Sequential(
# 畳み込み層
nn.Conv2d(1, image_size, kernel_size=4,
stride=2, padding=1),
# 活性化関数
nn.LeakyReLU(0.1, inplace=True))
# 注意:白黒画像なので入力チャネルは1つだけ
# Layer 2
self.layer2 = nn.Sequential(
nn.Conv2d(image_size, image_size*2, kernel_size=4,
stride=2, padding=1),
nn.LeakyReLU(0.1, inplace=True))
# Layer 3
self.layer3 = nn.Sequential(
nn.Conv2d(image_size*2, image_size*4, kernel_size=4,
stride=2, padding=1),
nn.LeakyReLU(0.1, inplace=True))
# Layer 4
self.layer4 = nn.Sequential(
nn.Conv2d(image_size*4, image_size*8, kernel_size=4,
stride=2, padding=1),
nn.LeakyReLU(0.1, inplace=True))
# Last Layer
# 畳み込み層のみ
self.last = nn.Conv2d(image_size*8, 1, kernel_size=4, stride=1)
def forward(self, x):
out = self.layer1(x)
out = self.layer2(out)
out = self.layer3(out)
out = self.layer4(out)
out = self.last(out)
return out
畳み込み → LeakyReLU
全結合層を使わず畳み込み層のみで、1×1のアウトプットにします。
LeakyReLU
入力された値が負の値であった場合に、0ではなく「入力された値×係数」を出力
https://vidyasheela.com/post/leaky-relu-activation-function-with-python-code#google_vignette
各層の入力と出力 (z_dim=20, image_size=64 のとき)
4次元のテンソル
- Layer1
- 入力サイズ: (1, 1, 64, 64)
- 出力サイズ: (1, 64, 32, 32)
- Layer 2
- 入力サイズ: (1, 64, 32, 32)
- 出力サイズ: (1, 128, 16, 16)
- Layer 3
- 入力サイズ: (1, 128, 16, 16)
- 出力サイズ: (1, 256, 8, 8)
- Layer 4
- 入力サイズ: (1, 256, 8, 8)
- 出力サイズ: (1, 512, 4, 4)
- Last Layer
- 入力サイズ: (1, 512, 4, 4)
- 出力サイズ: (1, 1, 1, 1)
入力画像が教師データか、生成された画像化を判定した値に対応
動作
# 動作確認
# Generatorで偽画像を生成し、それをDiscriminatorに入力して判断させる
D = Discriminator(z_dim=20, image_size=64)
# 偽画像を生成
input_z = torch.randn(1, 20)
input_z = input_z.view(input_z.size(0), input_z.size(1), 1, 1)
fake_images = G(input_z)
# 偽画像をDに入力
d_out = D(fake_images)
# クラス分類を出力させたいので、出力d_outにSigmoidをかけて0から1に変換
# 偽画像ならラベル0、教師データならラベル1
print(nn.Sigmoid()(d_out))
# 出力結果
tensor([[[[0.5014]]]], grad_fn=<SigmoidBackward0>)
まだDiscriminatorの学習をしていないので、判断がつかず中間の0.5当たりの値が出力された
損失関数
Generatorの損失関数
GeneratorはDiscriminatorを騙したいので、Generatorが生成した画像に対して、Dの判定が失敗方向になればいい
つまり、Discriminatorの損失関数を最大化すればよいので
$$
\sum_{i=1}^{M}
[l_i log y_i + (1-l_i) log(1-y_i)]
$$
が損失関数となるが、ここで
- ラベル $l_i$ は偽画像のとき0である
- $y = D(x)$であり、Generatorは入力$z_i$から画像を生成する
ことから、Generatorのミニバッチでの損失関数は
$$
\sum_{i=1}^{M}
log(1-D(G(z_i)))
$$
となり、この式で計算される損失の値をできるだけ小さくすれば、より騙せる画像を生成できる。
しかし、初期のGeneratorが生成する画像は教師データとの違いが大きく、学習があまり進んでいない段階でDiscriminatorに判定されてしまう。
すると、上式の$D(G(z_i))$が非常に小さくなり、Generatorの損失がほぼ0になってしまう。つまりGeneratorの学習が進まない。
そこで、$D(G(z_i))$が1と判定されれば良いと考え、DCGANではGeneratorの損失関数を
$$
-\sum_{i=1}^{M}
logD(G(z_i))
$$
としている。
(Generatorがうまく騙すと値は0となり、見抜かれると正の大きな値となる。)
つまり、元の式では見抜かれても損失値が0で学習が進まないが、改良した式では見抜かれると大きな損失値となり学習が進む。
Discriminatorの損失関数
分類を間違えると損失が大きくなるようにする
シグモイド → バイナリクロスエントロピー
x : 入力される画像データ
y : Discriminatorの出力 y = D(x) (0 ≤ y ≤ 1)
l : 正しいラベル (l ∈ {0, 1})(偽データはラベル0、教師データはラベル1)
Discriminatorの出力が正しいかどうかは
$$
y^l (1-y)^{1-l}
$$
で表される。
(正解ラベル l と予測出力 y の値が同じなら1、異なる間違った予測なら0になる。)
この判定がミニバッチのデータ数M個分あるので、その同時確率は
$$
\prod_{i=1}^{M}
y_i^{l_i}
(1-y_i)^{1-l_i}
$$
となり、対数をとると
$$
\sum_{i=1}^{M}
[l_i log y_i + (1-l_i) log(1-y_i)]
$$
となる。
最小化のほうが実装時に考えやすいので、マイナスをかけると
$$
-\sum_{i=1}^{M}
[l_i log y_i + (1-l_i) log(1-y_i)]
$$
これがDiscriminatorのニューラルネットワークの損失関数
実装のイメージ
# Discriminatorの誤差関数の実装のイメージ
# maximize log(D(x)) + log(1 - D(G(z)))
# ※ xが未定義なので動作はエラーになります
# ---------------
# 正解ラベルを作成
mini_batch_size = 2
label_real = torch.full((mini_batch_size,), 1)
# 偽ラベルを作成
label_fake = torch.full((mini_batch_size,), 0)
# 誤差関数を定義
# Binary Cross Entropy
criterion = nn.BCEWithLogitsLoss(reduction='mean')
# 真の画像を判定
d_out_real = D(x)
# 偽の画像を生成して判定
input_z = torch.randn(mini_batch_size, 20)
input_z = input_z.view(input_z.size(0), input_z.size(1), 1, 1)
fake_images = G(input_z)
d_out_fake = D(fake_images)
# 誤差を計算
d_loss_real = criterion(d_out_real.view(-1), label_real)
d_loss_fake = criterion(d_out_fake.view(-1), label_fake)
d_loss = d_loss_real + d_loss_fake
Dataset・DataLoaderの作成
教師データとなる手書き数字の画像を格納したDataLoaderを作成する。
これまでの章と基本的に同じだが、学習と検証などにDatasetを分けずに作成する。
- 実装例
-
学習、検証の画像データとアノテーションデータへのファイルパスリスト
def make_datapath_list(): """学習、検証の画像データとアノテーションデータへのファイルパスリストを作成する。 """ train_img_list = list() # 画像ファイルパスを格納 for img_idx in range(200): img_path = "./data/img_78/img_7_" + str(img_idx)+'.jpg' train_img_list.append(img_path) img_path = "./data/img_78/img_8_" + str(img_idx)+'.jpg' train_img_list.append(img_path) # 生成された画像ファイルのパスリスト return train_img_list -
画像の前処理クラス
# 画像の前処理クラス class ImageTransform(): """ 画像の正規化を行うための変換操作を定義 mean : 画像のチャネルごとの平均値 std : 画像のチャンネルごとの標準偏差 """ def __init__(self, mean, std): self.data_transform = transforms.Compose([ # 画像をテンソルに変換 transforms.ToTensor(), # 指定された平均値と標準偏差を使用してテンソルの値を正規化 transforms.Normalize(mean, std) ]) """ 実際に画像の前処理を行うための関数 """ def __call__(self, img): return self.data_transform(img) -
画像のDatasetクラス
# 画像のDatasetクラス。PyTorchのDatasetクラスを継承 class GAN_Img_Dataset(data.Dataset): """ 引数を受け取り、それぞれをインスタンス変数として保持 file_list : データセットの画像ファイルのリスト transform : 画像の前処理を行うためのオブジェクト """ def __init__(self, file_list, transform): self.file_list = file_list self.transform = transform """ 画像の枚数を返す """ def __len__(self): return len(self.file_list) """ 前処理をした画像のTensor形式のデータを取得 """ def __getitem__(self, index): img_path = self.file_list[index] img = Image.open(img_path) # [高さ][幅]白黒 # 画像の前処理 img_transformed = self.transform(img) return img_transformed -
DataLoaderの作成と動作確認
# DataLoaderの作成と動作確認 # データセットからデータをミニバッチとして取得 # ファイルリストを作成 train_img_list=make_datapath_list() # Datasetを作成 mean = (0.5,) std = (0.5,) train_dataset = GAN_Img_Dataset( file_list=train_img_list, transform=ImageTransform(mean, std)) # DataLoaderを作成 batch_size = 64 train_dataloader = torch.utils.data.DataLoader( train_dataset, batch_size=batch_size, shuffle=True) # データの順序をシャッフル # 動作の確認 batch_iterator = iter(train_dataloader) # イテレータに変換 imges = next(batch_iterator) # 1番目の要素を取り出す print(imges.size())出力結果
torch.Size([64, 1, 64, 64])- ミニバッチのサイズが64
- 色チャネルが1(白黒画像)
- サイズが64x64ピクセル
であることを示している。
教師データのDataLoaderとして変数train_dataloaderが用意できた。
-
学習
-
ネットワークの初期化
# ネットワークの重みを初期化するための関数 def weights_init(m): classname = m.__class__.__name__ if classname.find('Conv') != -1: # 畳み込み層と転置畳み込み層の重みを初期化 nn.init.normal_(m.weight.data, 0.0, 0.02) nn.init.constant_(m.bias.data, 0) elif classname.find('BatchNorm') != -1: # バッチノーマライゼーション層の重みを初期化 nn.init.normal_(m.weight.data, 1.0, 0.02) nn.init.constant_(m.bias.data, 0) # 初期化の実施 G.apply(weights_init) D.apply(weights_init) print("ネットワークの初期化完了") -
モデルを学習させる関数を作成
# モデルを学習させる関数を作成 def train_model(G, D, dataloader, num_epochs): """ 以下を省略 1. 使用するデバイスの確認、最適化手法や誤差関数の設定 2. モデルを訓練モードに設定、GPUへ転送 3. イテレーション回数やログの初期化など、学習に必要な変数や設定 4. エポックごとのループを開始 """ # データローダーからミニバッチごとにデータを取り出し、以下の手順を繰り返す for imges in dataloader: """ -------------------- 5. Discriminatorの学習 -------------------- 真の画像を判定し、偽の画像を生成して判定します。 誤差を計算し、バックプロパゲーションを行います。 """ # GPUが使えるならGPUにデータを送る imges = imges.to(device) # 正解ラベルと偽ラベルを作成 # epochの最後のイテレーションはミニバッチの数が少なくなる mini_batch_size = imges.size()[0] label_real = torch.full((mini_batch_size,), 1).to(device) label_fake = torch.full((mini_batch_size,), 0).to(device) # 真の画像を判定 d_out_real = D(imges) # 偽の画像を生成して判定 input_z = torch.randn(mini_batch_size, z_dim).to(device) input_z = input_z.view(input_z.size(0), input_z.size(1), 1, 1) fake_images = G(input_z) d_out_fake = D(fake_images) # 誤差を計算 d_loss_real = criterion(d_out_real.view(-1), label_real) d_loss_fake = criterion(d_out_fake.view(-1), label_fake) d_loss = d_loss_real + d_loss_fake # バックプロパゲーション g_optimizer.zero_grad() d_optimizer.zero_grad() d_loss.backward() d_optimizer.step() """ -------------------- 6. Generatorの学習 -------------------- 偽の画像を生成して判定し、誤差を計算します。 バックプロパゲーションを行います。 """ # 偽の画像を生成して判定 input_z = torch.randn(mini_batch_size, z_dim).to(device) input_z = input_z.view(input_z.size(0), input_z.size(1), 1, 1) fake_images = G(input_z) d_out_fake = D(fake_images) # 誤差を計算 g_loss = criterion(d_out_fake.view(-1), label_real) # バックプロパゲーション g_optimizer.zero_grad() d_optimizer.zero_grad() g_loss.backward() g_optimizer.step() """ -------------------- 7. 記録 -------------------- 各損失の値を記録します。 """ epoch_d_loss += d_loss.item() epoch_g_loss += g_loss.item() iteration += 1 # 各エポックの終了時に、損失の平均値や経過時間を表示 t_epoch_finish = time.time() print('-------------') print('epoch {} || Epoch_D_Loss:{:.4f} ||Epoch_G_Loss:{:.4f}'.format( epoch, epoch_d_loss/batch_size, epoch_g_loss/batch_size)) print('timer: {:.4f} sec.'.format(t_epoch_finish - t_epoch_start)) t_epoch_start = time.time() return G, D -
学習・検証を実行
# 学習・検証を実行する num_epochs = 200 G_update, D_update = train_model( G, D, dataloader=train_dataloader, num_epochs=num_epochs) -
生成画像と訓練データを可視化
# 生成画像と訓練データを可視化する device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu") # 入力の乱数生成 batch_size = 8 z_dim = 20 fixed_z = torch.randn(batch_size, z_dim) fixed_z = fixed_z.view(fixed_z.size(0), fixed_z.size(1), 1, 1) # 画像生成 G_update.eval() fake_images = G_update(fixed_z.to(device)) # 訓練データ batch_iterator = iter(train_dataloader) # イテレータに変換 imges = next(batch_iterator) # 1番目の要素を取り出す # 出力 fig = plt.figure(figsize=(15, 6)) for i in range(0, 5): # 上段に訓練データを plt.subplot(2, 5, i+1) plt.imshow(imges[i][0].cpu().detach().numpy(), 'gray') # 下段に生成データを表示する plt.subplot(2, 5, 5+i+1) plt.imshow(fake_images[i][0].cpu().detach().numpy(), 'gray')

SAGAN (Self-Attention GAN)
概要
従来のGANの問題点
転置畳み込みを繰り返すことで特徴量マップが大きくなるが、**「転置畳み込みではどうしても局所的な情報の拡大にしかならない」**という問題がある。
画像全体の大域的な特徴量を考慮したい
Self-Attention で解決
技術
Self-Attention
入力データ内の異なる位置の要素間の関連性を計算し、重要な情報を強調することで、GANの性能向上に貢献する概念
Generatorではlayer1~4とlast layerで徐々に生成画像を拡大した。
この途中のlayer間の出力をxを次のlayerにそのまま入力するのではなく、大域的な情報を考慮してxを調整した
$$
y=x+γο
$$
を入力することを考える。
γ : 適当な係数
ο : xを大域的な情報を用いて調整する値(Self-Attention Map)
この、大域的な情報を考慮して調整した特徴量yが次のlayerへの入力になる。
Self-Attention Mapを作成する方法
xのテンソルサイズをC×H×W(チャネル数×高さ×幅)と表す。
-
xを行列演算しやすいようにサイズをC×H×Wから、C×Nへ変形する。(N=W×H)
-
x同士の掛け算 $S=x^Tx$を作成する。(SはN×Nサイズ)
Sの要素$s_{ij}$は画像位置$i$が画像位置$j$とどのくらい似ているかを示す。 -
Sを規格化した行列βを作成する。
行方向にソフトマックス関数を計算して、各画像位置が画像位置$j$と似ている度の総和を1にしてから転置する。$$
β_{j,i}=
\frac
{\exp(s_{ij})}
{\sum_{i=1}^{N}
\exp(s_{ij})
}
$$この行列$\beta_{j,i}$は、位置$j$の特徴量が位置$i$の特徴量とどの程度似ているかを示す。
Attention Mapと呼ばれる。 -
C×Nの行列xとAttention Mapを掛け算する。
現在のxに対応し、xを大域的な情報から調整する量であるSelf-Attention Mapの$\omicron$が計算できる。$$
\omicron=x\beta^T
$$
Self-Attention が必要な理由
Q. なぜ転置畳み込みや通常の畳み込みでは局所的な情報しか取得できないのか?
A. カーネルサイズを小さく規定しているから。
カーネルサイズが小さいと小さい範囲しか参照できず、局所的な情報しか取得できない。
Q. 巨大なカーネルを用意すればいいのではないか?
A. 計算コストが大きくなり、うまく学習できない。計算コストを抑えるためにも、何らかの制限をかけて大域的な情報を考慮させる仕組みが必要。
そのような、入力データの位置情報全体に対するカーネルのような機能を持ちつつも制限を与えて計算コストを抑える手段がSelf-Attention。
Self-Attentionでは計算コストを抑える制限として、
「入力データのとあるセルに対して特徴量を計算する際に、着目すべきセルは、自分自身と値が似ているセルとする」
というものを与える。
カーネルサイズNの通常の畳み込みや転置畳み込みのケースでは、
「入力データのとあるセルに対して特徴量を計算する際に、着目すべきセルは、周囲N×Nの範囲のセルとする」
という表現に対応。
要はカーネルサイズ最大の畳み込み層だが、そのカーネルの値を学習させるのではなく、自分自身との特徴量の値が似ている度合いをカーネルの値として毎回データごとに計算する、というイメージ。
しかし、計算コストを抑えるための制限として、上の制限は強いので、入力データxに対してそのままSelf-Attentionをかけると性能が良くなりにくい。
制限があってもうまく入力データxから大域的な情報を考慮した特徴量を計算できるように、xを一度特徴量変換してからSelf-Attentionに与えるようにする。
その手法としてpointwise convolutionという層を使う。
pointwise convolution (1 × 1 Convolutions)
xをSelf-Attentionに与える前に、カーネルサイズが1×1の畳み込み層で、xをサイズC×H×WからC’×H×Wへと変換する。
この1×1の畳み込みのことをpointwise convolutionと呼ぶ。
-
カーネルサイズが1の畳み込み処理にどのような意味があるのか
p. 270, 図 5.3.3 参照
入力データのチャネルごとの線形和を作成して、その1×1の畳み込み層の出力チャネル数を変化させることで、元の入力xのチャネル数をCからC’に変化させる。
これによって入力xの次元圧縮を行うことができる。
-
なぜpointwise convolutionを使用するのか
- 制限下でもうまく機能する特徴量に入力xを変換するため。
- Self-AttentionではN×Cの行列とC×Nの行列の掛け算をするので、Cを小さくしておいて、計算コストを抑えるため。
Spectral Normalization
GANがうまく機能するには、Discriminatorがリプシッツ連続性(Lipschitz continuity)を有する必要がある。
SAGANではSpectral Normalizationという概念を使って、畳み込み層の重みの規格化を行い、リプシッツ連続性をDiscriminatorが有するようにする。
-
リプシッツ連続性とは
「Discriminatorへの入力画像がほんの少し変化しても出力は変化しない」というイメージ。
逆にリプシッツ連続性が保たれていないと、「Discriminatorへの入力画像がほんの少し変化すると出力がとても変化する」ということ。
-
Spectral Normalizationの内容
GANの学習がうまくいくように層の重みを正規化する
イメージ
とある層へ入力されるテンソルデータと、その層から出力されるテンソルを考える。入力の特定の部分が出力時に元より大きくなる場合、その成分は、その層の処理において拡大されることになる。
入力画像Aと入力画像Bがあり、AとBはほとんど同じで、少しだけ違う部分があるとして、その異なる部分に上記のような大きくなるテンソル成分を含んでいると、入力画像の小さな変化は拡大されることになる。このような状態では、これが繰り返されると出力手前ではAとBの違いは大きな違いとなっており、最終的な識別結果も大きく変わってしまう。
つまり、リプシッツ連続性が保たれていない状態になる。
それを防ぐために、層への入力テンソルのどのような成分でも出力テンソルでは拡大されることがないように、様々な成分が拡大される値のうち最大値を使用して層の重みパラメータを割り算して規格化する。
SAGANではDiscriminatorだけでなくGeneratorにも使用する。
実装
Self-Attention
class Self_Attention(nn.Module):
""" Self-AttentionのLayer"""
# 畳み込み層を初期化
def __init__(self, in_dim):
super(Self_Attention, self).__init__()
# 1×1の畳み込み層によるpointwise convolutionを用意
self.query_conv = nn.Conv2d(
in_channels=in_dim, out_channels=in_dim//8, kernel_size=1)
self.key_conv = nn.Conv2d(
in_channels=in_dim, out_channels=in_dim//8, kernel_size=1)
self.value_conv = nn.Conv2d(
in_channels=in_dim, out_channels=in_dim, kernel_size=1)
# Attention Map作成時の規格化のソフトマックス
self.softmax = nn.Softmax(dim=-2)
# 元の入力xとSelf-Attention Mapであるoを足し算するときの係数
# output = x +gamma*o
# 最初はgamma=0で、学習させていく
self.gamma = nn.Parameter(torch.zeros(1))
def forward(self, x):
"""
入力変数Xを保存
"""
X = x
"""
入力Xからクエリとキーを抽出
それぞれの出力は、(バッチサイズ, C', N)
クエリとキーのテンソルを転置し、行列積を計算
Self-Attention Mapの元となる行列Sが得られる
"""
# 畳み込みをしてから、サイズを変形する。 B,C',W,H→B,C',N へ
proj_query = self.query_conv(X).view(
X.shape[0], -1, X.shape[2]*X.shape[3]) # サイズ:B,C',N
proj_query = proj_query.permute(0, 2, 1) # 転置操作
proj_key = self.key_conv(X).view(
X.shape[0], -1, X.shape[2]*X.shape[3]) # サイズ:B,C',N
# かけ算
S = torch.bmm(proj_query, proj_key) # bmmはバッチごとの行列かけ算です
"""
行列Sを正規化するために、Softmax関数を適用
正規化されたSelf-Attention Mapを得るために、行列Sを再度転置
"""
# 規格化
# 行方向の和を1にするために次元を指定
attention_map_T = self.softmax(S) # 行i方向の和を1にするソフトマックス関数
attention_map = attention_map_T.permute(0, 2, 1) # 転置をとる
"""
入力Xから値を抽出するために、value_convを使用
出力は(バッチサイズ, C, N)
Self-Attention Mapと値の行列積を転置してから計算
"""
# Self-Attention Mapを計算する
proj_value = self.value_conv(X).view(
X.shape[0], -1, X.shape[2]*X.shape[3]) # サイズ:B,C,N
o = torch.bmm(proj_value, attention_map.permute(
0, 2, 1)) # Attention Mapは転置してかけ算
"""
Self-Attention Mapであるoのテンソルサイズを入力Xに合わせて変形
元の入力xにガンマ係数を乗じて足し合わせた結果を出力
"""
# Self-Attention MapであるoのテンソルサイズをXにそろえて、出力にする
o = o.view(X.shape[0], X.shape[1], X.shape[2], X.shape[3])
out = x+self.gamma*o
return out, attention_map
Generator
"""
変更点
1. 転置畳み込み層にSpectral Normalizationを追加
2. layer3-layer4, layer4-lastにSelf-Attention層を追加
"""
class Generator(nn.Module):
def __init__(self, z_dim=20, image_size=64):
super(Generator, self).__init__()
self.layer1 = nn.Sequential(
# Spectral Normalizationを追加
nn.utils.spectral_norm(nn.ConvTranspose2d(z_dim, image_size * 8,
kernel_size=4, stride=1)),
nn.BatchNorm2d(image_size * 8),
nn.ReLU(inplace=True))
self.layer2 = nn.Sequential(
# Spectral Normalizationを追加
nn.utils.spectral_norm(nn.ConvTranspose2d(image_size * 8, image_size * 4,
kernel_size=4, stride=2, padding=1)),
nn.BatchNorm2d(image_size * 4),
nn.ReLU(inplace=True))
self.layer3 = nn.Sequential(
# Spectral Normalizationを追加
nn.utils.spectral_norm(nn.ConvTranspose2d(image_size * 4, image_size * 2,
kernel_size=4, stride=2, padding=1)),
nn.BatchNorm2d(image_size * 2),
nn.ReLU(inplace=True))
# Self-Attention層を追加
self.self_attntion1 = Self_Attention(in_dim=image_size * 2)
self.layer4 = nn.Sequential(
# Spectral Normalizationを追加
nn.utils.spectral_norm(nn.ConvTranspose2d(image_size * 2, image_size,
kernel_size=4, stride=2, padding=1)),
nn.BatchNorm2d(image_size),
nn.ReLU(inplace=True))
# Self-Attention層を追加
self.self_attntion2 = Self_Attention(in_dim=image_size)
self.last = nn.Sequential(
nn.ConvTranspose2d(image_size, 1, kernel_size=4,
stride=2, padding=1),
nn.Tanh())
# 注意:白黒画像なので出力チャネルは1つだけ
def forward(self, z):
out = self.layer1(z)
out = self.layer2(out)
out = self.layer3(out)
out, attention_map1 = self.self_attntion1(out)
out = self.layer4(out)
out, attention_map2 = self.self_attntion2(out)
out = self.last(out)
return out, attention_map1, attention_map2
# 動作確認
import matplotlib.pyplot as plt
%matplotlib inline
G = Generator(z_dim=20, image_size=64)
# 入力する乱数
input_z = torch.randn(1, 20)
# テンソルサイズを(1, 20, 1, 1)に変形
input_z = input_z.view(input_z.size(0), input_z.size(1), 1, 1)
# 偽画像を出力
fake_images, attention_map1, attention_map2 = G(input_z)
img_transformed = fake_images[0][0].detach().numpy()
plt.imshow(img_transformed, 'gray')
plt.show()

Discriminator
"""
変更点
1. last以外の畳み込み層にSpectral Normalizationを追加
2. layer3-layer4, layer4-lastにSelf-Attention層を追加
"""
class Discriminator(nn.Module):
def __init__(self, z_dim=20, image_size=64):
super(Discriminator, self).__init__()
self.layer1 = nn.Sequential(
# Spectral Normalizationを追加
nn.utils.spectral_norm(nn.Conv2d(1, image_size, kernel_size=4,
stride=2, padding=1)),
nn.LeakyReLU(0.1, inplace=True))
# 注意:白黒画像なので入力チャネルは1つだけ
self.layer2 = nn.Sequential(
# Spectral Normalizationを追加
nn.utils.spectral_norm(nn.Conv2d(image_size, image_size*2, kernel_size=4,
stride=2, padding=1)),
nn.LeakyReLU(0.1, inplace=True))
self.layer3 = nn.Sequential(
# Spectral Normalizationを追加
nn.utils.spectral_norm(nn.Conv2d(image_size*2, image_size*4, kernel_size=4,
stride=2, padding=1)),
nn.LeakyReLU(0.1, inplace=True))
# Self-Attention層を追加
self.self_attntion1 = Self_Attention(in_dim=image_size*4)
self.layer4 = nn.Sequential(
# Spectral Normalizationを追加
nn.utils.spectral_norm(nn.Conv2d(image_size*4, image_size*8, kernel_size=4,
stride=2, padding=1)),
nn.LeakyReLU(0.1, inplace=True))
# Self-Attention層を追加
self.self_attntion2 = Self_Attention(in_dim=image_size*8)
self.last = nn.Conv2d(image_size*8, 1, kernel_size=4, stride=1)
def forward(self, x):
out = self.layer1(x)
out = self.layer2(out)
out = self.layer3(out)
out, attention_map1 = self.self_attntion1(out)
out = self.layer4(out)
out, attention_map2 = self.self_attntion2(out)
out = self.last(out)
return out, attention_map1, attention_map2
# 動作確認
D = Discriminator(z_dim=20, image_size=64)
# 偽画像を生成
input_z = torch.randn(1, 20)
input_z = input_z.view(input_z.size(0), input_z.size(1), 1, 1)
fake_images, _, _ = G(input_z)
# 偽画像をDに入力
d_out, attention_map1, attention_map2 = D(fake_images)
# 出力d_outにSigmoidをかけて0から1に変換
print(nn.Sigmoid()(d_out))
tensor([[[[0.4980]]]], grad_fn=<SigmoidBackward>)
DataLoader
基本的にDCGANと同じだが、損失関数が異なる。
-
Discriminatorの損失関数
SAGANでは損失関数を hinge version of the advarsarial loss というものに変更
$$
-\frac1M
\sum_{i=1}^{M}
[
l_i * \min(0,-1+y_i)
+
(1 - l_i) * \min(0,-1 - y_i)
]
$$ -
Generatorの損失関数
$$
-\frac1M
\sum_{i=1}^{M}
D(G(z_i))
$$hinge versionの損失関数を使用している理由は、論文著者によると通常のGANの損失関数よりも経験的にうまく学習できるからだそう。
学習
-
モデルを学習させる関数
# モデルを学習させる関数を作成 def train_model(G, D, dataloader, num_epochs): # GPUが使えるかを確認 device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu") print("使用デバイス:", device) # 最適化手法の設定 g_lr, d_lr = 0.0001, 0.0004 beta1, beta2 = 0.0, 0.9 g_optimizer = torch.optim.Adam(G.parameters(), g_lr, [beta1, beta2]) d_optimizer = torch.optim.Adam(D.parameters(), d_lr, [beta1, beta2]) # 誤差関数を定義 → hinge version of the adversarial lossに変更 # criterion = nn.BCEWithLogitsLoss(reduction='mean') # パラメータをハードコーディング z_dim = 20 mini_batch_size = 64 # ネットワークをGPUへ G.to(device) D.to(device) G.train() # モデルを訓練モードに D.train() # モデルを訓練モードに # ネットワークがある程度固定であれば、高速化させる torch.backends.cudnn.benchmark = True # 画像の枚数 num_train_imgs = len(dataloader.dataset) batch_size = dataloader.batch_size # イテレーションカウンタをセット iteration = 1 logs = [] # epochのループ for epoch in range(num_epochs): # 開始時刻を保存 t_epoch_start = time.time() epoch_g_loss = 0.0 # epochの損失和 epoch_d_loss = 0.0 # epochの損失和 print('-------------') print('Epoch {}/{}'.format(epoch, num_epochs)) print('-------------') print('(train)') # データローダーからminibatchずつ取り出すループ for imges in dataloader: # -------------------- # 1. Discriminatorの学習 # -------------------- # ミニバッチがサイズが1だと、バッチノーマライゼーションでエラーになるのでさける # issue #186より不要なのでコメントアウト # if imges.size()[0] == 1: # continue # GPUが使えるならGPUにデータを送る imges = imges.to(device) # 正解ラベルと偽ラベルを作成 # epochの最後のイテレーションはミニバッチの数が少なくなる mini_batch_size = imges.size()[0] #label_real = torch.full((mini_batch_size,), 1).to(device) #label_fake = torch.full((mini_batch_size,), 0).to(device) # 真の画像を判定 d_out_real, _, _ = D(imges) # 偽の画像を生成して判定 input_z = torch.randn(mini_batch_size, z_dim).to(device) input_z = input_z.view(input_z.size(0), input_z.size(1), 1, 1) fake_images, _, _ = G(input_z) d_out_fake, _, _ = D(fake_images) # 誤差を計算→hinge version of the adversarial lossに変更 # d_loss_real = criterion(d_out_real.view(-1), label_real) # d_loss_fake = criterion(d_out_fake.view(-1), label_fake) d_loss_real = torch.nn.ReLU()(1.0 - d_out_real).mean() # 誤差 d_out_realが1以上で誤差0になる。d_out_real>1で、 # 1.0 - d_out_realが負の場合ReLUで0にする d_loss_fake = torch.nn.ReLU()(1.0 + d_out_fake).mean() # 誤差 d_out_fakeが-1以下なら誤差0になる。d_out_fake<-1で、 # 1.0 + d_out_realが負の場合ReLUで0にする d_loss = d_loss_real + d_loss_fake # バックプロパゲーション g_optimizer.zero_grad() d_optimizer.zero_grad() d_loss.backward() d_optimizer.step() # -------------------- # 2. Generatorの学習 # -------------------- # 偽の画像を生成して判定 input_z = torch.randn(mini_batch_size, z_dim).to(device) input_z = input_z.view(input_z.size(0), input_z.size(1), 1, 1) fake_images, _, _ = G(input_z) d_out_fake, _, _ = D(fake_images) # 誤差を計算→hinge version of the adversarial lossに変更 #g_loss = criterion(d_out_fake.view(-1), label_real) g_loss = - d_out_fake.mean() # バックプロパゲーション g_optimizer.zero_grad() d_optimizer.zero_grad() g_loss.backward() g_optimizer.step() # -------------------- # 3. 記録 # -------------------- epoch_d_loss += d_loss.item() epoch_g_loss += g_loss.item() iteration += 1 # epochのphaseごとのlossと正解率 t_epoch_finish = time.time() print('-------------') print('epoch {} || Epoch_D_Loss:{:.4f} ||Epoch_G_Loss:{:.4f}'.format( epoch, epoch_d_loss/batch_size, epoch_g_loss/batch_size)) print('timer: {:.4f} sec.'.format(t_epoch_finish - t_epoch_start)) t_epoch_start = time.time() # print("総イテレーション回数:", iteration) return G, D -
ネットワークの初期化
# ネットワークの初期化 def weights_init(m): classname = m.__class__.__name__ if classname.find('Conv') != -1: # Conv2dとConvTranspose2dの初期化 nn.init.normal_(m.weight.data, 0.0, 0.02) nn.init.constant_(m.bias.data, 0) elif classname.find('BatchNorm') != -1: # BatchNorm2dの初期化 nn.init.normal_(m.weight.data, 1.0, 0.02) nn.init.constant_(m.bias.data, 0) # 初期化の実施 G.apply(weights_init) D.apply(weights_init) print("ネットワークの初期化完了") -
学習・検証
# 学習・検証を実行する # 15分ほどかかる num_epochs = 300 G_update, D_update = train_model( G, D, dataloader=train_dataloader, num_epochs=num_epochs)# 生成画像と訓練データを可視化する # 本セルは、良い感じの画像が生成されるまで、何度か実行をし直しています device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu") # 入力の乱数生成 batch_size = 8 z_dim = 20 fixed_z = torch.randn(batch_size, z_dim) fixed_z = fixed_z.view(fixed_z.size(0), fixed_z.size(1), 1, 1) # 画像生成 G_update.eval() fake_images, am1, am2 = G_update(fixed_z.to(device)) # 訓練データ batch_iterator = iter(train_dataloader) # イテレータに変換 imges = next(batch_iterator) # 1番目の要素を取り出す # 出力 fig = plt.figure(figsize=(15, 6)) for i in range(0, 5): # 上段に訓練データを plt.subplot(2, 5, i+1) plt.imshow(imges[i][0].cpu().detach().numpy(), 'gray') # 下段に生成データを表示する plt.subplot(2, 5, 5+i+1) plt.imshow(fake_images[i][0].cpu().detach().numpy(), 'gray')
SAGANによる画像生成の例(上段は教師データ、下段が生成データ)
# Attentiom Mapを出力 fig = plt.figure(figsize=(15, 6)) for i in range(0, 5): # 上段に生成した画像データを plt.subplot(2, 5, i+1) plt.imshow(fake_images[i][0].cpu().detach().numpy(), 'gray') # 下段にAttentin Map1の画像中央のピクセルのデータを plt.subplot(2, 5, 5+i+1) am = am1[i].view(16, 16, 16, 16) am = am[7][7] # 中央に着目 plt.imshow(am.cpu().detach().numpy(), 'Reds')
SAGANの生成器において、画像キャンバス中央のピクセルのAttention Mapの例
(上段は生成データ、下段がAttention Map)
画像キャンバス中央のピクセルを生成する際に、ほかのどの位置のピクセルの特徴量にAttentionをかけて考慮したのかを示している。
参考