以下の論文の解説(まとめ)になります.
DRAW: A Recurrent Neural Network For Image Generation
この論文はDeep Mindの方によるもので,ICML 2015に採択されています.GQNなどの手法と関連が深いため,今回紹介させていただきました.
記事中の図はすべて論文からの引用です.
記事内容に不備がございましたら,ご指摘頂けると助かります.
概要
この論文では,一度の順伝播で画像を生成するのではなく,部分的な生成を反復することで1枚画像を生成する,という特徴を持った深層生成モデルDRAWを提案しています.
例えば人間が絵を描くとき,一部分を描いて,全体のイメージを修正して,また一部分を描く...といった反復的な処理を行っていると考えられます.DRAWではそのような人間にとって自然と思われる過程をモデル化しており,(一度の順伝播で生成を行っている)既存の手法では難しかった高解像度の画像の生成が可能になると期待されます.
DRAWの技術のキモは,以下の2点です.
- encoderとdecoderにRNNを用いることで,反復的な処理を行う際に時系列方向に情報を受け渡している
- Attention機構を用いることで,各時刻で「画像の一部分に注目して他の部分を無視する」ことを,微分可能なモジュールで実現している
以下では,上記の2点に関する詳細を順に説明していきます.
DRAW with RNN
DRAWはVAE(Kingma et al. (2013))に似たネットワーク構造を持っています.
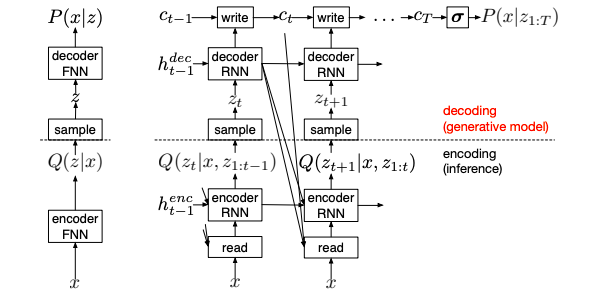
VAE(図左段)では,encoderで入力$x$の情報を持った潜在分布$Q(z|x)$を決定し,decoderで潜在分布$Q(z|x)$からのサンプル$z \sim Q(z|x)$を受け取り,生成分布$P(x|z)$を求めます.
一方,DRAW(図右段)には,VAEとの相違点が3つあります.
- encoderとdecoderはRNNになっている
- encoder,decoderの出力$h^{enc}$,$h^{dec}$は時系列方向に伝搬される
- encoderは前の時刻のdecoderの出力$h^{dec}$も受け取る
- 各時刻のdecoderの出力$h^{dec}$の総和によって,生成分布$P(x|z_{1:T})$が形成される
- VAEでは,一度の順伝播のdecoderの出力によって生成分布が形成されていた
- Attention機構(Read,Writeモジュール)が入力の領域と生成の領域の両方を制限している
ネットワーク構造
以下では,DRAWの主なネットワーク構造について説明しますが,Read・Writeの具体的な処理の定義は次の章で説明します.また,この論文ではRNNモジュールとしてLSTMを採用しています.また以下では,ニューラルネットワークによる線形変換を,単に${\rm output} = W({\rm input})$と表すことにします.
各時刻$t$で,encoderは(Readモジュールを経た)画像入力$x$と前の時刻のencoderの出力$h^{enc}_{t-1}$,decoderの出力$h^{dec}_{t-1}$を入力として受け取ります.ここで,$\hat x_t$は誤差画像を表し,現在のcanvas行列(後ほど定義します)にシグモイド関数を適応したものと入力画像の差分を表します.
\hat x_t = x - \sigma(c_{t-1}) \\r_t = Read(x_t, \hat x_t, h^{dec}_{t-1}) \\h^{enc}_{t} = {\rm RNN}^{enc}(h^{enc}_{t-1},r_t, h^{dec}_{t-1})
encoderの出力$h^{enc}_t$は,潜在分布$Q(z_t|h^{enc}_t)$のパラメータとなります.この論文では,潜在分布に多変量ガウス分布$N(Z_t|\mu_t, \sigma_t)$を仮定しています.そのため,$h^{enc}_t$はガウス分布の平均と標準偏差(の対数)となります.
\mu_t, \log \sigma_t = W(h^{enc}_{t})
各時刻$t$での潜在分布からのサンプル$z_t \sim Q(Z_t|h^{enc}_t)$は,decoderへと入力されます.decoderの出力$h^{dec}_t$は(Write処理を経て),canvas行列$c_t$に累積していきます.時間ステップ$T$後のcanvas行列$c_T$が最終的な生成分布を形成します.
h^{dec}_{t} = {\rm RNN}^{dec}(h^{dec}_{t-1},z_t) \\c_t = c_{t-1} + Write(h^{dec}_{t-1})
Loss
最終的なcanvas行列$c_T$は生成分布$D(X|c_T)$を形成します.例えば,もし入力が2値画像であれば,$D$に平均$\sigma(c_T)$のベルヌーイ分布を用いるのが自然です.連続値の画像であれば,ガウス分布を用います.
生成画像に関するLoss: $L^x$は負の対数尤度になります.
L^x = - \log D(x|c_T)
潜在分布に関するLoss: $L^z$は事前分布$P(Z_t)$と潜在分布$Q(Z_t|h^{enc}_t)$のKLダイバージェンスの総和になります.
L^z = \sum_{t=1}^T KL \left( Q(Z_t|h^{enc}_t)||P(Z_t) \right)
事前分布としては,平均0,分散1のガウス分布を用いることなどが考えられます.
全体のLossは,$L = \langle L^x + L^z\rangle_{z \sim Q}$となります.
画像生成
DRAWでは,事前分布$P(Z_t)$からサンプルして,decoderに入力してcanvas行列に加算していく処理を繰り返すことで,画像生成を行うことができます.
\tilde z_t \sim P(Z_t) \\\tilde h^{dec}_t = {\rm RNN}^{dec}(\tilde h^{dec}_{t-1}, \tilde z_{t-1}) \\\tilde c_{t} = \tilde c_{t-1} + Write(\tilde h^{dec}_{t-1}) \\\tilde x \sim D(X | \tilde c_T)
DRAW with Attention
Attention機構
この論文では,2次元のガウシアンフィルタの行列($N\times N$個の隣接するフィルタ)を適用し,平滑化・スケール変換された画像のパッチ(サイズは$N\times N$)を切り出すことで,Attention機構を実現しています.
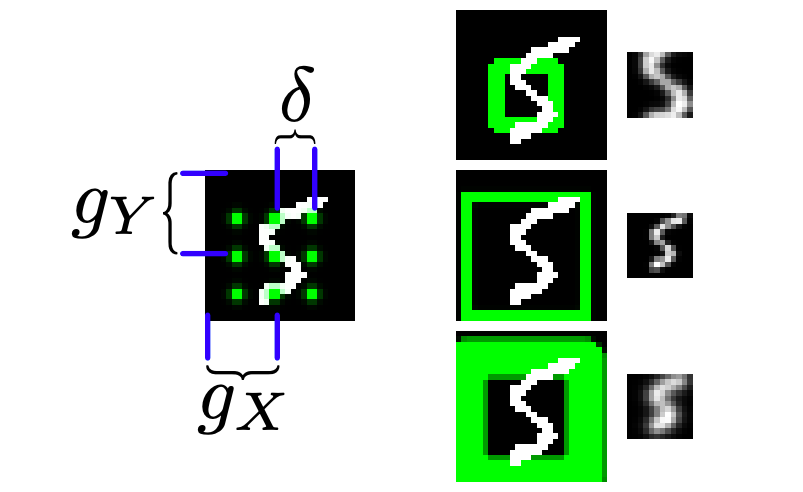
図左段では,画像上に配置された$3\times 3$個の隣接したガウシアンフィルタの例を表しています.隣接したフィルタはストライド$\delta$おきに配置され,中心のフィルタは$(g_X,g_Y)$に位置します.このとき,ストライド$\delta$によってクロップのスケールを変化させています.このとき,$i$行$j$列目のフィルタの中心を$(\mu^i_X, \mu^j_Y)$とします.
さらにAttention機構には,ガウシアンフィルタの分散$\sigma^2$と,フィルタの出力強度$\gamma$の2つのパラメータがあります.図右段では,$12 \times 12$個のガウシアンフィルタのストライド$\delta$と分散$\sigma^2$を変化させた際のフィルタの出力を表しています.(上:($\delta$ 小, $\sigma^2$大),中:($\delta$ 大, $\sigma^2$小),下:($\delta$ 大, $\sigma^2$大)) このとき,1個のフィルタによって1つのピクセルの画素値が計算されるので,出力の画像パッチは$12\times 12$のパッチとなります.
これら5つのパラメータ$(g_X, g_Y, \delta, \sigma^2, \gamma)$は,サイズ$(A, B)$の画像が入力されたとき,前の時刻のdecoderの出力$h^{dec}_{t-1}$に依存して毎時刻計算されます.
(\tilde g_X, \tilde g_Y, \log \tilde \delta, \log \sigma^2, \log \gamma) = W(h^{dec}) \\g_X = \frac{A+1}{2} (\tilde g_X + 1) \\g_Y = \frac{B+1}{2} (\tilde g_Y + 1) \\\delta = \frac{\max (A, B) - 1}{N-1} \tilde \delta
Attentionのパラメータが決まったら,ガウシアンフィルタの行列の処理を定義する行列$F_X$,$F_Y$(それぞれ$N\times A$,$N \times B$)が以下のように計算されます.ただし,$Z_X$,$Z_Y$は正規化パラメータで,$(a,b)$は入力画像上の位置を,$(i,j)$は画像パッチ上の位置を表します.
F_X[i,a] = \frac{1}{Z_X} \exp \left( - \frac{(a-\mu^i_X)^2}{2\sigma^2} \right) \\ F_Y[j,b] = \frac{1}{Z_Y} \exp \left( - \frac{(b-\mu^j_Y)^2}{2\sigma^2} \right)
Readモジュール
Readモジュールでは,入力画像$x_t$と誤差画像$\hat x_t$,前の時刻のdecoderの出力$h^{dec}_{t-1}$を入力として,$N\times N$の画像パッチを2つ($x$,$\hat x$にそれぞれガウシアンフィルタを適用したもの)結合した値を出力します.
Read(x, \hat x, h^{dec}_{t-1}) = \gamma [F_Y x F_X^T , F_Y \hat x F_X^T]
Writeモジュール
Writeモジュールでは,Attention機構のパラメータは$h^{dec}_t$から計算され,Readモジュールと逆順で処理を行います.ただし,$w_t$は生成のための画像パッチになります.
w_t = W(h^{dec}_t) \\Write(h^{dec}_t) = \frac{1}{\hat \gamma}\hat F_Y^T w_t \hat F_X
フィルタの適用例
図左段の$(75, 100)$画像に$12 \times 12$個のガウシアンフィルタを適用してできた$(12, 12)$の画像パッチが,図中段の画像になります.
また,この画像パッチを逆順のフィルタを適用することで再構成した画像が,図右段の画像になります.
検証実験
論文内では,MNISTの生成やSVHMの生成などの検証実験を行っています.定量評価に関しては,負の対数尤度を指標とした評価を行っていますが,ここでは省略します.生成モデルの評価としては再現性と多様性の両方を評価すべきだと思っているので,定量評価としては不十分な気がします.(あくまでも個人的な感想です.)
定性評価に関しては,以下の動画にわかりやすくまとめられています.(画像をクリックすると動画に飛びます.)
結論
この論文では,反復的な処理によって画像の生成を行うDRAWと呼ばれる手法を提案しました.
DRAWの手法の新規性・有用性として,
- encoder,decoderにRNNを用いることで,反復的な画像生成を可能にしたこと
- 微分可能なAttention機構を用いることで,部分的な画像生成を可能にしたこと
が挙げられます.
また,MNISTやSVHMにおける検証実験により,DRAWが既存の手法よりもリアルな画像を生成できることを示しました.