[論文解説] Why Does Hierarchy (Sometimes) Work So Well in Reinforcement Learning?

以下の論文に関する解説(まとめ)になります．

Why Does Hierarchy (Sometimes) Work So Well in Reinforcement Learning?

この論文はGoogle，UC Berkeleyの方によるもので2019年9月にarxivで公開されています．RLの課題と言われている探索について興味深い考察がなされているため，今回紹介させていただきました．

記事中の図はすべて論文からの引用です．
記事内容に不備がございましたら，ご指摘頂けると助かります．

概要

この論文は，主に

1. HIRO(Natchum et al.(2018))などの既存のHierarchical RL(HRL)が通常のRLに比べて優位な要因は，探索の改善によるものだと検証により示した
2. 上の考察から，新たな探索の手法を提案し，通常のRLでも(多くの場合)既存のHRLと同等の性能を出せることを示した

ものになります．

Hierarchical RL(HRL)

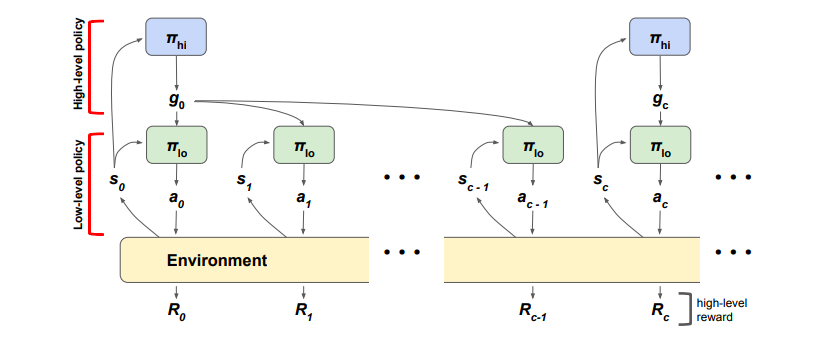
簡単に既存のHRLの説明します．今回は2層のHRLのみを考えますが，本来は3つ以上の階層も考えることができます．

HRLでは，上の図のように上位の方策はcステップごとに上位の行動$g_t$を出力し，下位の方策は毎ステップ下位の行動$a_t$を出力し，環境と相互作用を行い，次の状態$s_{t+1}$と報酬$R_t$を観測します．上位の行動でどのような値を出力するかは手法によって異なるのですが，今回は以下の2つの分類のHRLを考えます．

• Option Framework

  option frameworkのHRLでは，下位に複数(m個)の方策を持ち，上位の方策がどの下位の方策を利用するかを選択する手法になります．すなわち，上位の行動$g_t$は「次のcステップ間にどの下位の方策を利用するか」を表す離散値になります．

  下位の方策では，m個の方策それぞれにQ関数($Q_{low, m}$)を持ち，毎ステップ下記の誤差関数を最小化するようにQ関数を学習し，Q関数を最大化するように方策を学習します．

  $$
  E(s_t, a_t, R_t, s_{t+1}) = \left( Q_{low, m}(s_t, a_t) - R_t - \gamma Q_{low, m}(s_{t+1}, \pi_{low, m}(s_{t+1})) \right)^2
  $$

• Goal-Conditioned

  goal-conditioned HRLでは，下位に1つの方策を持ち，上位の方策が目標状態を出力し，下位の方策は目標状態に近づくように学習を行う手法になります．すなわち，上位の行動$g_t$は「下位の方策が達成すべき状態」を表す連続値になります．なので，option frameworkと違い，下位の方策やQ関数は目標状態$g_t$にも依存した出力を行うことになります．

  下位の方策では，毎ステップ下記の誤差関数を最小化するようにQ関数を学習し，Q関数を最大化するように方策を学習します．ここで$r_t$は目標状態と現在の状態のL2ノルムのマイナス倍など，目標状態にどれだけ近いかを表し，環境から陽に与えられないintrinsic rewardになります．

  $$
  E(s_t, g_t, a_t, r_t, s_{t+1}, g_{t+1}) = \left( Q_{low}(s_t, g_t, a_t) - r_t - \gamma Q_{low}(s_{t+1}, g_{t+1}, \pi_{low}(s_{t+1}, g_{t+1})) \right)^2
  $$

option framework，goal-conditioned共に，上位の方策はcステップごとの遷移$(s_t, g_t, R_{t:t+c-1},s_{t+c})$をもとにTD誤差を最小化するようにQ関数を学習し，Q関数を最大化するように方策を学習します．

また，この論文では$(s_t, a_t, R_{t:t+c-1}, s_{t+c})$の遷移を用いた通常のRLも検証しています．本記事中ではmulti-step rewardsという単語を，cステップごとの(とびとびの)transitionを用いる手法を指すことにします．

タスク

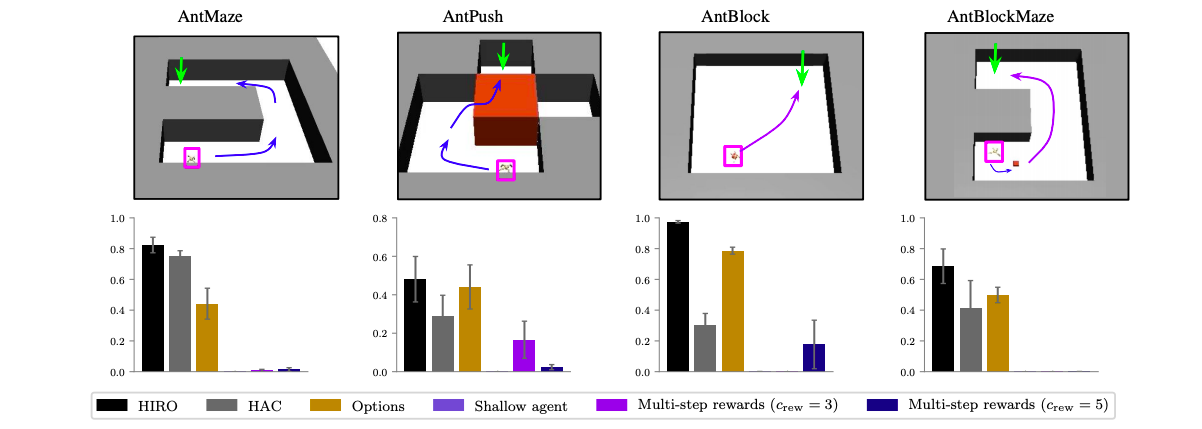
この論文では，検証実験に4つの四脚エージェントのナビゲーションタスクを用いています．AntMazeとAntPushでは，エージェント(紫)がゴール(緑色)まで進む，というタスクになります．AntBlockとAntBlockMazeでは，小さいブロックを押してゴールまで運ぶタスクになります．

図下段のグラフは，既存のHRL(HIRO，HAC，Options)と通常のRL(TD3)で学習した時のタスク成功率を表しています．ただし，TD3ではmulti-step rewards($c=3, 5$)を用いた場合の結果も載せています．

また以降の検証実験では，HRLではHIROを，通常のRLではTD3を用いることにします．

HRLの優位性

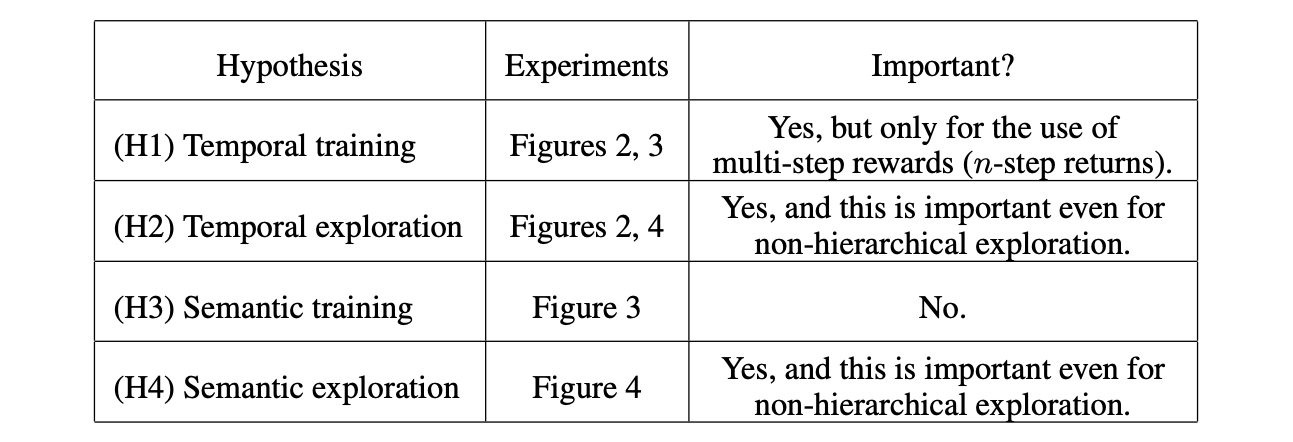
この論文では，HRLが通常のRLに比べて優位な要因に関して，以下の4つの仮説を立てています．

• H1: Temporally extended training
  • 学習の時定数を大きくする(cステップに1つの遷移を使う)ことで，実質のエピソードの長さが短くなり，報酬の伝搬が効率的になり学習がしやすくなる
• H2: Temporally extended exploration
  • 上位の行動の時定数を大きくすることで，実際に環境に適用される下位の行動の探索に時間相関が生まれる
• H3: Semantic training
  • 上位の行動は，下位の行動よりも抽象的で意味のある行動(系列)を表していると考えられるため，学習がしやすくなる
• H4: Semantic exploration
  • 上位の行動は，下位の行動よりも抽象的で意味のある行動(系列)を表していると考えられるため，より意味のある探索が期待できる
  • 例えば，下位の行動はロボットの関節のトルクを表し，上位の行動は目標状態の(x, y)座標を表すとすると，(x, y)座標を表す行動空間で探索をした方が意味があると考えられます

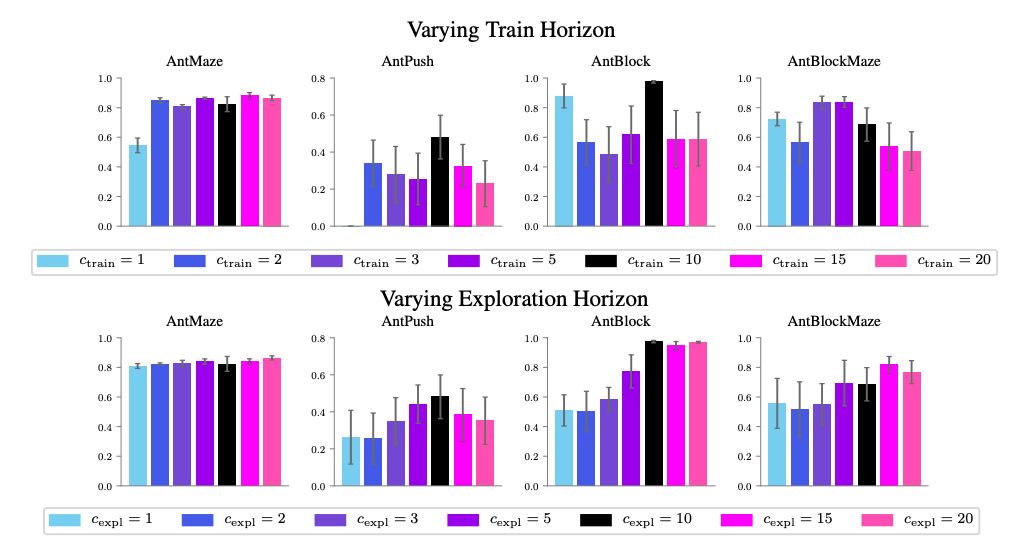
検証実験①

ここでは，仮説のうちH1とH2に着目し，時定数の変化によるHRLの優位性の変化を検証します．HRLの手法としてHIROを用い，上位の方策の時定数cを変化させます．このときcは

• 上位の方策の報酬$R_{t:t+c-1}$の変化による学習への寄与(H1に対応)
• 上位の方策の行動のサンプリング頻度の変化による探索への寄与(H2に対応)

の2つの部分において影響を与えますが，それぞれは独立に変化させることができるので，それぞれを$c_{train}$，$c_{expl}$とします．それぞれのパラメータを変化させた時のタスク成功率の数を示します．(デフォルトは$c=10$)

論文では，上記の結果から以下のような考察をしています．

• 図上段の結果(H1に対応)
  • AntMazeやAntPushでは$c_{train}=1$と$c_{train}>1$の間で大きな差があるが，$c_{train}>1$の間では特に傾向はみられない
  • AntBlock等では傾向は得られていない
• 図下段の結果(H2に対応)
  • AntMaze以外のタスクでは，$c_{expl}$が大きいほど性能が良くなる傾向が見られる
  • $c_{expl}=1$でも通常のRLに比べて性能が良くなっている(本記事2つ目の図下段参照)ので，時定数の変化以外にも要因があるはず

まとめると，

• H1の仮説は概ね正しいと考えられるが，多くの場合$c_{train} > 1$であれば十分
• H2の仮説は正しいと考えられるが，時定数の変化以外にも要因があるはず

検証実験②

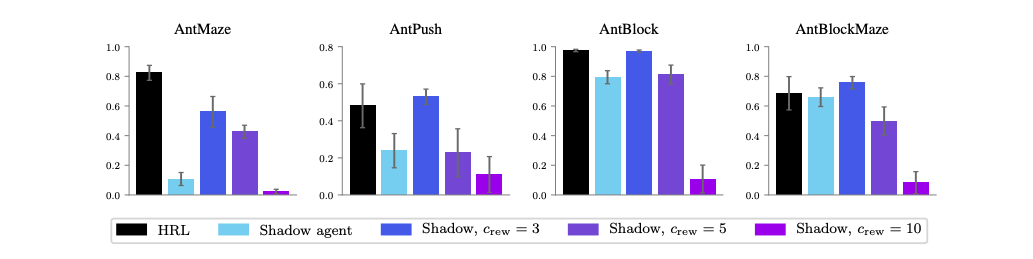
ここでは，仮説のうちH3に着目し，上位の方策がより意味のある行動空間を持つことによる学習への影響を検証します．

この実験では，探索の要因(H2，H4)を排除して検証を行うために，

1. HRLエージェントと並行して，通常のエージェント(shadow agent)も用意する
2. 通常のエージェントを，HRLエージェントが集めたデータ(transition)も使って学習する

ことを行います．通常のエージェントをHRLの探索で得たデータも使って学習することで，H2とH4の影響を排除しているので，この実験のHRLの優位性の要因はH1とH3によるもののみだと考えられます．

また，この実験ではH1による要因を(できるだけ)排除するため，通常のエージェントをmulti-step rewards($c=3,5,10$)を使って学習させたものも検証しています．そのため，もし通常のエージェント(multi-step rewardsあり)がうまく学習できるのであれば，H3による優位性は認められないことになります．

論文では，上記の結果から以下のような考察をしています．

• 多くの場合(AntMaze以外)，通常のRLでも適切なmulti-step rewardsを用いることで，HRLと同様の性能を出せる

まとめると

• H3は，HRLの優位性を説明する主な要因ではない
• H1による優位性は，適切なmulti-step rewardsを用いることで通常のRLでも再現できる
• よって，主なHRLの優位性は探索の改善にある

提案手法

上の検証実験2つから，主なHRLの優位性は探索の改善にあると考えられます．この論文では，この考察からヒントを得た，通常のRLにおける探索の手法を2つ提案しています．

• Explore & Exploit

  Explore & Exploitでは「ゴールに近くこと」が良い探索方針だと考え，エージェントを2つ用意します．一方は通常のRL同様，報酬を最大化するように学習し，他方はゴールに近くように学習します．ただし，このゴールは，平均回帰過程(Ornstein–Uhlenbeck process)からランダムにサンプルします．

  行動選択の際には，$c_{switch}$ステップごとに2体のエージェントをそれぞれ${0.8, 0.2}$の確率で選択し，その後$c_{switch}$ステップ間は同じエージェントで行動します．学習の際には同じリプレイバッファを用いて，学習を行います．

  上記の手法によって，goal-conditioned HRLの抽象的で意味のある探索を階層のないRLで再現しています．

• Switching Ensemble

  Switching Ensembleでは，複数(e.g. 5)のエージェントを用意します．行動選択の際には，$c_{switch}$ステップごとにエージェントを一様な確率で選択し，その後$c_{switch}$ステップ間は同じエージェントで行動し，学習の際には同じリプレイバッファを使って学習します．

  上記の手法によって，option frameworkのoptionsを階層のないRLで再現しています．

また，上記の2つの手法では両者ともにH2の「時間相関を持った探索」を行っていると考えることができます．

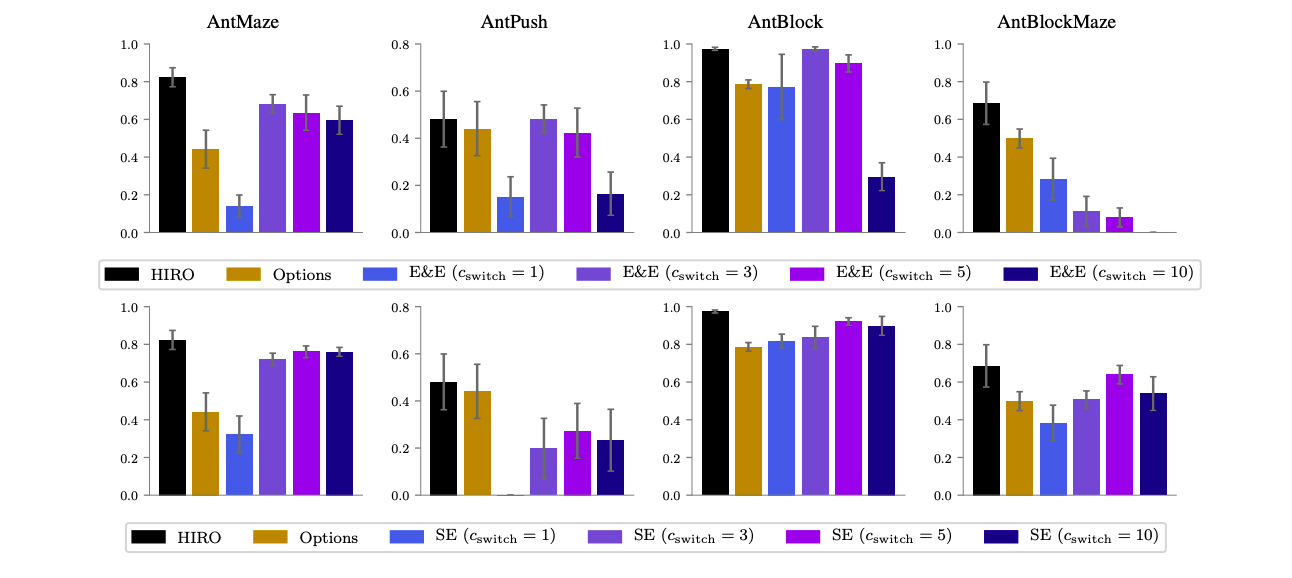
検証実験③

提案手法であるExplore & ExploitとSwitching Ensembleを通常のRL(TD3)と組み合わせて用いることで，既存のHRLと比較して検証します．

論文では，上記の結果から以下のような考察をしています．

• Explore & ExploitではAntBlockMaze以外で，Switching EnsembleではAntPush以外で，HRLと同等の性能を出している

まとめると，

• ①multi-step rewardsを使う，②時間相関を持った探索を行う，の2つを満たすことで，(多くの場合)通常のRLでもHRLと同様の性能を出すことができる

結論

この論文では，HRLの優位性の要因として，上の4つの仮説を立てて検証を行いました．

検証の結果，

• H1の「学習の時定数を大きくする(cステップに1つの遷移を使う)こと」による優位性は重要だが，通常のRLにおいてもmulti-step rewardsを用いることで同等の性能を再現できる．すなわち，HRLの優位性は全て「探索の改善」によるものだと考えられる
• H2，H4の「探索の改善」による優位性は重要だが，通常のRLでも時間相関を持った探索(Explore & Exploit，Switching Ensemble)を用いることで，同等の性能を出すことができる

ことが示されました．