教科書とかでニューラルネットのback propagation(誤差逆伝播法)の説明を読んで、式を眺めてなんとなく分かったような気になっていても時間が経つと忘れてしまう。
なので一回数式をまとめて、ついでにC++でスクラッチから実装して残しておくことにした。
back propagationの導出と実装をいっぺんやればさすがに頭に残るだろうと期待。
何でもかんでもこういうノリでゆっくりやる訳にはいかないが、基本の部分はやっといてもいいのではないかと。
数式的なもののメモ
ベクトルはすべて縦ベクトル。数式と疑似コードっぽいのが混じっているが心の目で読むべし。
深層学習 (機械学習プロフェッショナルシリーズ)の記法にほぼ倣っているが、実装時の混乱を避けるために第0層から始まることにしている等多少の変更あり。
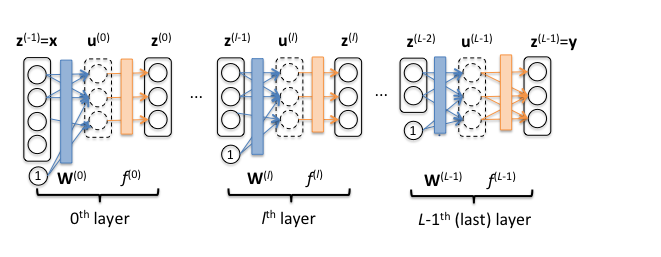
$L$: 入力層を除く全体の層数。各層は$l$($0 \le l < L$)で表す。
${\bf x}$: ネットワーク全体への入力。 便宜的に${\bf z}^{(-1)}={\bf x}$と考える。
${\bf y}$: ネットワーク全体からの出力。
${\bf d}$: 目標出力(正解ラベル)。
${\bf W}^{(l)}$: 第l層の重み行列。
${\bf u}^{(l)}$: 入力${\bf x}^{(i)}$に重み行列${\bf W}^{(l)}$をかけた後のやつ。
$f^{(l)}$: 第$l$層の活性化関数。${\bf u}^{(l)}$を入れると${\bf z}^{(l)}$が出てくる感じのやつ。
${\bf z}^{(l)}$: ${\bf u}^{(i)}$を活性化関数$f^{(l)}$に通した後のやつ。${\bf z}^{(L-1)}$はネットワーク全体の出力ということになるので${\bf y}$と等価。
$L$: 損失関数。卑近な範囲では二乗誤差かクロスエントロピーのどちらか。
ベクトルと行列のサイズ(次元数)について:
${\bf u}^{(l)}$と${\bf z}^{(l)}$のサイズは同じ。
${\bf W}^{(l)}$は${\rm len}({\bf u}^{(l)})$ 行 $({\rm len}({\bf z}^{(l-1)})+1)$列。
${\bf x}$と${\bf y}$のサイズは選べないが、$0\le l < L-1$について${\bf u}^{(l)}$(中間層)のサイズはネットワークの設計者の好きに選ぶことができ、これに応じて${\bf W}^{(l)}$のサイズが決まる。
順伝播
$0\le l < L$の範囲の全ての$l$について:
{\bf u}^{(l)}={\bf W}^{(l)}\cdot[{\bf z}^{(l-1)};1]
(ここで、$\cdot$は行列積で$[{\bf z}^{(l-1)};1]$はベクトルの末尾にバイアス項に対応する1をくっつけたものという雰囲気)
{\bf z}^{(l)}= f({\bf u}^{(l)})
最終出力
{\bf y}= {\bf z}^{(L-1)}
$L$がcross entropy loss functionのときの損失
L({\bf y}, {\bf d})=\sum_i {d_i \log(y_i)}
back propagation (誤差逆伝播法)
目的: $\frac{\partial L}{\partial w^{(l)}_{ij}}$をすべての$i$, $j$, $l$について求めること。そうするとラベルつき学習データ(${\bf x}$, ${\bf y}$)から最急降下(や他のもっとスマートな非線形最適化アルゴリズム)で${\bf W}^{(l)}$の学習を行うことができる。
大事な登場人物: ${\bf \delta}^{(l)}$を下記のように定義する。(${\bf \delta}^{(l)}$はベクトルで$\delta^{(l)}_i$はその要素)
\delta^{(l)}_i=\frac{\partial L}{\partial u^{(l)}_i}
すべての${\bf \delta}^{(l)}$がわかっていれば$\frac{\partial L}{\partial w^{(l)}_{ij}}$は下記のように容易に求まる。
\frac{\partial L}{\partial w^{(l)}_{ij}}=\frac{\partial L}{\partial u^{(l)}_i}\cdot\frac{\partial u^{(l)}_i}{\partial w^{(l)}_{ij}}
=\delta^{(l)}_i\cdot [z^{(l-1)}_j; 1] \cdots (★)
(ここで、
u^{(l)}_i=\sum_j w^{(l)}_{ij} \cdot [z^{(l-1)}_j; 1]
のため
\frac{\partial u^{(l)}_i}{\partial w^{(l)}_{ij}}=[z^{(l-1)}_j; 1]
であることを利用している。)
${\bf \delta}^{(l)}$を求めるには、出力層の${\bf \delta}$(つまり${\bf \delta}^{(L-1)}$)をまず求めそこから入力層側に順次遡っていく。
出力層がsoftmaxで誤差関数がcross entropyのとき${\bf \delta}^{(L-1)}$は以下の通り(導出略。微分をがんばれば求まる、はず)
\delta^{(L-1)}_i=y_i - d_i \cdots (★★)
$0 \le l \le L-2$の範囲の$l$について、
\delta^{(l)}_i=\frac{\partial L}{\partial u^{(l)}_i}
=\sum_k\frac{\partial L}{\partial u^{(l+1)}_k} \cdot \frac{\partial u^{(l+1)}_k}{\partial u^{(l)}_i}
=\sum_k{\delta^{(l+1)}_k \cdot (w^{(l+1)}_{kj}f'(u^{(l)}_j))} \cdots (★★★)
(ここで、
u^{(l+1)}_k=\sum_j{w^{(l+1)}_{kj}z^{(l)}_j}=\sum_j{w^{(l+1)}_{kj}f(u^{(l)}_j})
なので、
\frac{\partial u^{(l+1)}_k}{\partial u^{(l)}_i}=w^{(l+1)}_{kj}f'(u^{(l)}_j)
であることを利用している。)
$f$はReLuなりsigmoidなりtanhなりの既知の関数なので$f'$は解析的に求められる。
なので、まず入力層から出力層への準伝播で${\bf u}^{(l)}$と${\bf y}$を求めたのちに、
(★★)から始め(★★★)を再帰的に適用してすべての${\bf \delta}^{(l)}$を求め、それを使って(★)によりすべての$\frac{\partial L}{\partial w^{(l)}_{ij}}$を求めることができる。
実装
C++14で上記の式に従って実装。実用は考えていないので標準ライブラリだけ使い、積和演算はすべてforループ。アルゴリズムは(読み返した時の自分は)追いやすいと思われるがミニバッチごとにtensor演算をするような書き方にしていないので遅い。
活性化関数はReLuとsigmoidと(ちょっと好奇心で)swishを実装。
出力層はとりあえずsoftmaxのみ。
fully connected layerを単純に積んだ場合だけに対応。
こんな感じでネットワーク定義が書けるようにした。
Network<double> net;
net.addLayer(28*28, 300, Layer<double>::ActivationType::RELU);
net.addLayer(300, 10, Layer<double>::ActivationType::SOFTMAX);
あと、ほんとうはgradient checkingとかするべきなのだがやっていない。
実験
折角なのでmnistを学習させてみた。
学習データは60,000画像、テストデータが10,000画像。
入力画像が各画素8bitグレースケールの28*28なので、各画素を[0, 1]のdoubleに正規化したうえでこれを1つの784次元のベクトルとしてニューラルネットの入力とし、0から9の10値出力を10次元のsoftmax出力層とする。
損失関数はcross entropy。
300次元の隠れ層1つ、活性化関数はReLu。(入力層を1層と数える言い方でいう3層ネットワーク)
最適化は単純なSGD。ミニバッチサイズ100。正則化とかもなんにもなし。learning rate0.2から始め、学習データ損失が前のepochより増えたらlearning rateを半分にする。
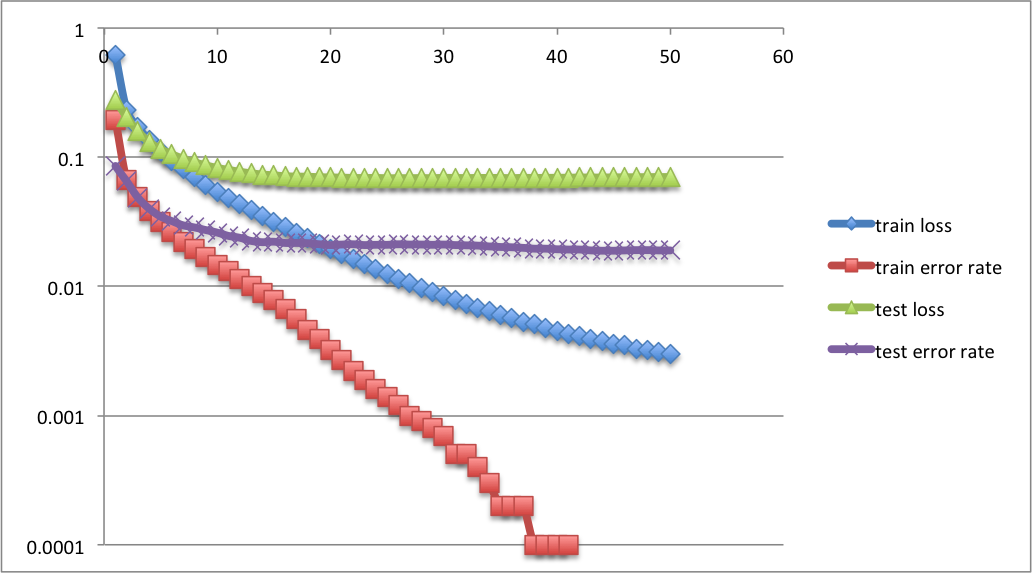
50epoch回してtest set error rateが1.9%くらいになった。
mnistのページによると3-layer NN, 500+300 HU, softmax, cross entropy, weight decay(隠れ層2つなので入力層・出力層を数える言い方だと4層ネットワーク)でerror rate1.53%くらいらしいので、まあまあ妥当な精度に見える。
隠れ層を増やしてみた。
300+300 2 hidden layers:
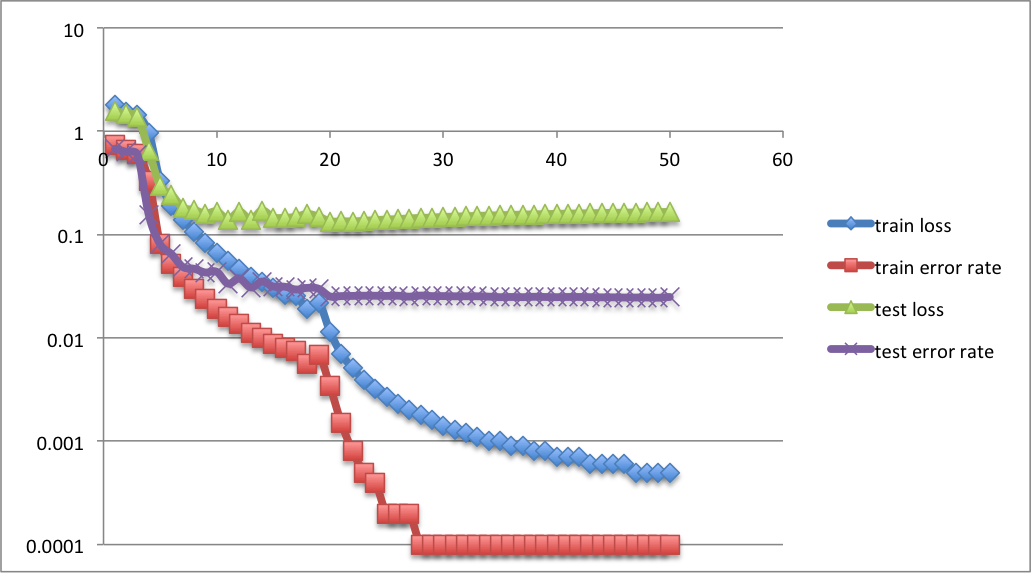
隠れ層2層では途中でtest lossが途中から増加しているのでoverfittingが起こっていることがわかる。test error rateはよいところでも2.4%-2.5%くらい。
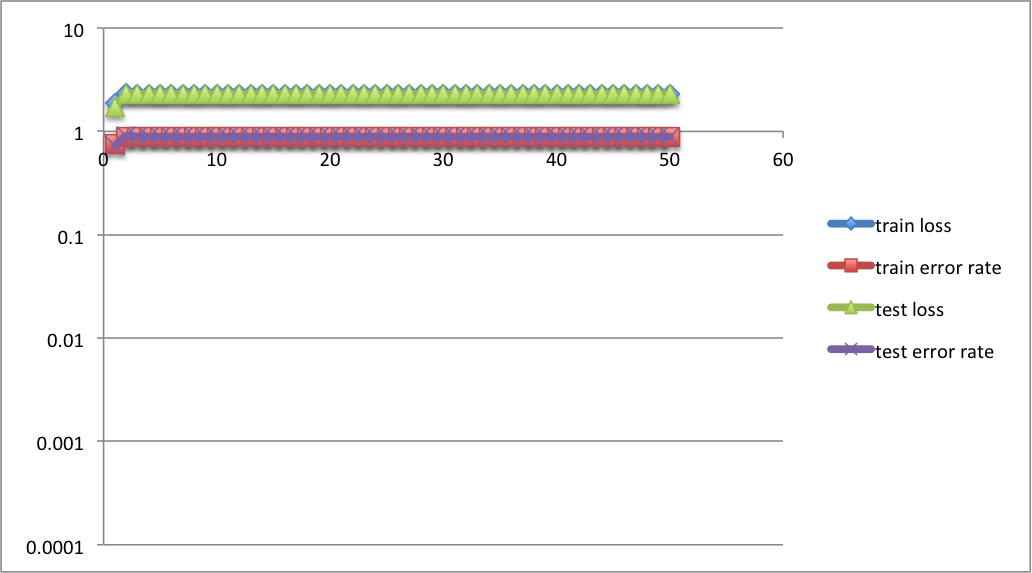
隠れ層3層では(図には現れていないが)勾配消失のため全く学習が進まない。