Go で Tenka1 2018 Beginner, C - Align を解いてみた

Go で Tenka1 2018 Beginner C - Align を解いてみました。

問題

問題文

整数が N 個与えられます。i 個目の整数は Ai です。 これらを好きな順に一列に並べるとき、隣り合う要素の差の合計の最大値を求めてください。

制約

• $2 \le N \le 10^5$
• $1 \le A_i \le 10^9 $
• 入力は全て整数である。

( https://atcoder.jp/contests/tenka1-2018-beginner/tasks/tenka1_2018_c より引用)

考えたこと

より小さいものと大きいものを隣り合わせるのが良さそう？
→ Aをソートして真ん中から大きい方、小さい方交互に埋めていけばいいんじゃね？
→ 大きい方を真ん中にするか、小さい方を真ん中にするか、Nの偶奇でいくつかパターンがあるので、全部計算して一番大きいやつ
でも、証明できないなーと思いつつサブミットしたらやはりWAでギブアップ。証明重要ですね。

正しい考え方

公式解説によれば、
最適な並び順を

$p_1, p_2, p_3, p_4, \dots , p_n $

とすると、この数列は

$p_1 \ge p_2 \le p_3 \ge p_4 \le \dots $

または

$p_1 \le p_2 \ge p_3 \le p_4 \ge \dots $

のどちらかの関係になっているはずです。

最適な並び順における大小関係

これは、次のように考えると正しいことがわかります。

数列に $ \dots \ge p_{i-1} \le p_i \le p_{i+1} \ge \dots$ という並びが存在したとします。隣り合う数字の差分はそれぞれ
$d_1 = p_i - p_{1-1}$
$d_2 = p_{i+1} - p_{i}$
であり合計は $d_1 + d_2$ です。（$d_i$ はいずれも0または正の数）

ここから $p_{i}$ を取り除き、列の末尾に移動したとすろと
$\dots \ge p_{i-1} \le p_{i+1} \ge \dots $
となり、 数字の差分は
$d_3$
$= p_{i+1} - p_{i-1}$
$= p_{i+1} - p_i + p_i - p_{i-1} $
$= d_2 + d_1$
となります。つまり差分の合計値として、この部分については $p_i$ があってもなくても変わりありません。

一方で、 $p_i$ を移動した先の列の末尾においてはどうなるでしょうか。
ここでは複数の可能性が考えられます。
もし

$p_{n-1} \le p_n \ge p_i$

であれば、もとの数列よりも $p_n - p_i$ の分だけ差分の合計値が0以上増加することになります。
もし

$p_{n-1} \le p_n \le p_i$

であれば、やはり、$p_i - p_n$ という0以上の値の分だけ差分の合計値が増加することになります。また、この場合はさきほどと同様、

$p_{n-1} \le p_i \ge p_n$

のように間にある $p_n$ を取り除き、末尾に移動することで、更に差分の合計値を増やすことが可能です。
もともとの末尾が

$p_{n-1} \ge p_n$

だったとしても、同様に考えれば、 差分の合計値が増えることは合っても、減ることはありません。
というわけで、最適な並び順における大小関係は最初に示したとおりの形になります。

最適な並び順

さて、最適な数列において、数字が

$p_1 \ge p_2 \le p_3 \ge p_4 \le \dots $

または

$p_1 \le p_2 \ge p_3 \le p_4 \ge \dots $

と並んでいるとき、隣り合う数字の差の合計はそれぞれ

$ (p_1 - p_2) + (p_3 - p_2) + (p_3 - p_4) + (p_5 - p_4) + \dots $
$ = p_1 - 2\times p_2 + 2\times p_3 - 2\times p_4 + 2\times p_5 - \dots $

または

$ (p_2 - p_1) + (p_2 - p_3) + (p_4 - p_3) + (p_4 - p_5) + \dots $
$ = - p_1 + 2\times p_2 - 2\times p_3 + 2\times p_4 - 2\times p_5 + \dots $

となります。この式からは、直感的につぎのことがわかります。

• 両端以外にある数字は、2倍したうえで足されるグループと、2倍したうえで引かれるグループに分かれる
• 両端にある数字はそのまま足されるグループと、そのまま引かれるグループに分かれる

ただし、$N$ の大きさや偶奇によって各グループの要素数が0になることはあります。例えば $N=3$ で $p_1 \lt p_2 \gt p_3 $ が最適な並びなら、 2倍で足されるグループは $p_2$ , 2倍で引かれるグループは空、そのまま足されるグループは空、そのまま引かれるグループは $p_1, p_3$ となります。

また、

• より大きい数は、そのまま足すよりも2倍して足したほうが良い
• より小さい数は、そのまま引くよりも、2倍して引いたほうが良い（大きい数を2倍して引くよりも、小さいを2倍して引いたほうがマシ）

のは明らかなので、

• 中央値に近い値を両端（そのまま足す、または引くグループ）に持ってくる
• 両端以外は中央値よりも大きい数（2倍して足すグループ）と、中央値よりも小さい数（2倍して引くグループ）を交互にならべる

と最適になることがわかります。

実装

$A$ をソートしたあと2分割して、もともと中央値側にあった値が新しい両端にくるように交互に組み合わせるようにすると最適になります（図1）。

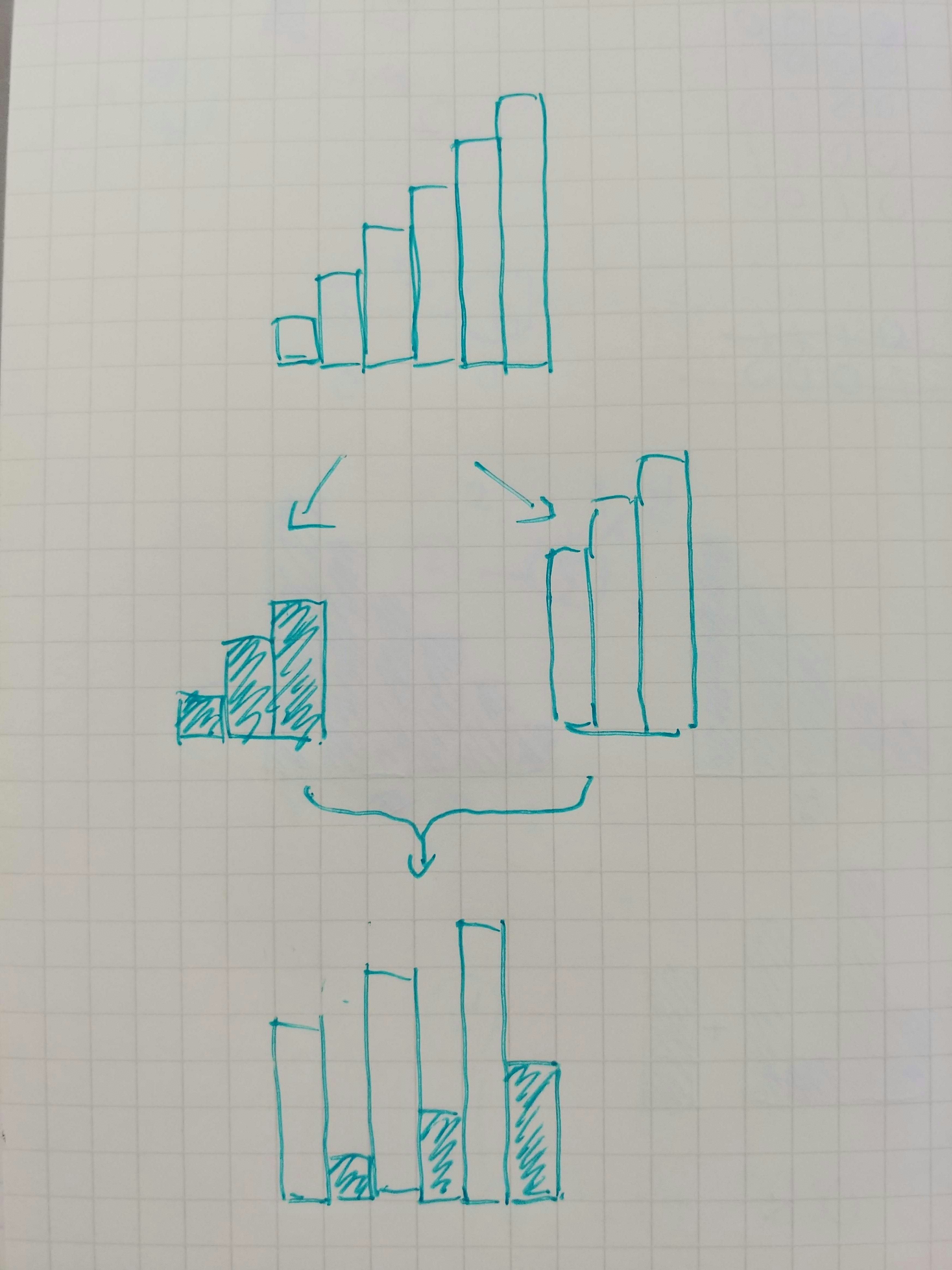
ただし、これは中央値がちょうど2つある、 $N$ が偶数の場合です。
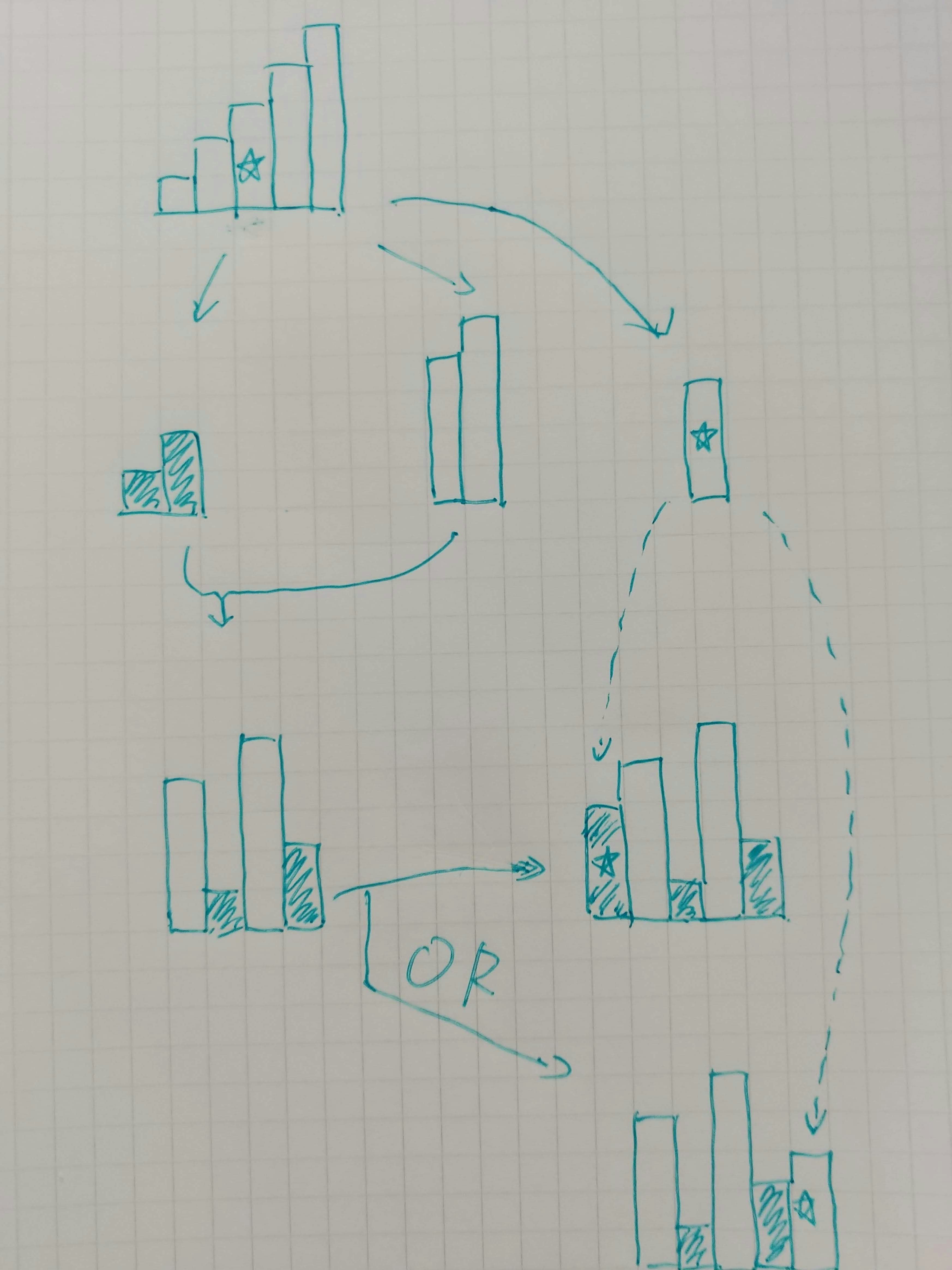
$N$ が奇数の場合は中央値が1つなので、中央値の上か下の数のどちらかを端の数字として使う必要があります。このため、中央値以外の数を $N$ が偶数のときと同じように組み合わせた後、中央値を足す側のグループに含める場合と、引く側のグループに含める場合のどちらが最適になるのかを調べる必要があります（図2, ☆が中央値）。

提出コード

最終的に次のようなコードを書きました（抜粋）。全体はこちら

func main() {
    defer stdout.Flush()
    N := readInt()
    A := make([]int64, N)
    for i := range A {
        A[i] = readInt64()
    }
    Sort(A, func(i, j int) bool { return A[i] < A[j] })

    small := make([]int64, N/2)
    large := make([]int64, N/2)
    m := N / 2
    if N%2 == 1 {
        m++
    }

    for i := 0; i < N/2; i++ {
        small[i] = A[i]
    }

    for i := 0; i < N/2; i++ {
        large[i] = A[m+i]
    }

    b := make([]int64, 0, N)
    for i := 0; i < N/2; i++ {
        b = append(b, large[i])
        b = append(b, small[i])
    }

    ans := calc(b)

    if N%2 == 1 {
        ans += max(b[0]-A[N/2], A[N/2]-b[len(b)-1])
    }
    println(ans)
}

func max(a, b int64) int64 {
    if a < b {
        return b
    }
    return a
}

func abs(a int64) int64 {
    if a < 0 {
        return -a
    }
    return a
}

func calc(a []int64) int64 {
    var ans int64
    for i := 0; i+1 < len(a); i++ {
        ans += abs(a[i] - a[i+1])
    }
    return ans
}

$N$ が奇数の場合は、実際には完全な数列を構成せず、中央値を取り除いて偶数の場合と同様に構成したあと、取り除いた中央値を両端どちらにつけたほうが最大になるかだけをチェックしています。