ディープラーニングで使う活性化関数を可視化してみた

自分用のメモ

なんか調べたら同じような記事があったけど気にしない。
同じ本を参考にしたから仕方ない

ステップ関数

閾値より小さかったら0、大きかったら1を返す（今回の例では0を閾値とする）

h(x)=\begin{cases}
  0\quad(x \leqq 0) \\
  1\quad(x > 0)
\end{cases}

def step_function(x):
    return np.array(x > 0, dtype = np.int)

x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)

plt.plot(x, y)
plt.show()

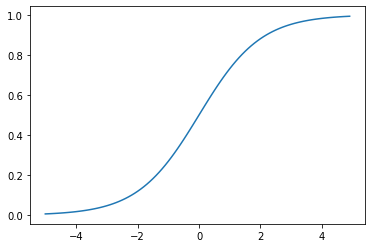
シグモイド関数

ステップ関数の上位互換
値を0~1にスケールする

h(x) = \frac{1}{1 + e^{-x}}

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)

plt.plot(x, y)
plt.show()

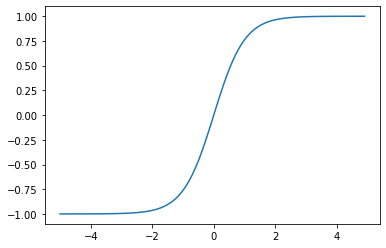
tanh関数

シグモイド関数の上位互換。
勾配消失問題が起こりにくいように線形変換させたけどやっぱり勾配消失問題が起こることもあるらしい

h(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}

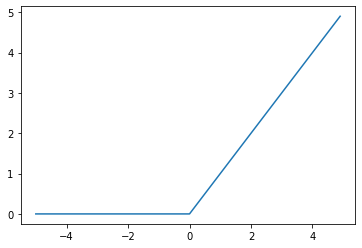
ReLU関数

tanh関数の上位互換。
0以下だったら0、0より大きかったら入力した値をそのまま返す

h(x)=\begin{cases}
  0\quad(x \leqq 0) \\
  x\quad(x > 0)
\end{cases}

def relu(x):
    return np.maximum(0, x)

x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)

plt.plot(x, y)
plt.show()

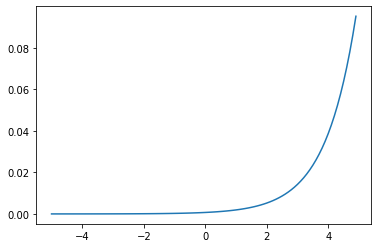
ソフトマックス関数

0~1で総和が1になるように返してくれるやつ。確率っぽく扱えるようになるから出力層で使われがち。大小関係が変わらないから使う必要はないって言ってる人もいる

y_k = \frac{e^{a_k}}{\sum_{i=1}^ne^{a_i}}

def softmax(a):
  exp_a = np.exp(a)
  sum_exp_a = np.sum(exp_a)
  y = exp_a / sum_exp_a
  return y

x = np.arange(-5, 5, 0.1)
y = softmax(x)
plt.plot(x, y)
plt.show()

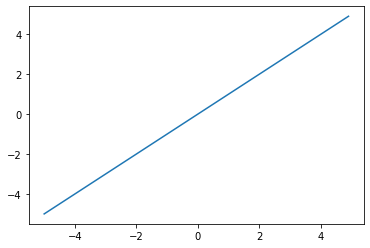
恒等関数

入力された値をそのまま返すやつ。趣深い。いとをかし。

h(x)=x

def identity_function(x):
    return x
x = np.arange(-5, 5, 0.1)
y = identity_function(x)
plt.plot(x, y)
plt.show()