胡散臭いタイトルですがガチです。
（シミュレーション方法等間違っていたらコメントで教えてください）

TL;DR

LightGBMを用いて翌日のトヨタ株の終値が予測実行日の終値よりも、上がる or 下がるの二値分類を実施
上がる場合は株を買う、下がる場合は株を売る、という処理を毎日実施
2020/01/01~2020/12/31の実績を用いて売買のシミュレーションを行ったところ、年利30.2299%のプラスとなった

背景

仕事をサボりながらネットサーフィンをしていたら面白そうな論文を発見。

当論文は2008年の発表で、予測モデルはSVMを使用している。

そこで、2008年以降に発表されたモデル(今回はLightGBM)で予測する実験を行う。

また、該当論文では、日経平均株価を予測対象としているが、今回は実際の取引を想定して、トヨタ自動車株式会社の株価を予測対象とする。

実験環境

Google Colab

使用データ

トヨタ自動車株式会社の株価
日経平均株価
NYダウ
新興国株式インデックス指数(MSCI エマージング・マーケット・インデックス)
ドル円相場

いずれも2018/01/01~2020/12/31の日足のデータを使用する。
(使用データの期間に特別な意図はないため、期間を変えることでシミュレーション結果の改善に繋がる可能性が考えられる。)

必要なライブラリのimport

Python3

%pip install optuna 

import codecs

import numpy as np
from matplotlib import pyplot as plt
import pandas as pd
from sklearn import metrics

import optuna.integration.lightgbm as lgb

データの読み込み

それぞれのcsvを読み込んで結合

Python3

# データの読み込み
def csv_to_df(path):
  with codecs.open(path, "r", "UTF-8", "ignore") as file:
      df = pd.read_table(file, delimiter=",")
  return df

nikkei = csv_to_df("nikkei_stock_average_daily_jp.csv")
nydow = csv_to_df("nydow.csv")
usdjpy = csv_to_df("usdjpy_d.csv")
shinko = csv_to_df("shinko.csv")
toyota = csv_to_df("toyota.csv")

# csvの結合
for name, df in zip(["nikkei", "nydow", "usdjpy", "shinko", "toyota"],[nikkei, nydow, usdjpy, shinko, toyota]):
  df.iloc[:, 0] = pd.to_datetime(df.iloc[:, 0])
  columns_list = list(df.columns)
  columns_dict = {columns_list[0]:"date"}
  for column in columns_list[1:]:
    columns_dict[column] = f"{name}_{column}"
  df = df.rename(columns=columns_dict)

  if "data" not in globals():
    data = df
  else:
    data = pd.merge(data,df)

# 日付順にソート
data = data.sort_index()

特徴量の作成

今回の予測では、株価の値動きに注目するため、前日比と直近5日間の加重平均との差分を特徴量に加える

Python3

def weighted_average(df):
  ans = df*0
  for i in range(1,6):
    ans += ((6 - i) * df.shift(i) / 15)
  return ans


for column in list(data.columns)[1:]:
  # 直近5日間の加重平均との差分
  data[f"{column}_diff_5Dmean"] = (data[column] - weighted_average(data[column]))
  # 前日比
  data[f"{column}_DoD"] = data[column] / data[column].shift(1)

また、正解データとして、翌日の終値が当日の終値を上回っていた場合は1、そうでない場合は0とする。

Python3

data["y"] = ((data["toyota_終値"] - data["toyota_終値"].shift(-1)) < 0)*1

訓練データの作成

今回は、2020年のデータをテストデータ、それ以前のデータを訓練データとする。

Python3

train = data[data["date"] < "2020-01-01"]
test = data[("2020-12-31" >= data["date"]) & (data["date"] >= "2020-01-01")]

train = train.set_index('date')
test = test.set_index('date')

lgb_train = lgb.Dataset(train.drop("y", axis=1), train["y"])
lgb_eval = lgb.Dataset(test.drop("y", axis=1), test["y"], reference=lgb_train)

予測を実行

ハイパーパラメータチューニングのため、optuna.integration.lightgbmを使用

Python3

params = {
    'objective': 'binary',
    'metric': 'auc',
    "verbosity": -1,
    "boosting_type": "gbdt",
}

gbm = lgb.train(params,
                lgb_train,
                num_boost_round=99999999,
                valid_sets=[lgb_train, lgb_eval],
                early_stopping_rounds=10
               )

モデルの評価

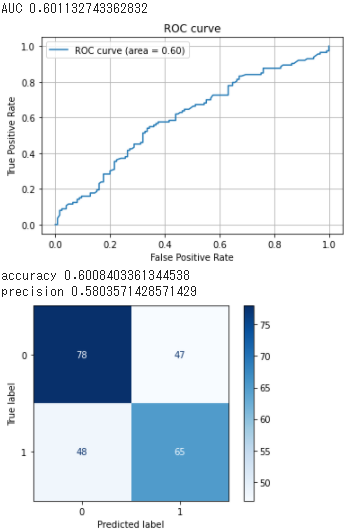
モデルの精度自体はイマイチ（といっても、人間が予測をした際の精度がどのくらいになるのかによって、評価は変わるが）

Python3

# テストデータに対し予測を実施
y_pred = gbm.predict(test.drop("y", axis=1), num_iteration=gbm.best_iteration)
# AUCを計算
fpr, tpr, thresholds = metrics.roc_curve(np.asarray(test["y"]), y_pred)
auc = metrics.auc(fpr, tpr)
print("AUC", auc)

# ROC曲線をプロット
plt.plot(fpr, tpr, label='ROC curve (area = %.2f)'%auc)
plt.legend()
plt.title('ROC curve')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.grid(True)
plt.show()

# accuracy, precisionを計算
acc = metrics.accuracy_score(np.asarray(test["y"]), np.round(y_pred))
precision = metrics.precision_score(np.asarray(test["y"]), np.round(y_pred))
print("accuracy", acc)
print("precision", precision)

# 混同行列をプロット
y_pred = np.round(y_pred)
cm = metrics.confusion_matrix(np.asarray(test["y"]), np.where(y_pred < 0.5, 0, 1))
cmp = metrics.ConfusionMatrixDisplay(cm, display_labels=[0,1])
cmp.plot(cmap=plt.cm.Blues)
plt.show()

出力

売買シミュレーション

今回作成した予測モデルを用いてトヨタ株の売買シミュレーションを行う。
シミュレーション方法は参考文献に従って、以下の通りとする。

最初の予算は100万円

売買の判断は毎日行う。

手元に株を持っていない場合

翌日の終値が当日の終値より「上がる」と予測された場合、

翌日の始値で手元の資金が許す限り株を買う。

翌日の終値が当日の終値より「下がる」と予測された場合、

株を買わず現金のままで資金を持ち続ける。

手元に株を持っている場合

翌日の終値が当日の終値より「上がる」と予測された場合、

そのまま株を持ち続ける。

翌日の終値が当日の終値より「下がる」と予測された場合、

翌日の始値で手元の株を全て売却する。

Python3

sim = test[["toyota_終値", "toyota_始値"]]
sim["y_pred"] = y_pred

money = 1_000_000
stock = 0
pred = 0
history = []

# シミュレーションを実施
for _, row in sim.iterrows():
  if pred:
    if stock:
      # 上がると予測されて株を買っているとき
      pass
    else:
      # 上がると予測されて株を買っていないとき
      stock = money // row["toyota_始値"]
      money %= row["toyota_始値"]
  else:
    if stock:
      # 下がると予測されて株を買っているとき
      money += row["toyota_始値"] * stock
      stock = 0
    else:
      # 下がると予測されて株を買ってないとき
      pass
  pred = row["y_pred"]
  history.append(money + row["toyota_始値"] * stock)

# シミュレーション結果を出力
fig = plt.figure()

ax1 = fig.subplots()
ax2 = ax1.twinx()

ax1.plot(sim.index, history, color="orange", label="total assets", linewidth=1)
ax2.plot(sim.index, sim["toyota_終値"].values, color="blue", label="stock prices", linewidth=1)
h1, l1 = ax1.get_legend_handles_labels()
h2, l2 = ax2.get_legend_handles_labels()
ax1.legend(h1 + h2, l1 + l2)
ax1.set_ylabel("total assets")
ax1.grid(True)
ax2.set_ylabel("stock prices")
plt.setp(ax1.get_xticklabels(), rotation=45)
plt.tight_layout()
plt.show()

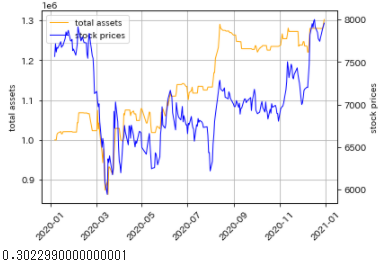
print(history[-1] / 1_000_000 - 1)

出力

(実際には手数料や税金が引かれるため、この金額よりは少なくなります。)

(追記)

予測モデルを使わなかった場合のシミュレーションを行い比較してみた。

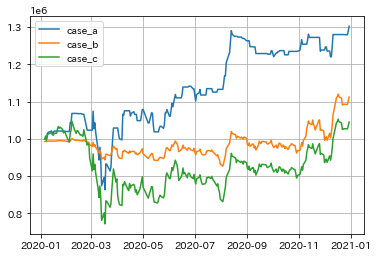
case_a : 前述の予測モデル及びシミュレーション方法
case_b : 毎月月初の始値を定額で購入（合計100万円分）
case_c : 年始の始値で100万円分購入した後に放置

結果

最終的な利益はcase_aが最も高くなった。
しかし、2020年3月ごろの暴落時にはcase_bの総資産額が最も多くなった。そのため、暴落に備えてなるべくリスクを減らしたい場合は、予測モデルは使わずに毎月定額で買うことがよいと考えられる。

(追記終了)

今後のやりたいこと

シミュレーションに空売りを取り入れて、株価が下がる際にも資産を増やせるようにする
ネット証券口座と連携して自動売買を行う、実運用に向けた取り組み
モデルの予測精度向上

実運用をするにあたって重大な課題点

圧倒的資金不足

年利30%とはいえ、元手が1万円とかだと、3000円の利益にしかならない。

最後に

今回はLightGBMを用いた株価の値動き予測を行いました。
シミュレーションの結果、手数料、税金を考慮しない場合年利30%のプラスとなりました。
今回はAI部分のみの作成で、肝心の自動売買のシステムは作成していないので、またの機会に記事にしようと考えております。

想定以上に良い結果となって、どこかに間違いがあるような気がするので、コメントでの指摘をお待ちしています。

年利30%超え！！！！！LightGBMを用いたトヨタ株自動売買シミュレーション

TL;DR

背景

実験環境

使用データ

必要なライブラリのimport

データの読み込み

特徴量の作成

訓練データの作成

予測を実行

モデルの評価

売買シミュレーション

今後のやりたいこと

実運用をするにあたって重大な課題点

最後に