機械学習入門：動かして学ぶ、機械学習のキソ(回帰問題編) #機械学習

※本記事はOracleの下記Meetup「Oracle Big Data Jam Session」で実施予定だった内容です。本会が中止になりましたので、こちらの記事にて代用させていただきます。

※本記事のセミナー内容は以下の動画でも公開しておりますのでよろしければご参照ください。

本記事の対象者

これから機械学習を利用した開発をしていきたい方
機械学習のトレンド技術を知りたい方
なるべく初歩的な内容から学習したい方

そもそも機械学習とは

皆様は「風が吹けば桶屋が儲かる」という江戸時代からあることわざをご存知だと思います。風が吹けば寒く感じ、多くの人が風呂屋にいくために桶を買うので桶屋が儲かるという意味かと思いこんでいましたが、実際は違う意味だそうですね。(wikipedia - 風が吹けば桶屋が儲かる)

いずれにせよ、このことわざは、ある事象(風が吹くという事象)と一見まったく関係がないと思われる他の事象(桶がたくさん売れるという事象)に、実は何らかの因果関係があるという教訓を表したものです。機械学習とはまさに、データからこの因果関係を見つけるための統計処理と言っていいでしょう。

このことわざになぞらえて、桶屋の売上を機械学習で予測しようとすると、以下のように、「桶屋の売り上げ」と「風速」というデータが必要になります。

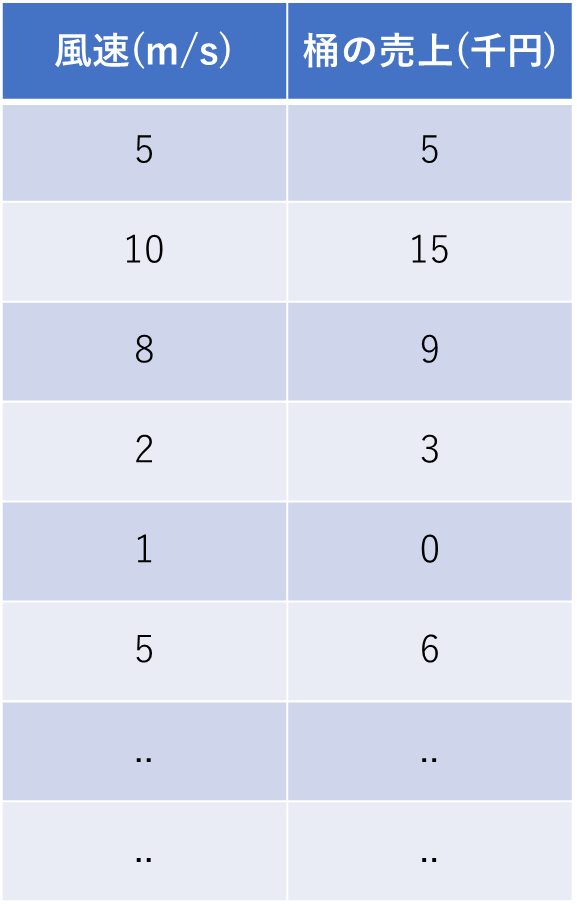
このデータをチャートにしたとき、仮に以下のような分布になった場合、「桶屋の売り上げ」と「風速」に何か法則(因果関係)が見えてきそうですよね？

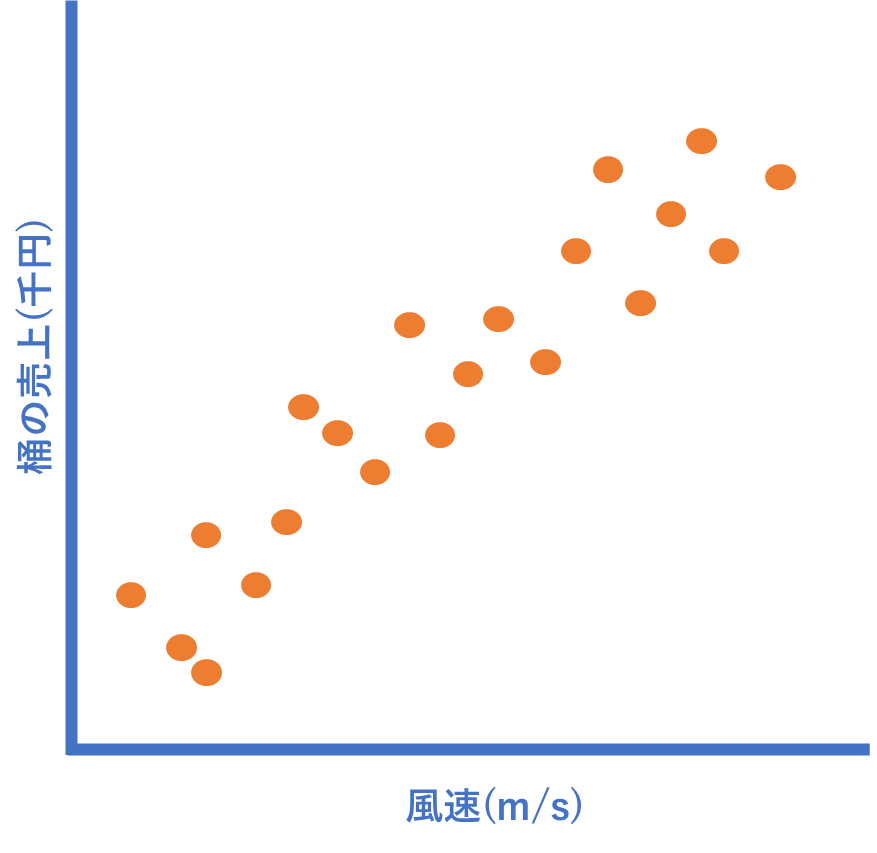
そうです、以下のような感じで、おおよその直線が引けることに気付きます。仮にこの直線を表す関数がy=x+1となった場合、その日の「風速」さえわかれば、「売り上げ」が予測できることになります。

機械学習とはまさに、大量のデータからこのような法則(関数)を見つけ出す統計処理と言えます。ただし、実ビジネスで発生するデータは上記のように都合よくは分布してくれませんよね。また、関係する事象も「風速」一つだけということはあり得ません。そのような状況でも、あらゆる分析ができるように多種多様なアルゴリズムや学習手法があります。沢山のアルゴリズムがリストされている下記のような資料や記事などをよく見かけますが、上述した理由で昔からたくさんの手法が研究・開発されているのです。

基本は「回帰」と「分類」

世の中には沢山のアルゴリズムや学習手法があります。特に非構造化データ(画像データ、音声データ、自然言語)などを使った深層学習は非常に興味深いのですが、実ビジネスで考えると、「回帰問題と分類問題の解き方をいろんなアルゴリズムで試行錯誤できるようになる」が基本です。まずは回帰と分類さえマスターしておけば、皆さまの普段のお仕事に応用できる機会は沢山あるからです。世の中の機械学習のニーズのかなりの範囲を、この2つのパターンで満たせるといっても過言ではありません。それくらい、回帰と分類は適用範囲が広いのです。

回帰とは、先ほどのことわざの例でいうと「桶屋の売り上げ」、つまり売り上げという数値(連続値)を予測するというものです。この後、ご紹介する回帰のコードでは、ある条件下にある「不動産の価格」、つまり価格という連続値を予想するというものになります。

そして分類とは、ある条件下にあるものを「複数のカテゴリに分類する」というものです。この分類タイプのコードも下記記事でご紹介していますので是非ご参照ください。ワインの成分データを集めた情報から、ある条件下(タンニンの含有率、アルコール度数など)のワインの品質が「good」なのか、「better」なのか、「best」なのかの3つのどれかに分類するという分析シナリオです。

※もし、画像データ、音声データ、自然言語の機械学習に興味がある方は過去に実施した以下のセッションをご参照ください。

教師あり学習と教師なし学習

回帰も分類も、一体何を拠り所に、学習処理をするのでしょうか。それに関係するのが「教師あり学習」と「教師なし学習」という学習手法です。機械学習のコードを書いたことがない方でも、これは知っているという方は多いのではないでしょうか。

特にわかりやすいのは「教師あり学習」です。教師あり学習では、集めたデータに「答え」、つまり過去の桶の売り上げ実績が入っています。従って、答えである「桶の売り上げ」を拠り所に、「風速」との関係性を学習します。「答え」を教えてくれる教師がいる状態のデータということで教師あり学習という名前がついています。これは「風速」以外に沢山の条件がある場合でも同じです。そして、この「答え」に相当するデータを「教師データ」と言ったり、「正解ラベル」と言ったりします。

ということは、「教師なし学習」は上記の反対で「答え」のデータがない(というより不要)というタイプの学習手法です。例えば、日本人の身長と体重のデータが1000人分あるとします(下図)。このデータを利用して、ある服飾メーカーがTシャツを作る際に、S、M、Lのサイズ感をどのように決定するかを考えてみましょう。機械学習にあてはめて考えると、この1000人を体格の近しいと思われる3つのグループに分けるということになります(更に下の図)。この場合、あるアルゴリズムに基づいて、データの特徴から単にグルーピングをするだけですから、「答え」は不要ということになり、「正解ラベル」不要の「教師なし学習」ということになります。

ここまで理解できれば、機械学習の基本コンセプトはもうマスターしたと思って問題ありません。後はさっさとコードを書いて動かすことを繰り返すだけです。その際、僕のオススメは「余計な処理が入っていない極めてシンプルなコードを学習する」ということに尽きます。最近の機械学習ライブラリはどれも非常に秀逸で、ライブラリの抽象度も高いため、かなり簡単に機械学習のコードが書けるようになっています。が、それを差し引いても、ことはじめはこの上なくシンプルなコードを扱うことをオススメします。機械学習はただでさえ専門用語が沢山でてきて難解に感じます。はじめはいろんなことに手を出さずに、セオリー通りのワークフローで最低限のコードを扱い、「機械学習のコードの基本的な骨格」をぼんやりとでも理解することにフォーカスすることが重要だと思うからです。何度かコードを書くと、「なるほど、だいたいどれもやっていることは同じなんだな」と感じることが多くなってくると思います。そう感じたときに、これまでやってこなかった追加のコードを入れてみるなど試行錯誤するのも一興だと思います。機械学習は追及しだすといろんなことをやりたくなってしまいがちです。またそれら知的欲求を掻き立てるように、興味深い沢山のライブラリがリリースされているのですが、ここはグッとこらえて「なにごともHello Worldから」です。

ワークフロー

機械学習のワークフローというのは、上述した「なるほど、だいたいどれもやっていることは同じなんだな」という部分になります。具体的に書き出すと以下のような項目です。

データのロード
データの把握、前処理
学習
評価

実際のコードを動かす前に、各フローの概要を把握しておきましょう。

データのロード
機械学習にかけるデータを読み込む処理です。本記事では、機械学習のライブラリであるscikit-learnに付属しているデータセットを使いますのでデータのロードは、たった一行で完了です。しかし、実際には、データレイクやデータベースからデータを読み込むなど、データストアには多数の種類があります。また、リアルタイム分析のシステムではpub/subのシステムからデータをとったり、ツイッターなどサービスのAPIを利用してデータをとりにいくパターンなど、その手法は様々です。
データの把握、前処理
集めたデータの内容を把握して、分析シナリオに合わせたデータの加工が必須となります。各特徴量が連続値なのかカテゴリカルなのか、各特徴量の相関関係はどの程度か、学習にかける特徴量は足りているのか、足りていなければ新たにどのような特徴量を作るのか、欠損値はないか、どのように値が分布しているか、などなど、このフェーズではやることがたくさんあります。また、正解ラベルが必要な分析シナリオでは、正解ラベルをどう集めるかといった大きな問題にあたることもあります。機械学習の中でも最も重要なパートです。ここでの作業の質がそのまま予測モデルの精度に直接的に影響してきます。
学習
前処理が完了したデータを統計処理にかけて学習させ、予測モデルを構築するフェーズです。沢山のアルゴリズムから最適なものを選ぶ必要があります。また各アルゴリズムにはパイパーパラメータと呼んでいるチューニング可能なパラメータがあり、パターン数を考えると膨大な数になります。が、昨今はどのライブラリもAutoMLの機能が豊富で、アルゴリズムもハイパーパラメータも最適なものを自動的に選択してくれますので、概要を理解していれば十分です。このフェーズでは難解なアルゴリズム名が多々でてくるので、非常に難しいパートのように感じますが、実は各アルゴリズムの適用パターンはおおよそ決まっています。また各アルゴリズムは一度理解してしまうと、その内容が大幅に変わることはあまりありませんので、最初のハードルを越えてしまうと、あとはお決まり流れのコードを書くという作業になります。また、このように定型化できる部分をなるべくコンピュータにやらせて自動化してしまうAutoMLの仕組みは今後もますますエンハンスされるでしょう。
予測モデルの評価
学習して予測モデルが構築されれば、機械学習は完了！とはなりません。実際に構築したモデルの精度を評価し、リリースしてもよいかどうかを判断します。精度の評価は、「メトリック」と呼んでいる値を算出し、その値によって判断します。回帰や分類など、それぞれのタイプに応じたメトリックが存在し、その算出方法も決まっています。精度が低い場合は、前のフェーズに戻り、データの前処理内容を見直したり、アルゴリズムやハイパーパラメータを変えたり、ときにはビジネスゴールに応じて分析シナリオそのものを変更する必要もあります。このような試行錯誤を繰り返し、最終的に精度を確保したモデルを構築します。

※場合によっては、この後に「予測モデルの解釈」というフェーズがあります。これは、出来上がった予測モデルを理解するために必要なフェーズです。開発者が予測モデルを理解することで、そのモデルに欠陥やバグがあった場合に気付きやすくなります。また、ある予測を行った場合に、なぜそのような予測結果になったかを説明することができるようになります。これは非常に重要なことで、昨今、認知が広がっている分野です。機械学習は目的ではなく手段です。その予測結果をもとに何らかの業務的なアクションを行うことになります。その意思決定の理由が、「なんか機械学習にかけたら、こんな結果になったので、とりあえずこれでやってみます。」で通る企業はないからです。

分析シナリオ

サンプルコードを動かし、その内容つまり、分析シナリオを理解するには、データセットの内容に着目することが一番重要です。今回の回帰分析では「The Boston house-price data」と呼ばれる有名なデータセットを使います。このデータは米国国税調査局が収集した情報をベースに作成されたデータセットです。ボストンの町ごとの「犯罪率」や「非小売業の割合」など、全部で14の属性(列)を持ったデータセットになっています。本サンプルコードでは、青色の13個の属性と赤色の1個の属性の関連性を学習し、予測モデルを構築します。すなわち、その町の13個の属性から、赤色の属性、つまり住宅価格を予測するモデルを構築するというものです。

各列の概要は以下の通りです。

CRIM：犯罪率
ZN：広い家の割合(25,000平方フィートを超える住宅地の割合)
INDUS：非小売業の割合
CHAS：チャールズ川隣接状況(隣接の場合：1、隣接していない場合：0）
NOX：一酸化窒素濃度
RM：平均部屋数
AGE：築古の割合(1940年より前に建てられた持ち家の割合)
DIS：主要施設への距離(ボストン雇用センターまでの加重距離)
RAD：主要高速道路へのアクセス性指数
TAX：固定資産税率(10,000ドル当たり)
PTRATIO：生徒と先生の比率
LSTAT：低所得者人口の割合
MEDV：住宅価格(1000ドル単位の中央値)

それでは、実際にプログラムを動かしてみましょう。コードを動かす環境としてはPython、機械学習ライブラリはscikit-learnを使いたいと思います。ご自身のラップトップにインストールしたPythonでも動作しますが、Oracle Cloudに Data Science Serviceと呼んでいる機械学習のクラウドサービスがあり、そちらをご利用いただくと、非常に簡単に環境の構築が可能です。

※もしData Science Serviceを使ってみようと思われる方は、以下のビデオで簡単に同サービスのプロビジョニングが可能です。

環境がセットアップできたら、さっそくコードを書いてみましょう。
(本サンプルコードはJupyter Notebook形式でOracle Japan公式リポジトリに掲載しております。)
まず初めに必要なライブラリをimportします。機械学習では集めたデータを配列に入れ込んで、データの操作や処理を行います。そのため、多次元配列用のライブラリやデータ操作のためのライブラリ(numpy、pandas)が必要になります。また、データを視覚化しチャートとして表示するためのライブラリ(seaborn、maploptlib)をインポートします。

import numpy as np
import matplotlib.pyplot as plt 

import pandas as pd  
import seaborn as sns 

%matplotlib inline

次に、データのロードです。上述したボストンの不動産価格情報のデータセットはscikit-learnに含まれていますので、以下のようなコードで簡単にデータのロードができます。

from sklearn.datasets import load_boston
boston_dataset = load_boston()

データ操作の処理をするために、boston_datasetをpandasのデータフレームに変換し、head()でデータを確認してみます。

boston = pd.DataFrame(boston_dataset.data, columns=boston_dataset.feature_names)
boston.head()

予測対象の不動産価格情報(MEDV)の列がありませんね。これが正解ラベルになりますから、このデータフレームにMEDVの列を追加する処理を下記のように行います。このようにデータ処理を簡単に行えるようにするために、学習データをpandasのデータフレームに変換しておくということになります。

boston['MEDV'] = boston_dataset.target
boston.head()

上記のように、正解ラベルである、MEDVの列が追加されていることがわかります。ここから簡単なデータの確認作業をしてみましょう。まず初めに行うべきは、データの欠落があるかどうかの確認です。下記のようにisnull()で簡単に確認できます。

boston.isnull().sum()

全てゼロなので、欠損値はないということが確認できました。
ここからより詳しく、データを把握してゆきます。データの把握と一言でいってもその作業は様々です。しかし、もっとも重要なことは、そのデータの「分布」を把握するということです。ですので、このデータセットで非常に重要な特徴量であるMEDV(不動産価格)の分布を、先にimportしたseabornでチャート化してみましょう。

sns.set(rc={'figure.figsize':(11.7,8.27)})
sns.distplot(boston['MEDV'], bins=30)
plt.show()

まず、外れ値がほとんどないということ、そして、値が明らかに正規分布であることがわかります。正規分布とは連続値のデータが平均値あたりに集中し、最小値、最大値に近づくにつれて、減少するような分布のことを言います。このような偏りの少ないデータはそのまま機械学習にかけやすいデータと言えるでしょう。

そして、次に重要な確認が、各特徴量の相関関係になります。これも下記のように、seabornを使ってヒートマップ形式で表示することにより、一目で相関関係の強さが確認できます。

correlation_matrix = boston.corr().round(2)
sns.heatmap(data=correlation_matrix, annot=True)

縦軸と横軸に全ての特徴量がプロットされ、その相関関係の強さを色の具合によって直感的に把握することができます。相関関係は-1から1の間の値で表示され、ゼロから-1に近づくにつれて、負の相関関係が強く、ゼロから1に近づくにつれて、正の相関関係が強いということになります。相関関係はその計算式から、以下のような傾向を把握するために、正と負があります。

・ある特徴量が大きくなれば、もう一つの特徴量も大きくなる場合、相関係数は正で表される
・ある特徴量が大きくなれば、もう一つの特徴量は小さくなる場合、相関係数は負で表される

今回の回帰分析では線形回帰と呼んでいるアルゴリズムを利用します。線形回帰では、予測対象の特徴量を目的変数、その他の特徴量を説明変数と呼びます。目的変数と相関関係の強い説明変数を使って機械学習を行うと精度の高い予測モデルが作れそうだということは直感的にわかりますよね。
また、説明変数同士の相関関係が高い場合、多重共線性と呼んでいる症状が発生し、正確な精度を把握することができなくなるため、特に回帰問題では注意が必要です。
したがって、上述したヒートマップから、相関関係をちゃんと把握し、学習に使う特徴量を選別することが重要になります。(※実際の分析の現場では、ここは試行錯誤を繰り返したり、AutoMLの機能で対応したりします)

このbostonのデータセットのヒートマップを具体的に見てみると、

特徴量DISとAGEは0.75、RADとTAXは0.91という強い相関関係にあるため、説明変数には使えなさそう
目的変数であるMEDV(不動産価格)と相関の強い、LSTAT(低所得者人口の割合)と、RM(平均部屋数)は説明変数として使えそう

という状況なので、今回はシンプルにこのLSTATとRMを説明変数の候補にして学習してみたいと思います。学習の前に、念のため、説明変数の候補であるLSTAT、RMと、目的変数であるMEDVをチャートにして見てみましょう。

plt.figure(figsize=(20, 5))

features = ['LSTAT', 'RM']
target = boston['MEDV']

for i, col in enumerate(features):
    plt.subplot(1, len(features) , i+1)
    x = boston[col]
    y = target
    plt.scatter(x, y, marker='o')
    plt.title(col)
    plt.xlabel(col)
    plt.ylabel('MEDV')

おぼろげに以下のような傾向があるように見えますよね。

LSTATが大きくなるにつれて、MEDVは小さくなる(つまり、低所得者の割合が増えるにつれて、その所有者の不動産価格は低い)
RMが大きくなるにつれて、MEDVは大きくなる(つまり、部屋数が増えるにつれて、不動産価格は高くなる)

という感じで、感覚的に納得感がある分布で、このデータセットは非常にわかりやすいですね。

説明変数が決まれば、次は学習のフェーズです。下記のコードで、この2つの説明変数からXという名前で説明変数のみのデータフレームを作ります。そしてYという名前で目的変数だけのデータフレームを作ります。

X = pd.DataFrame(np.c_[boston['LSTAT'], boston['RM']], columns = ['LSTAT','RM'])
Y = boston['MEDV']

そして、作成したデータフレームを、次のコードで学習用データ(X_train, Y_train)と評価用データ(X_test, Y_test)に分割します。評価用が0.2とあり、これはデータ量の20%を意味します。つまり、80%のデータで学習し、作った予測モデルを20%のデータで評価するということになります。

from sklearn.model_selection import train_test_split

X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.2, random_state=5)
print(X_train.shape)
print(X_test.shape)
print(Y_train.shape)
print(Y_test.shape)

上記のような出力となり、これは

説明変数の学習用データ X_trainが404行、2列(LSTATとRM)
説明変数の評価用データ X_testが102行、2列(LSTATとRM)
目的変数の学習用データ Y_trainが404行、1列(MEDV)
目的変数の評価用データ Y_testが102行、1列(MEDV)

ということを意味しています。
できあがったデータを学習にかけます。学習に使うアルゴリズムは線形回帰(LinearRegression)と呼んでいるものです。LinearRegression()から予測モデルlin_modelを作成し、fit関数で学習をしています。もちろん、説明変数のデータフレームであるX_trainと目的変数のY_trainの関係性を学習するためにこの2つのデータフレームがfit関数の引数となっていることが下記コードからわかります。

from sklearn.linear_model import LinearRegression

lin_model = LinearRegression()
lin_model.fit(X_train, Y_train)

これで学習が完了し、予測モデルが構築できましたので、実際に予測処理を行ってみたいと思います。予測するデータは学習時に利用しなかった X_test から一行抜き出して、そのデータで予測をします。

X_pred = X_test.iloc[0:1]
print(X_pred)

このデータから不動産価格を予測させる処理を行います。LSTATが3.21、RMが8.04のときに不動産の価格MEDVがいくつになるのかを予測します。予測処理を行う前に、正解を確認しておきましょう。

Y_pred = Y_test.iloc[0:1]
print(Y_pred)

上記から、実際の正解はMEDV=37.6ということがわかります。この値に近しい値が予測できるかどうかが、構築した予測モデルの精度ということになります。予測処理をする場合はpredict関数を使います。

lin_model.predict(X_pred)

上記の通り、37.38という値が予測できました。感覚的には、正解の37.6に比較的近しい値だと思いますが、これはたまたまかもしれません。従って、このモデルをちゃんと評価して、モデルの精度を数値化する必要がでてきます。

回帰モデルを評価する際に、最低確認しなければいけない指標は「二乗平均誤差(RMSE)」や決定係数(R2)と呼んでいるものを使います。難しそうな名前ですが、評価用データ全てに対して、予測値と、実際の正解データの乖離を計算し、どれくらいの誤差があるかというところからモデルの精度をパーセンテージで確認する手法です。

from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score

y_train_predict = lin_model.predict(X_train)
rmse = (np.sqrt(mean_squared_error(Y_train, y_train_predict)))
r2 = r2_score(Y_train, y_train_predict)

print("The model performance for training set")
print("--------------------------------------")
print('RMSE is {}'.format(rmse))
print('R2 score is {}'.format(r2))
print("\n")

y_test_predict = lin_model.predict(X_test)
rmse = (np.sqrt(mean_squared_error(Y_test, y_test_predict)))
r2 = r2_score(Y_test, y_test_predict)

print("The model performance for testing set")
print("--------------------------------------")
print('RMSE is {}'.format(rmse))
print('R2 score is {}'.format(r2))

上記では、テストデータに対する評価の結果としてRMSE=5.137、R2スコアは0.662という値になりました。それほど高い値ではないので、このままでリリースするのはさすがに難しいですね。このデータセット以外のデータを追加し、説明変数を増やす必要がありそう、というような感じで、データ収集のフェーズにもどって、説明変数の設計をやり直すなど、実際の分析の現場では試行錯誤を繰り返すということになります。

MLOpsに取り組もう

上述した内容は予測モデルを構築する処理にフォーカスしたものです。予測モデルが構築できればそれですべてが完了ということにはなりません。データにはトレンドがある場合が多く、一度作ったモデルを未来永劫使うということはありません。データのトレンドが変わればまた新しいモデルを作り直す必要があり、結局はこれまで説明してきた内容を何度も繰り返す運用になります。この運用をできるだけ標準化していこうという考え方がMLOpsです。MLOpsではkubeflowやmlflowといったツールがよく使われますが、mlflowについては過去の下記セッションで取り上げていますので是非ご参考にされてください。

さいごに

今回は回帰問題タイプのコードを見てきました。これらは最低限理解しなければいけないHello World的なコードであり、機械学習のコードの骨格のようなものです。あとは、各フェーズで、更に様々なライブラリや関数を用いて、もっと詳細な、そして多岐にわたる処理や確認などを行い、この骨格に、肉付けをしてゆきます。

昨今は自分でコードを書かなくても、GUIで簡単に機械学習を実行できるツールが沢山のベンダーから提供されています。そうだとしても、自分でコードを書くということも併せてせてやっておくといいことがあります。

まず、常に最先端のアルゴリズム、学習手法などが利用できるGUIベースのツールは恐らくないと思います。最先端のライブラリは大抵PythonやRのライブラリ形態で提供され、GUIベースのツールがそれらをサポートするのはそのずっと後です。ですので最先端の手法を取り入れたいという場合はコーディングベースが最適です。

また、GUIベースのツールは精度が出なかったらそれまで、という感じで行き詰る可能性もあります。当たり前ですが、GUIとして実装されている機能以外は使えませんので、帯に短しという状況になる可能性があるということが言えます。一行一行自分でコードを書きながら試行錯誤したり、GUIツールではできない詳細の把握はコーディングベースの強みです。

そして、いくらGUIベースで簡単だと言っても、何も知らない状態では利用が難しい場合があります。メニューやドロップダウンリストから何を選べばよいのか、チューニングのオプションなどがある場合に、各項目のチューニング内容や、どういう値にするか、などはコーディングベースで深く理解していると、より効果的かと思います。

とはいえ、GUIツールを使うメリットは、あまり詳しくなくても機械学習ができたり、くわしくても、コードを書く工数が大幅に削減できますので、適材適所で是非取り入れていきたいところですね。